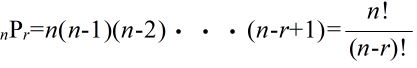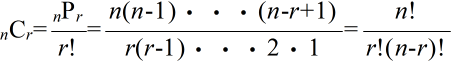- システム工学とは
- システムとは,
- 様々な要素の集まりからなり,それらの要素が互いに関連しあい,全体として,ある目的を果たすための機能を有するもの
- といえます.「要素が互いに関連しあい,全体として,ある目的を果たすための機能を有する」という点が特に重要です.少なくとも,単に要素が集まっているだけではシステムとはいえないからです.従って,システムにおいては,個々の要素技術と共に,それらの要素の組み合わせ技術も非常に重要となります.例えば,単に最適な要素を組み合わせただけでは,全体として最適なシステムになるとは限りません.組み合わせたものを全体として評価し,その結果を各要素に反映させることができるような技術者が必要です.そのような技術者の基礎となるのが,システム工学(SE : Systems Engineering, System Engineering)です.そして,システム工学的な知識に基づき,システムの解析,設計,運用などに携わる技術者がシステムエンジニアであると言えます.
- 人口の増加や,生産技術,科学技術,情報伝達・処理手段等の進歩等により,システムが大規模かつ複雑になり,単に要素技術だけでなく,それらをまとめる技術-システム工学-がますます重要になっています.そのため,要素技術や科学技術一般に関する知識と共に,モデリング,スケジュール,最適化,制御等,システム工学固有の技術・知識を持った人に対する必要性は今後ともさらに高まっていくものと思われます.勿論,ここで言うシステムとは情報システム( IT システム,コンピュータシステム)だけを表しているわけではありません.ここでは,システムエンジニアという言葉を,情報システムを含む一般的なシステムの解析,設計,運用などに携わる技術者を表す言葉として使用します.「システムエンジニアの基礎知識」では,そのような技術者が身につけて欲しい知識について記述していきます.
- システム工学と似た分野としてオペレーションズ・リサーチ( OR : Operations Research )という分野が存在します.非常に似た分野ですが,
- システム工学はハードウェア,OR はソフトウェアに重点を置いている.
- システム工学は新しいシステムの設計・製造,OR は既存のシステムを如何に運用するかといった点に重点を置いている.
- といった点で異なっているといえます.しかし,製造したシステムをどのように運用するべきかといった問題は,システム工学にとっても非常に重要です.そのような意味で,OR はシステム工学に含まれるといっても良いかもしれません.「システムエンジニアの基礎知識」においては,そのような立場で記述しています.
- 情報システム
- システムの一つとして,情報の収集,処理,伝達等を目的としたシステム-情報システム( IT システム,コンピュータシステム)-が存在します.このようなシステムの解析,設計,運用に携わるシステムエンジニアを情報システムエンジニア( IT システムエンジニア)と呼ぶことにします.日本において,職種の一つとして使用されている SE(システムエンジニア)は,一般的には,プログラマ,組み込みエンジニア,サポートエンジニアなど,IT 関係の要素業務をこなす技術者を指す場合がほとんどです.言葉として,電気技術者が電気工学に対応するように,システムエンジニアは,システム工学( Systems Engineering, System Engineering )という言葉に対応しますので,システム工学的な知識・考え方を身につけた技術者であるように感じられますが,必ずしもそのようにはなっていません.明らかに,SE は,単なる職種を表した言葉であり,ここで述べているシステムエンジニアとは異なります(以後,SE と記述した場合は職種を表すものとする).しかし,情報システムもシステムの一種です.必ず,システムエンジニアが必要です.実際,SE の中には,情報システムエンジニア的な業務に携わっている人も多いと思います.システム工学に関わる知識を身につけ,その重要性を十分認識し,SE という言葉にふさわしい真のシステムエンジニアを目指してもらいたいと思います.「システムエンジニアの基礎知識」を記述した目的の一つはここにあります.
- システム工学の手順
- システム工学の手順を簡単に述べれば以下のようになります.その各段階で,ここで述べるシステムエンジニアの基礎知識が必要になってくると思います.
- システムの目的 システムの目的・目標を明確にします.単に,与えられた要求を満たすシステムを作成するだけではなく,「システムの目的は何か」,「なぜ必要なのか」,「業務記善など,他の方法で実行できないか」,「他の分野(システム)との関係は?」など,より踏み込んだ検討をする必要があります.ある意味で,システムエンジニアにとって,最も重要な過程であるといえます.場合によっては,この過程において,システムの開発自体を行わないといった結果に至ることもあり得ます.
- システム分析 構成すべきシステムに対して,システムの目的に基づき,運用,効率,コスト,品質,信頼性分析等を行います.場合によっては,目的自身を再検討する場合もあり得ます.
- システム計画 システムが完成するまでの日程計画を作成します.このとき,予算(コスト)や信頼性などの管理計画も作ります.
- システム設計 最適なシステムを目指し,システム全体,サブシステム,構成部品等の設計を行います.
- システム製造 システム設計にしたがって,実際にハードウェア,ソフトウェアを製造します.
- システム運用 システムが本来の目的を達成できるように保守,整備を行います.
- ステムエンジニアに必要な知識
- SE に必要な知識としてコミュニケーション能力が良くあげられます.また,複数の人間でシステムを作り上げる際には,管理能力も当然必要になります.これらの能力は,一般的なシステムエンジニアに対しても当然要求される能力ですが,ここでは,これらの社会人基礎力的な能力については触れません.
- SE の仕事内容や必要な知識に関して,インターネットなどに書かれているものを読むと非常に気になる点があります.SE の仕事は,顧客の要求を聞き,それを満足するコンピュータシステムを構築することであるといった内容がほとんどです.コンピュータ等の構成が決まっていれば,これでは,単に,「顧客が要求する入出力を行うプログラム」を書くプログラマに過ぎません.しかし,先に述べたように,情報システムもシステムの一種です.必ず,システムエンジニアが必要です.システムエンジニアにとって最も重要なのは,システム工学の手順の中に記述した「システムの目的」を明確にすることですが,そのような記述がほとんどありません.顧客の業務内容,システム利用者の要求・使用方法,他のシステムとの関係等を分析し,その中で顧客やシステム利用者にとって最適なコンピュータシステムを提案できるようでなければなりません.また,場合によっては,顧客の業務内容の他の部分を改善することによって,顧客が要求するシステムを必要としない場合もあるかもしれません.単に顧客の要求を聞き,それを実現するだけでなく,より踏み込んだ検討が必要です.そのようなことができなければ,とてもシステムエンジニアとは言えません.
- 情報システムを例として,もう少し,システムエンジニアの必要性について述べていきます.現在,業務ごとに,多くのパッケージソフトが販売されています.従って,組織全体の情報システムのあり方等を検討するシステムエンジニアが存在しなくても,組織内のある分野で必要な処理を行うパッケージソフトを導入し,また,別の分野ではその分野で必要な別のパッケージソフトを導入するといったことを繰り返して,全体の情報システムを構築することも可能です.要するに,各分野にとって最適なサブシステムの集まりとして,全体システムを構築する方法です.一つのサブシステムに問題が生じても他のサブシステムに影響を与えにくい,情報の漏洩も一部のサブシステム内にとどまる可能性が高いなどの利点もありますが,一般には,使いやすさ,マンパワーを含めたりソースの無駄遣い等の問題が発生する場合が多いと思います.その一つの例が官公庁のシステムです.ある処理を行うために,複数の窓口を訪れるなどという経験は誰にでもあるかと思います.極端な例かもしれませんが,"父親が亡くなった"ような場合について考えてみてください.官公庁の情報システムが統合されていれば,死亡届と相続者情報を一つの窓口に提出すれば,ほとんどすべての処理が終わるはずです.実際には,市役所の複数の窓口,年金事務所,法務局など,複数の場所へ,同じような書類を用意して出向かざるを得ません.我々の手間も必要ですし,さらに,それらの書類を処理する公務員も必要(税金が高くなる)です.確かに,個人番号制度に対する反対の理由として挙げられているセキュリティ上の問題もありますが,全体システムを考慮した優れたシステムが存在すれば,我々の手間と公務員の削減には大きな力となるはずです.
- 「システムエンジニアの基礎知識」は,Ⅱ部構成になっています.システムエンジニアは,システム工学的な考え方と共に,システムの分析,設計,運用を行うための手法に対する知識も必要です.直接自分で行うことはなくても,どのような手法が存在するか程度の知識は必要だと思います.第 Ⅱ 部では,そのような手法について簡単に述べています.実際の問題においては,システムが対象とする各分野に関する知識も必要となりますが,ここでは触れません.第 Ⅱ 部で扱う各手法をより深く知ろうとすれば,どうしても数学的な知識が必要になります,第 Ⅰ 部は,そのような数学に関する記述です.特に,線形代数,微分積分,確率統計は,様々な分野の基礎となっていますので,システムエンジニアだけではなく,一般の技術者にも身につけてもらいたいと思います.ただし,「代数系」,「ブール代数」,及び,「記号論理学」に関しては,第 Ⅱ 部を理解する上で直接必要とすることはないと思われますので,読み飛ばしてもらっても構いません.なお,第 Ⅰ 部の「基礎数学」は,小学校から高校までに学んだ数学を思い出し,理解し治してもらうための部分になっています.その内容は,「基礎数学」とほとんど同じです(「基礎数学」内に記述がある「集合」,「空間図形」,「微分・積分」,「確率」は除く)が,演習問題は含まれていません.
- また,現在では,多くのシステムにおいて,コンピュータが主要な役割を果たしています.従って,どのような分野であれ,コンピュータ関連の知識も多かれ少なかれ必要になってくる場合が多いと思います.特に,コンピュータソフトウェアの開発が大きな部分を占めるようなシステムにおいては,少なくとも一つ以上の言語に対する十分なプログラミング技術を持っている必要があるのではないでしょうか.なぜなら,目的とすることをソフトウェアで実現可能か,どの程度の困難さが伴うのか,どのようにすれば最適なプログラムかを書けるのか,などといった判断は,そのシステムの開発に携わっている人自身が判断するのが最も好ましいからです.それが可能であるためには,判断者自身が十分なプログラミング能力を持っている必要があります.コンピュータ関連の知識やプログラミング技術については触れませんが,本文には,各手法に対する C/C++ と Java (一部に,JavaScript を含む)によるプログラム例をできるだけ添付すると共に,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例も示してしていくつもりです.これらのプログラミング言語に関しては,「C/C++ 言語」,「 Java と C/C++ 」,「 JavaScript と C/C++」,「 PHP と C/C++」,「Python と C/C++ 」,「Ruby と C/C++ 」,「プログラミング言語の落とし穴」などを参考にして下さい.
- 基礎数学
- 中学や高校で学んだ数学に関しては,あえて触れる必要はないかもしれませんが,忘れてしまった方も多いかと思います.そこで,ここでは,主要な項目・式の羅列程度の形で記述しておきます.もう少し詳細な説明に関しては,本文,または,「基礎数学」を参照してください.
- 数と式
- 数

- (1) 整数 ・・・, -2, -1, 0, 1, 2, ・・・
- 素数: 1 より大きい整数のうち,1 と自分自身以外の整数では割り切れないような整数 2, 3, 5, 7, 11, 13, ・・・
- 素因数分解: 自然数を素数の積の形で表現すること 60 = 22 × 3 × 5
- 最大公約数: 2 つ以上の正の整数に共通な約数のうち最大のもの 12 ( = 22 × 3 )と 18 ( = 2 × 32 )の最大公約数 = 2 × 3 = 6
- 最小公倍数: 2 つ以上の正の整数に共通な倍数のうち最小のもの 12 ( = 22 × 3 )と 18 ( = 2 × 32 )の最小公倍数 = (2 × 3) × 2 × 3 = 36
- 素数: 1 より大きい整数のうち,1 と自分自身以外の整数では割り切れないような整数 2, 3, 5, 7, 11, 13, ・・・
- (2) 有理数 分数表現可能な数(分数表現は,整数,有限小数,または,循環小数に変換可能)
- 有限小数 1 / 2 = 0.5, 1 / 4 = 0.25, ・・・
- 循環小数 1 / 3 = 0.3333・・・, 1 / 7 = 0.14285714・・・, ・・・
- 有限小数 1 / 2 = 0.5, 1 / 4 = 0.25, ・・・
- (3) 無理数 有理数を除くすべての実数(π, 3 の平方根, ・・・)
- a の平方根: 2 乗すると a ( a ≧ 0 )になる数(有理数または無理数)
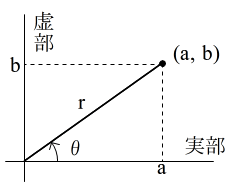
- (4) 複素数 a + bi
- 虚数単位: 2 乗すると -1 になる数
- 複素数と複素平面
- α = a + bi a : 実部,b : 虚部
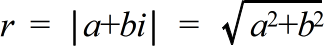
- r: α の絶対値
- θ: α の偏角
- α = r ( cosθ + i sinθ ): α の極形式
- ド・モアブルの定理 複素数 x = r ( cosθ + i sinθ ) に対し,
- xn = rn ( cos nθ + i sin nθ )
- α = a + bi a : 実部,b : 虚部
- 虚数単位: 2 乗すると -1 になる数
- (5) n 進法
- a2a1a0 = a2 × n2 + a1 × n1 + a0 × n0 0 ≦ ai ≦ (n-1)
- 例: 7 進法の 365 → 10 進法?
- (365)7 = 3 × 72 + 6 × 71 + 5 × 70 = (194)10
- 例: 10 進法の 194 → 7 進法?( 10 進法 → n 進法: n で割っていき,その際に生じた余りを下から順に並べる)
- 7)194
- 7) 27 ・・・ 余り 5
- 7) 3 ・・・ 余り 6
- 0 ・・・ 余り 3
- 式
- (1) 整式: 単項式(数や文字の積だけの形で表された式,3ax2,5y,・・・)と多項式(単項式の和や差,3ax2 - 4bx + 5,・・・)
- (2) 因数分解: 1 つの多項式を複数の整式の積で表現すること(各整式を元の多項式の因数と呼ぶ).
- 2x2 + 8xy = 2x(x + 4y)
- x2 ± 2xy + y2 = (x ± y)2
- x2 - y2 = (x + y) (x - y)
- x2 + (a + b)x + ab = (x + a) (x + b)
- acx2 + (ad + bc)x + bd = (ax + b) (cx + d)
- (1) 整式: 単項式(数や文字の積だけの形で表された式,3ax2,5y,・・・)と多項式(単項式の和や差,3ax2 - 4bx + 5,・・・)
- 方程式と不等式
- (1) 等式: 2 つの数量の関係を等号を使って表現したもの
- (2) 方程式: 変数の値によって,等号の左辺と右辺の値が等しくなったり,異なったりするような等式のことであり,等式が成立する変数の値のことを方程式の解,また,その解を求めることを方程式を解くといいます.
- (3) 連立方程式: 複数の等式によって構成される方程式.特に,変数の数が n の場合を n 元連立方程式といいます.
- (4) n 次方程式: 方程式を構成する各項の次数の最大値が n である方程式
- (5) 不等式: 等式における等号を大小関係を表す不等号に置き換えた式であり,方程式を解く場合と同様,大小関係が成立する変数の値(の範囲)を求めることを不等式を解くといいます.
- (6) 2 次方程式の解(根): 2 次方程式 ax2 + bx + c = 0 の解(根)は,判別式,
- D = b2 - 4ac
- の値によって,次のように,重解(重根),実数解(実根),または,虚数解(虚根)のいずれかになります.
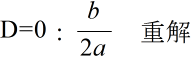
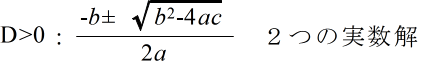
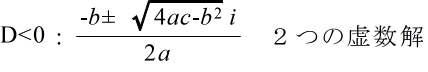
- 2 次方程式 ax2 + bx + c = 0 の2つの解を α,β とすると,2 次方程式の係数間には以下のような関係があります(根と係数の関係).
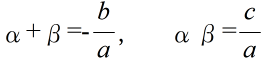
- 逆に,α と β を 2 つの解とする 2 次方程式は,
- (x - α)(x - β) = 0 ∴ x2 - (α + β)x + αβ = 0
- のように表せます.したがって,α + β = p,αβ = q とすると,α と β は,次の 2 次方程式の解となります.
- x2 - px + q = 0
- (1) 等式: 2 つの数量の関係を等号を使って表現したもの
- 恒等式
- 等式に含まれている係数以外の文字に任意の数を代入しても,常に等号が成立する式のこと.例えば,
- ax2 + 3bx + c = 9x + 3
- が,x に関する恒等式であるということは,x がどのような値であっても等号が成立しなければなりません.そのためには,左辺と右辺の各項の係数が等しくなければなりません.つまり,a = 0,3b = 9,c = 3 を満たす必要があります.
- ブール代数と命題論理
- (1) ブール代数
- 1 と 0 だけからなる集合を考え,その集合上で(各変数の取り得る値は 1 又は 0 となる),下の表に示すような 3 つの演算,論理和( OR 演算,+),論理積( AND 演算,・),及び,否定( NOT 演算, )を定義します.このような体系をブール代数と呼びます.
論理和 論理積 否定 X Y X+Y X Y X・Y X X 0 0 0 0 0 0 0 1 0 1 1 0 1 0 1 0 1 0 1 1 0 0 1 1 1 1 1 1 - ブール代数における演算には,以下に示すような性質があります.
- 交換律 X + Y = Y + X
- 分配律
- X ・ (Y + Z) = (X ・ Y) + (X ・ Z)
- X + (Y ・ Z) = (X + Y) ・ (X + Z)
- 単位元の存在 X ・ 1 = X
- 零元の存在 X + 0 = X
- 補元の存在
- X + X = 1
- X ・ X = 0
- 単位元の性質 X + 1 = 1
- 零元の性質 X ・ 0 = 0
- 対合律 X の否定 = X (二重否定律)
- 吸収律
- X + (X ・ Y) = X
- X ・ (X+Y)=X
- ベキ等律
- X + X = X
- X ・ X = X
- 結合律
- X + (Y + Z) = (X + Y) + Z
- X ・ (Y ・ Z) = (X ・ Y) ・ Z
- ド・モルガンの法則
- X + Y = X ・ Y
- X ・ Y = X + Y
- X ・ (Y + Z) = (X ・ Y) + (X ・ Z)
- なお,以下のような関係もよく利用される.
- 含意 X → Y = X + Y
- 同値 X ⇔ Y = (X → Y) ・ (Y → X) = (X + Y) ・ (X + Y)
- (2) 命題論理
- 命題とは,真か偽の値をとり,その両方を同時に値とはし得ないような言明文をいいます.命題論理は,命題 P,Q,・・・ と論理結合子(∨,∧,~)からなる論理体系であり,言葉や記号の違いを除けば,ブール代数と全く同じ構造となります.命題論理では,推論を行うため,含意( P → Q = ~P ∨ Q,「P ならば Q」と読む )という形式がよく使用されますが,含意には以下に示すような性質があります.
- 対偶: ~Q → ~P (Q でないならば P でない)
- 「P → Q」が真であれば常に真となる
- 逆: Q → P (Q ならば P)
- 「P → Q」が真であっても常に真とは限らない
- 裏: ~P → ~Q (P でないならば Q でない)
- 「P → Q」が真であっても常に真とは限らない
- 推論とは,各言明文に明白に述べられていない事実を引き出すことであり,命題論理における代表的推論方法として以下のようなものがあります.
- 肯定式 「P」という事実,及び,「P→Q」という事実から「Q」という事実を推論する
- 否定式 「~Q」という事実,及び,「P→Q」という事実から「~P」という事実を推論する
- 三段論法 「P→Q」という事実,及び,「Q→R」という事実から「P→R」という事実を推論する
- (1) ブール代数
- 数
- 図形
- 直線と角度
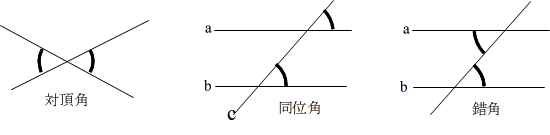
- 三角形と多角形
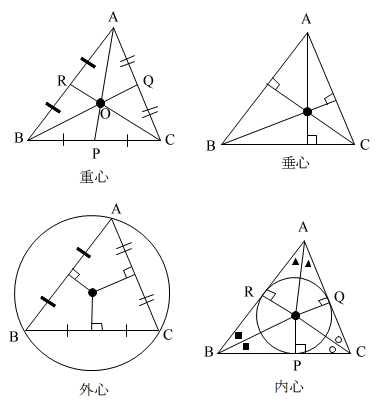
- (1) 重心,垂心,外心,内心
- 重心: 3 つの中線の交点
- AO : OP = 2 : 1
- BO : OQ = 2 : 1
- CO : OR = 2 : 1
- 垂心: 各頂点から対辺に引いた垂線の交点
- 外心: 各辺の垂直二等分線の交点
- (三角形に対する外接円の中心)
- 内心: 各角の二等分線の交点
- (三角形に対する内接円の中心)
- AR = AQ, BP = BR, CQ = CP
- 三角形 ABC の頂角 A の二等分線が対辺 BC と交わる点を D とすると,以下に示すような性質があります.
- BD : DC = AB : AC
- 重心: 3 つの中線の交点
- (2) 内角(赤で示した角)と外角(黒で示した角)
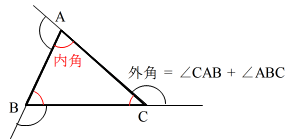
- 内角の和 = 180 × (n - 2) 度 ( n 角形)
- 外角の和 = 360 度
- (3) 面積
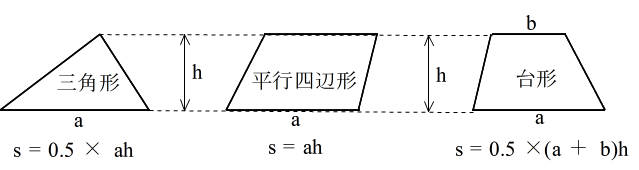
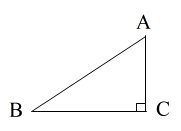
- (4) 三平方の定理(ピタゴラスの定理,右図)
- AB2 = BC2 + CA2
- 円
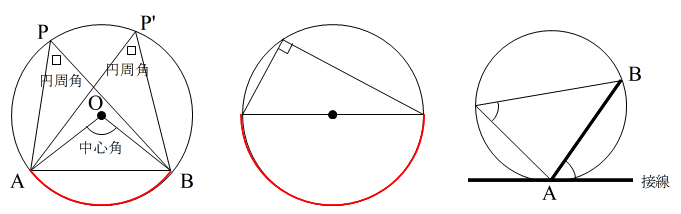
- (1) 円周角と中心角
- 中心角 = 2 × 円周角
- 同じ弧に対する円周角は等しい(上の左図)
- 半円の弧(中心角が 180 度)に対する円周角は 90 度(上の中央図)
- 中心角 = 2 × 円周角
- (2) 円と接線 円の接線とその接点を通る弦(上の右図における弦 AB )の作る角は,その角の内部にある孤に対する円周角に等しい
- (3) 面積 円の半径を r,円周率を π とすると,その面積は,πr2
- 合同と相似
- 合同: 2 つの図形に対し,一方の図形を動かして他方の図形に重ね合わせることができるとき
- 相似: 2 つの図形に対し,一方の図形を一定の割合で縮小又は拡大すると他方の図形と合同になるとき
- 合同: 2 つの図形に対し,一方の図形を動かして他方の図形に重ね合わせることができるとき
- 直線と角度
- 関数とグラフ
- 点と座標
- (1) 直線上の点と座標
- 内分点 AP : PB = m : n
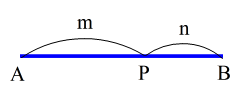
- 外分点 AP : PB = m : n

- 内分点 AP : PB = m : n
- (2) 平面上の点と座標
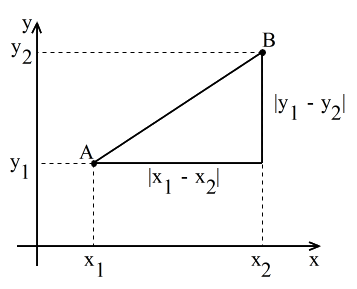
- 2 点間の距離
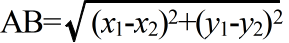
- 内分点と外分点
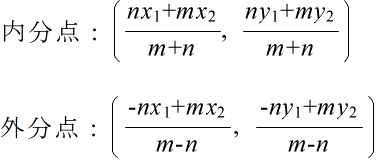
- (1) 直線上の点と座標
- 比例と反比例
- (1) y は x に比例( a:比例定数) y = ax → 傾きが a の直線
- (2) y は x に反比例( a:比例定数) y = x / a ( xy = a ) → 双曲線
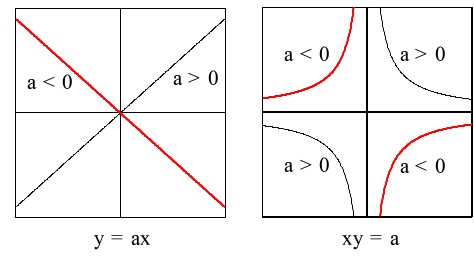
- (1) y は x に比例( a:比例定数) y = ax → 傾きが a の直線
- 1 次関数と 2 次関数
- (1) 1 次関数
- 直線の方程式
- ax + by + c = 0
- y = kx + m b ≠ 0 である場合
- k:傾き, m:y 切片
- 2 直線の関係 2 直線 y = k1x + m1 と y = k2x + m2 の間には,以下に示すような関係が成立します.
- k1 = k2 → 2直線が平行
- k1k2 = -1 → 2直線が垂直(直交)
- 点 Q(x0, y0) から,直線 ax + by + c = 0 までの距離(点 Q から直線におろした垂線の長さ)
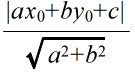
- 直線の方程式
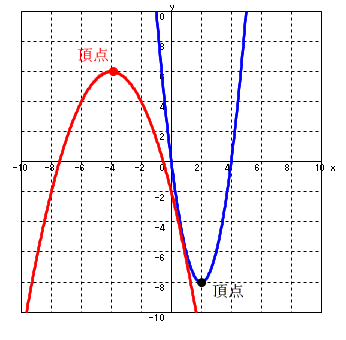
- (2) 2 次関数(放物線)
- 放物線の方程式
- y = ax2 + bx + c = a (x - p)2 + q
- 例:
- y = 2 (x - 2)2 - 8 (青色)
- 頂点: (2, -8), 軸: x = 2
- y = -0.5 (x + 4)2 + 6 (赤色)
- 頂点: (-4, 6), 軸: x = -4
- 放物線の極大値と極小値
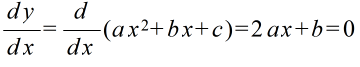
- を満たす点(微分係数が 0 となる点),つまり,頂点で極小( a > 0 ),または,極大( a < 0 )になる.
- 放物線の方程式
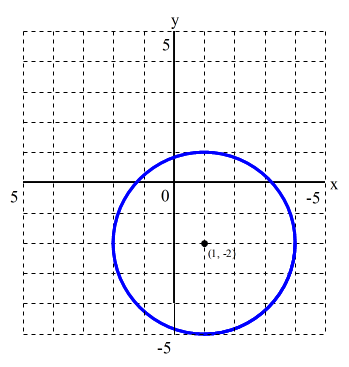
- (3) 2 次関数(円)
- 中心が (a, b),半径が r の円の方程式は,
- (x - a)2 + (y - b)2 = r2
- 例: 中心が (1, -2),半径が 3 の円の方程式
- (x - 1)2 + (y + 2)2 = 9
- (1) 1 次関数
- 関数と方程式
- (1) 1 次関数と 1 次方程式
- 1 次方程式,
- ax + b = 0
- の解は,1 次関数,
- y = ax + b
- の x 軸との交点の x 座標に相当します.
- (2) 2 次関数と 2 次方程式
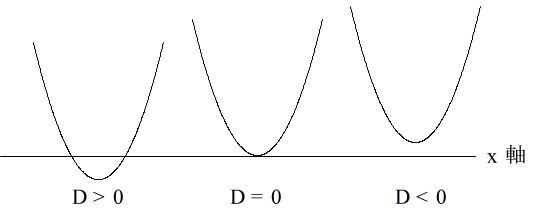
- 2 次方程式 ax2 + bx + c = 0 の解は,放物線 y = ax2 + bx + c と 直線 y = 0 ( x 軸)との交点の x 座標の値になります.判別式 D = b2 - 4ac の値が正,0,又は,負であることは,下の図( a > 0 の場合)に示すように,放物線が x 軸と交わる,接する,又は,交わらないということに相当します.
- (1) 1 次関数と 1 次方程式
- 三角関数
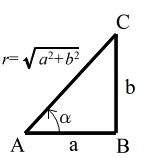
- (1) 三角比
- 三角比
- 右図に示すような直角三角形 ABC において,三角形の大きさによらず,角 α の大きさだけによって決まる正弦( sine ),余弦( cosine ),及び,正接( tangent )を以下のように定義し,これらを三角比と呼びます.
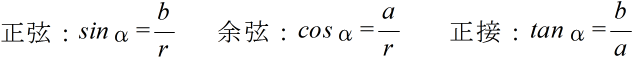
- 余弦定理と正弦定理
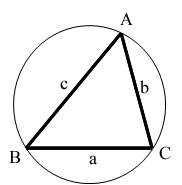
- 余弦定理
- a2 = b2 + c2 - 2bc cos A
- b2 = c2 + a2 - 2ca cos B
- c2 = a2 + b2 - 2ab cos C
- 正弦定理( R: 三角形の外接円の半径)
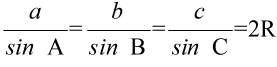
- 弧度法 円弧の長さ l(エル) と扇型の半径 r の比( l / r )をとると,円の大きさにかかわらず,同じ角度 θ に対してこの比は一定となります.そこで,この比(ラジアン)によって角度の大きさを表す方法を弧度法と呼びます.
- x 度 → ( 2πx / 360 ) ラジアン
- 三角比
- (2) 三角関数 角度とその角度における三角比の関係を式として表現したもの
- 加法定理
- sin(α + β) = sinα cosβ + cosα sinβ
- sin(α - β) = sinα cosβ - cosα sinβ
- cos(α + β) = cosα cosβ - sinα sinβ
- cos(α - β) = cosα cosβ + sinα sinβ
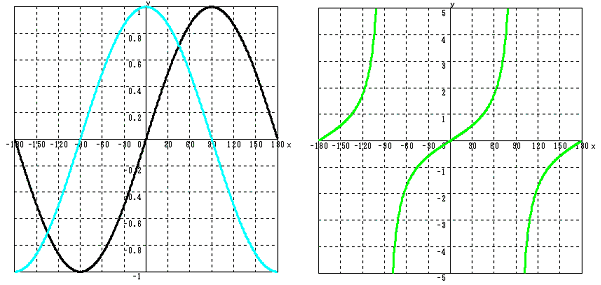
- 三角関数のグラフ
- y = sin (x) (左のグラフの黒色)
- y = cos (x) (左のグラフの空色)
- y = tan (x) (右のグラフ)
- 加法定理
- (1) 三角比
- 指数関数と対数関数
- (1) 指数関数
- a を 底とする指数関数
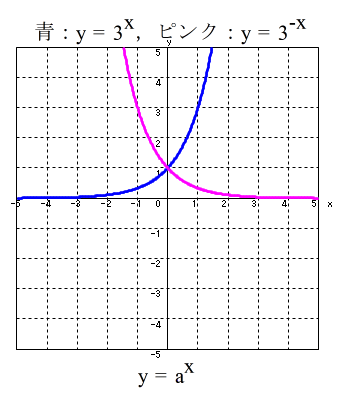
- (2) 対数関数
- a を底とする対数関数
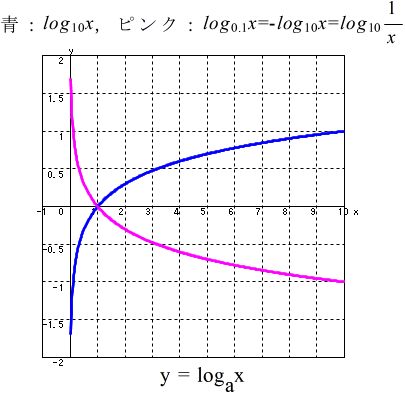
- (1) 指数関数
- 点と座標
- 数列
- 等差数列
- (1) 一般項 an
- an = a1 + (n - 1) d ( a1: 初項,d: 公差)
- (2) 初項から第 n 項までの和
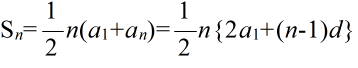
- (1) 一般項 an
- 等比数列
- (1) 一般項 an
- an = a1r(n - 1) ( a1: 初項,r: 公比)
- (2) 初項から第 n 項までの和
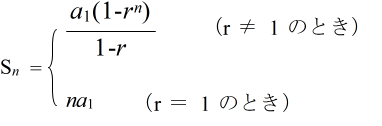
- (1) 一般項 an
- 等差数列
- 順列・組合せ
- 集合
- 集合
- ある定まった範囲にある対象をひとまとめにしたものを集合( set )といい,集合を構成する一つ一つの対象を集合の要素あるいは元といいます.一般に,x が集合 A の要素であるとき,
- x ∈ A
- と表し,逆に,A の要素でないときは,
- x ∈/ A
- と表します.
- 集合 X に含まれるすべての要素 x が,集合 Y に含まれるならば,また,そのときに限って,集合 X は,集合 Y に含まれる(集合 X は,集合 Y の部分集合である)といいます.このことを形式的に記述すると,以下のようになります.
- X ⊂ Y ⇔ ∀x ∈ X ならば x ∈ Y
- ここで,記号「∀」は,「すべての」と読み,「∀x ∈ X」によって,「集合 X に含まれるすべての要素」を意味します.
- 2 つの集合 X,Y について,そのどちらかに含まれる要素からなる集合を X と Y の和集合といい,
- X ∪ Y (= {x | x ∈ X,または,x ∈ Y})
- と表します.X と Y の両方に含まれる要素からなる集合を X と Y の共通集合(積集合)といい,
- X ∩ Y (= {x | x ∈ X,かつ,x ∈ Y})
- と表します.また,X の部分集合 E について,X の要素で E に含まれない要素の集合を E の補集合といい,Ec で表します.上で述べた関係をベン図で表現すると,以下のようになります.
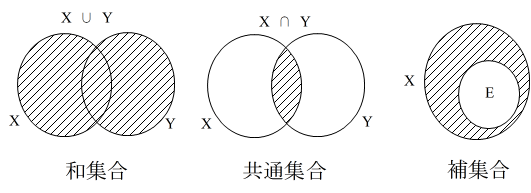
- 形式的に,全体集合(対象としているすべての要素を含む集合) X と空集合(一つも要素を含まない集合) φ について
- Xc = φ
- φc = X
- とします.
- 集合の諸性質
- 以下に述べる集合の諸性質において,
- X : 全体集合
- E, F, G : X の任意の部分集合
- とします.
- 可換律
- E ∪ F = F ∪ E
- E ∩ F = F ∩ E
- 結合律
- E ∪ ( F ∪ G ) = ( E ∪ F ) ∪ G
- E ∩ ( F ∩ G ) = ( E ∩ F ) ∩ G
- 分配律
- E ∪ ( F ∩ G ) = ( E ∪ F ) ∩ ( E ∪ G )
- E ∩ ( F ∪ G ) = ( E ∩ F ) ∪ ( E ∩ G )
- 二重否定律
- ( Ec )c = E
- 排中律
- E ∪ Ec = X
- 矛盾律
- E ∩ Ec = φ
- ド・モルガン律
- ( E ∪ F )c = Ec ∩ Fc
- ( S ∩ F )c = Ec ∪ Fc
- 集合
- 線形代数
- 我々は,数値を使用した演算(加減乗除)をしばしば行います.場合によっては,数値だけでなく,変数を使用した式(方程式)を定義し,その変数の値を求めたいような場合もあります.これらことを一般的・抽象的に記述し,方程式の解を求めたり,式や計算そのもの性質を探求しようとする数学が線形代数です.なお,線形代数においては,変数に関して,その 1 次式だけを対象とします(線形性).計算の基盤となる部分であり,様々な分野で必要とされます.特に,ベクトルや行列に対する概念は重要です.
- ベクトル( vector )
- 例えば,温度や長さなどは,単位は別として,その大きさだけで表現できます.しかし,力のように,大きさだけでなく,力が加えられる向きも重要になる場合があります.また,CG ( Computer Graphics )における線分においても,その長さだけではなく方向も重要になります.そのような場合に使用されるのがベクトルです.それに対応して,大きさだけを持った量をスカラーと呼びます.
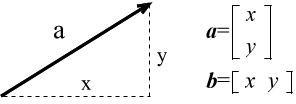
- ベクトルは,一般に,a,b,・・・ のように,英小文字の太字で表現されます.上図に示すのは,平面上のベクトル( 2 次元ベクトル)の例です(矢印の長さがベクトルの大きさ),2 次元ベクトルは,2 つの要素を持っており(右の例では,x と y ),通常,縦長の形(列ベクトル)で表しますが,横長の形で表す場合もあります( b,行ベクトル).
- ベクトルどうしの加算,減算は,要素どうしの加算,減算として定義できます.また,ベクトルにスカラーを乗じると,すべての成分をスカラー倍したベクトルになります.同じ次元のベクトルどうしの乗算には,内積( a・b )と外積( a×b,一般に,a×b≠b×a )という 2 種類の方法が存在します.特に,内積は,2 つのベクトル a,b が直交するときに 0 となるため,よく利用されます.
- 行列( matrix )
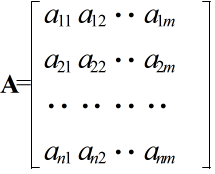
- 数値を上図に示すように,n 行 m 列の形に並べたものを,n 行 m 列行列( n×m 型行列)といいます.行列は,一般に,A,B,・・・ のように,英大文字の太字で表現されます.この定義から,先に述べたベクトルは,n 行 1 列行列(行ベクトルの場合は,1 行 n 列行列)とみなすこともできます.
- 2 つの行列が同じ n 行 m 列行列であれば,ベクトルと同様,行列どうしの加算,減算を,要素どうしの加算,減算として定義できます.また,行列のスカラー倍も,ベクトルと同様,すべての成分をスカラー倍した行列として定義されます. 行列 A が n 行 m 列行列,行列 B が m 行 l(エル) 列行列の場合に限り,行列 A と行列 B の積 AB が定義でき,結果は,n 行 l 列行列になります.なお,積の条件を満たしたとしても,一般に,AB と BA は等しくなりません.
- 行列は,様々な分野で使用されますが,ここでは,連立一次方程式を取り上げてみます.例えば,
2x + y + z = 7 x + y - z = 2 3x + 2y - 2z = 5
- のような連立一次方程式は,3 つの行列,
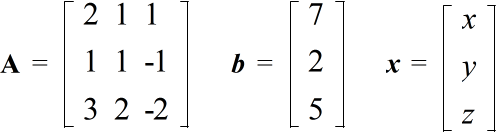
- を導入すると,
Ax = b
- のように,非常に簡単に記述できます.記述方法が簡単になることも,行列を使用する大きな利点です.この方程式の解も,逆行列 A-1(後述)を利用して,以下のように簡単に記述できます.
x = A-1b
- また,ベクトルに行列を乗ずる演算は,ベクトルの拡大・縮小,座標軸の回転等に対応します.この性質は,アフィン変換という形で,CG ( Computer Graphics )の分野で多く利用されています.アフィン変換は,線型変換(回転,拡大・縮小,剪断)と平行移動の組み合わせであり,一般的に,
- Ax + t
- の形で記述できます.ここで,t は平行移動量を表すベクトルです.2 次元ベクトルに対するアフィン変換は,下に示すように,次元を 1 つ上げた 3 次元の行列及びベクトルで表します.この行列の左上の 2 行 2 列が行列 A を,3 列目の上 2 つの要素がベクトル t に対応します.
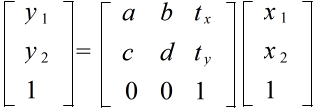
- 行列式
- n×n ( n 次)の正方行列 A に対して,以下のような形で示される多項式を,行列 A の行列式といいます.行列 A の要素がすべて定数の場合は,行列式の値も定数になります.なお,正方行列とは,行と列の数が等しい行列のことです.
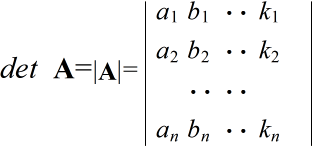
- 逆行列
- 行列 A が n×n の正方行列であり,AX = XA = I となるような正方行列 X が存在するとき,X を A の逆行列といい,A-1 で表します.逆行列が存在するための必要十分条件は,行列 A の行列式の値が 0 とならないことです( |A| ≠ 0 ).このとき,正方行列 A は正則であるといい,A を正則行列といいます.なお,I ( E とも表す)は単位行列と呼ばれ,対角成分がすべて 1,他の成分はすべて 0 であるような行列です( aii = 1,aij = 0,i ≠ j ).
- 固有値と固有ベクトル
- 一般に,0 でない n 次元ベクトル x に,n 次の正方行列 A を乗じると,ベクトルの大きさや方向が変化します.しかし,
- Ax = λx(λ:スカラー)
- という関係が成立する場合があります(大きさだけが λ 倍される).このとき,λ を行列 A の固有値,x を固有ベクトルと呼びます.この定義より,固有値 λ は,
- |A - λI| = 0 ( n 次代数方程式: 固有方程式,又は,特性方程式という)
- の根となります.一般に,固有ベクトルは一意には決まりません.固有ベクトルをスカラー倍したものも固有ベクトルになります.なお,固有値や固有ベクトルは,後に述べる微分方程式や多変量解析において重要な役割を果たします.
- 微分積分
- 微分や積分は様々な分野で利用され,非常に重要な概念です.難しい概念のように思われがちですが,決してそうではありません.以下に述べるように,微分・積分は,我々の日々の生活の中でほとんど意識することなく利用しているような簡単な概念です.また,利用することなしでは生きていくことすら困難になるといっても過言ではありません.
- 例えば,山へ登っている途中で道に迷った場合について考えてみます.また,霧のため,周りはほとんど見えないものとします.尾根へたどり着けば道が存在すると思われるので,その方向(高い方)へ登っていきたいとします.このとき,どのような方向に向かえばよいでしょうか.周りがほとんど見えなくても,足下近傍の情報から,どちらの方向へ向かえば高い方へ向かうかの見当が付きます.このとき使用している情報 ”傾斜”は,正に,位置を微分するという動作から得られたものです.
- 今,A という場所から B という目的地に向かって歩いていたとします.A から B までの距離は分かっており,1 時間程度で行ける場所だとします.30 分程度歩いたとき,「これで半分来たか.あと,30 分程度で着くだろう」といったようなことを考えるはずです.このような推論が可能であるためには,歩く速度-位置を微分したもの-を知っている必要があります.また,30 分歩いた時の移動距離-速度を 30 分間積分したもの-も知っている必要があります.
- 以上の例で述べたように,微分は変化率に基づいた予測のために,また,積分は過去の行動を積み重ねた結果を表す(和の拡張)ために使用されます.我々は,微分や積分を,何の困難さもなく普段使用しているはずです.ここでは,これらの概念について,もう少し精密に検討していきます.
- 微分
- 定義
- 関数 y = f(x) が与えられたとき,関数上の点 A(a, f(a)) において,

- などによって表される値を f(x) の x = a における微分係数といいます.微分係数は,x = a の近傍において,x を変化させたとき,y がどの程度変化するかを示す値( y の変化量 / x の変化量)であり,x = a における関数 f(x) の接線の傾きに相当します.接線の傾きは,変数 x が変化したとき,変数 y がどのように変化するかを予測するために使用できます.関数が極大や極小になる点(山の頂上など)では,微分係数の値が 0 になることから,関数の極大値や極小値を求めたいような場合にも利用されます.
- 上の a は任意の数ですから,変数 x と考えると,
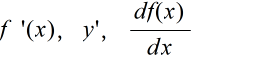
- のような記述が可能です.この f’(x) などを f(x) の導関数といい,導関数 f'(x) を求めることを,f(x) を( x で)微分するといいます.微分した関数をさらに微分することも可能です.導関数の導関数は 2 階の(または,2 次の)導関数とよび,一般に,n 階の(または n 次の)導関数を
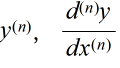
- と表します.
- 多変数の関数に対しては,その中の特定の変数に対する微分も定義できます.例えば,2 変数関数 f(x, y) に対して,y を定数とみなし x で微分したものを x に関する偏導関数といい,以下のように表します.
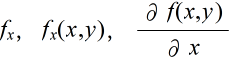
- 同様に,y に関する偏導関数や,2 階以上の偏導関数も定義可能です.
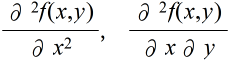
- 公式
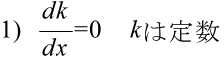
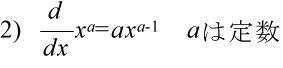


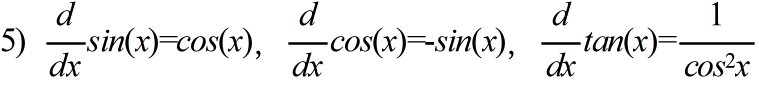
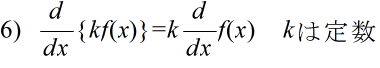
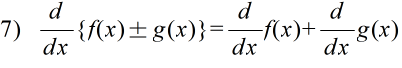
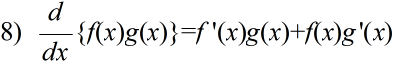
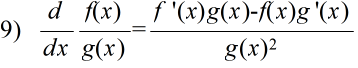
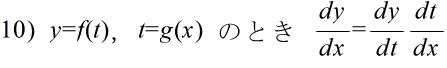
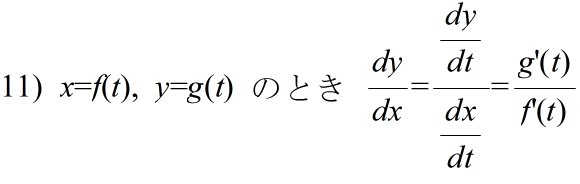
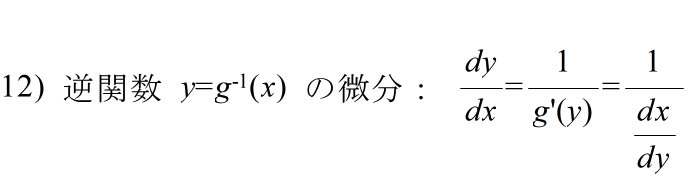
- 定義
- 積分
- 定義
- 関数 f(x) に対して,F'(x) = f(x) となる関数 F(x) を f(x) の原始関数または不定積分といいます.f(x) の不定積分を
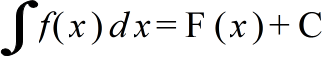
- と表し,これを求めることを f(x) を積分するといいます.C は,任意の定数ですので,その微分は 0 となり,F'(x) = f(x) を満たします.この定数 C を,積分定数といいます.
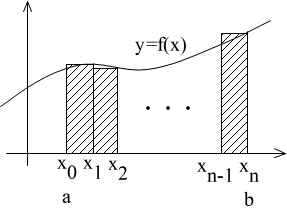
- 閉区間 a ≦ x ≦ b で定義されている関数 f(x) を考えます.閉区間 a ≦ x ≦ b を n 等分して,その分点を,
- a = x0, x1, x2, ・・・, xn = b
- とし,上図のよう矩形(斜線部)を考えます.分割数をより多くしていけば,矩形の面積の和は,x = a,x = b,y = 0,及び,関数 y = f(x) で囲まれた部分の面積に近づいていきます.この極限を,f(x) の a から b までの定積分といい,以下のように表します.
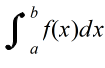
- 不定積分の公式(積分定数は省略)
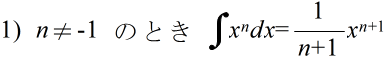
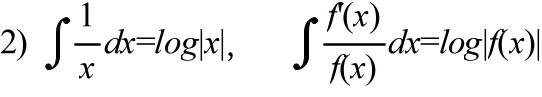
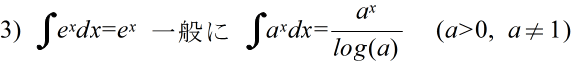
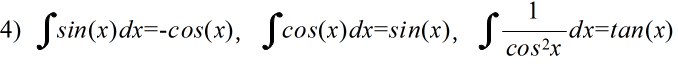
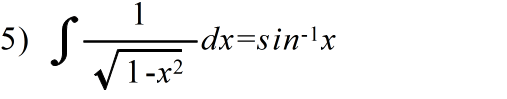
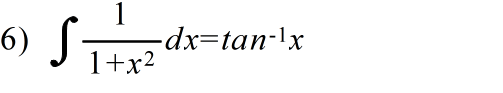
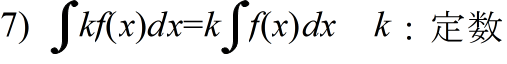
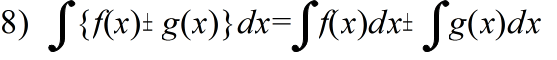
- 定積分の公式
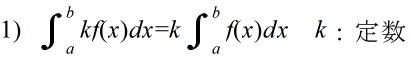
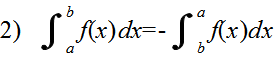
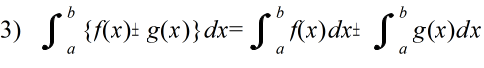
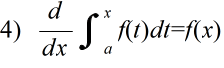
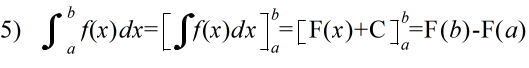
- 置換積分法 x = φ(t)
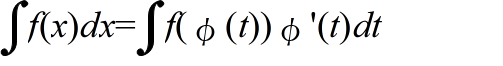
- 部分積分法 G(x):g(x) の原始関数
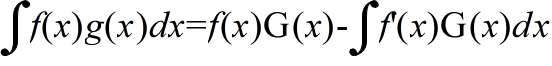
- 定義
- 確率と統計
- 例えば,「 100 ㎞/h で走っている列車の 10 分後の位置」,「 100 m の高さから落とした石が地面に落下する時間」などは,様々な要因によって多少の誤差は生じますが,何らかの式を用いて計算可能です.しかし,「サイコロを投げたとき出る目」のように,計算不可能な現象が多く存在します.確率統計は,そのような現象を扱う数学です.
- 確率
- 一定の条件の下で繰り返し行うことができ,その結果が偶然に支配されるような実験や観測を一般に試行(サイコロを投げるなど)といいます.試行によって起こる可能性のあるすべての事柄の集合 Ω が確定しているとき,その集合を考えている試行の標本空間といい,その要素を標本点,または,単に標本空間の点といいます.
- 標本空間 Ω の部分集合を事象といい,試行の結果が 1 つの事象 A (サイコロを投げ,偶数の目が出ることなど)に属するとき,事象 A が起こったといいます.標本点の 1 つ 1 つを特に根元事象( 1 の目が出ることなど)といいます.それに対して,2 個以上の点からなる事象を複合事象といいます.また,標本空間全体を全事象,決して起こらない事柄は空集合 φ で表され,それを空事象といいます.
- 標本空間 Ω の各事象 A に対して次の 3 つの条件を満たす実数 P(A) が対応させられるとき,その値 P(A) を事象 A の起こる確率といいます.各事象に対して確率が与えられる標本空間を確率空間といい,各事象を確率事象といいます.
- (1) 任意の事象 A に対して,0 ≦ P(A) ≦ 1
- (2) P(Ω) = 1, P(φ) = 0
- (3) 事象 A と B が互いに排反,即ち A ∩ B = φ ならば,以下の関係が成立する.
- P(A ∪ B) = P(A) + P(B)
- 確率変数
- 標本空間 Ω で,ある属性について標本がとる可能性がある異なる数値が
- x1,x2,・・・,xk
- であるとします.各標本に対してそれのとる値を対応させる変数 X を考えます.Ω 上で X がそれぞれの値をとる確率が定まっているとき,X を確率変数(random variable,stochastic variable)(離散型確率変数)といい,x1,x2,・・・,xk を X の標識といいます.
- 確率変数 X が値 xi をとるという事象を
- { X = xi }
- で表し,その確率を
- P(X = xi) = pi (i = 1, 2, ・・・, k)
- で表します.このように,X がとる値それぞれに対して確率が定まるため,確率は関数の形で,
- f(x) = pi ( x = xi のとき)
- = 0 (その他の x )
- のように記述できます.この関数を確率変数 X の確率密度関数(probability density function)といい(離散的な場合は,単に,確率関数ということもある),確率変数 X は,確率分布 f(x) に従うといいます.
- 確率変数 X がある値 x に対して,X ≦ x である確率 P(X ≦ x ) を,確率変数 X の確率分布関数(distribution function),または,累積分布関数(cumulative distribution function)といいます.これを F(x) とすれば,次のようにかけます.
- F(x) = P(X ≦ x)
- 確率変数が連続値を取るような分布も存在します.次の式で表される f(x) が存在するとき,f(x) を確率変数 X の確率密度関数といいます.
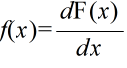
- また,確率分布関数 F(x) は f(x) から
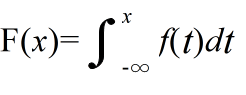
- として与えられます.
- 平均と分散
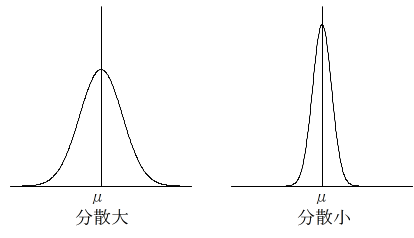
- 平均(集合平均,期待値)
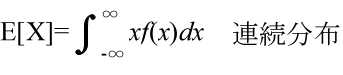
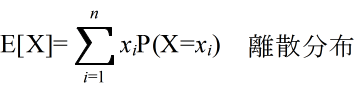
- 分散( σ2 )と標準偏差( σ )
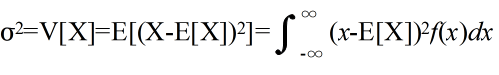
- 分散(標準偏差)は,データのバラツキ具合を表します.分散が大きいほど,バラツキの度合いが大きくなります.例えば,試験を行った結果,ほとんどの人が平均点前後であった場合は,分散が小さくなります.逆に,0 点から 100 点まで,大きくばらついた場合は分散が大きくなります.
- 平均(集合平均,期待値)
- 確率分布
- 二項分布(離散型分布)
二項分布の確率密度関数
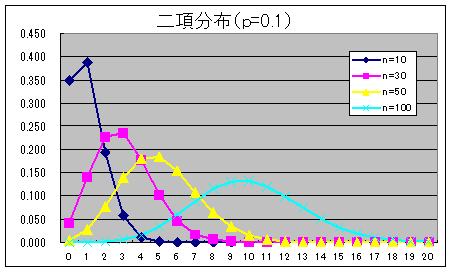
- 繰り返し行われる独立試行で,もし各々の試みに対して単に 2 つの結果だけが可能で,それらが起こる確率が各試行を通じて一定である場合,その試行をベルヌーイ試行といいます.成功の確率が p で失敗の確率が q = 1 - p であるベルヌーイ試行を n 回行った結果,x 回成功する確率(確率密度関数)は以下のようになり,この分布を母数 p の二項分布と呼びます.
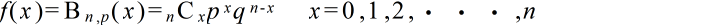
- なお,二項分布の平均,及び,分散は以下のようになります.
- 平均: E[X] = np, 分散: V[X] = npq
- ポアソン分布(離散型分布)
ポアソン分布の確率密度関数
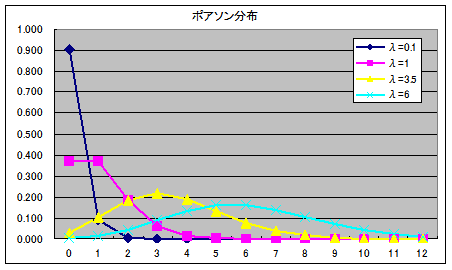
- 二項分布は,p の値が小さく,n の値が非常に大きくなると,λ = np のポアソン分布に近づきます.単位時間内に到着する電話の呼び数 x の分布等がポアソン分布に従うことが良く知られています.母数 λ のポアソン分布の確率密度関数,平均,及び,分散は以下のようになります.
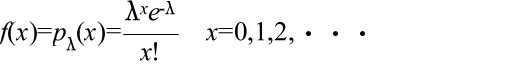
- 平均: E[X] = λ, 分散: V[X] = λ
- 一様分布(連続型分布)
- 一様分布の確率密度関数,平均,及び,分散は以下のようになります.
- 密度関数 f(x) = 1 / (b - a) a ≦ x ≦ b
- = 0 x < a,または,x > b
- 平均: E[X] = (a + b) / 2, 分散: V[X] = (a - b)2 / 12
- 指数分布(連続型分布)
指数分布の確率密度関数

- 指数分布は,ポアソン分布と強い関係があります.例えば,電話の呼び間隔が平均 1 / λ の指数分布をするとき,単位時間内に到着する電話の呼び数の分布は平均 λ のポアソン分布をします.母数 λ の指数分布の確率分布関数,確率密度関数,平均,及び,分散は以下のようになります.
- 分布関数 F(x) = 1 - e-λx x ≧ 0
- = 0 x < 0
- 密度関数 f(x) = λe-λx x ≧ 0
- = 0 x < 0
- 平均: E[X] = 1 / λ, 分散: V[X] = 1 / λ2
- 正規分布(ガウス分布)(連続型分布) N(μ, σ2)
正規分布の確率密度関数
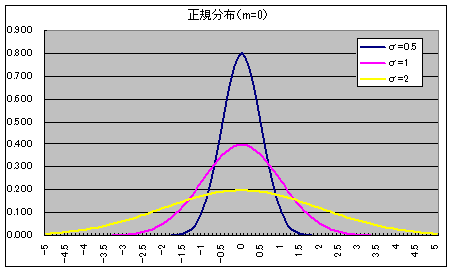
- 正規分布は,非常によく使われる分布です.母数 μ(平均),σ(標準偏差) の正規分布 N(μ, σ2) の確率密度関数は以下のようになります.
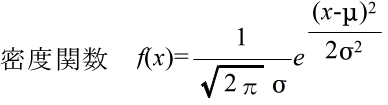
- 平均が 0,標準偏差が 1 である正規分布 N(0, 12) を標準正規分布と呼びます.確率変数 X の分布が N(μ, σ2) の正規分布に従うとき,次の変数変換(標準化変換)によって得られる確率変数 Z は標準正規分布 N(0, 12) に従います.
- Z = (X - μ) / σ
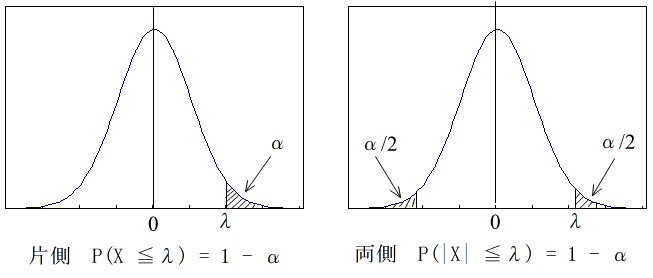
- また,値 α( 0 ≦ α ≦ 1,斜線部の面積)に対して,以下の図に示すような値 λ を正規分布の α 値,または,p %値( p = α×100 )といいます.αは,図からも明らかなように,確率変数の値が λ 以上になる確率(両側の場合は,確率変数の値が λ 以上,又は,ーλ以下になる確率)に相当します.α 値は,後に述べる推定において非常に重要となりますので十分理解しておいてください.なお,正規分布以外の分布に対しても,同様に,α 値を定義することができます.
- 自由度 n の χ2 分布(連続型分布)
自由度 n の χ2 分布の確率密度関数
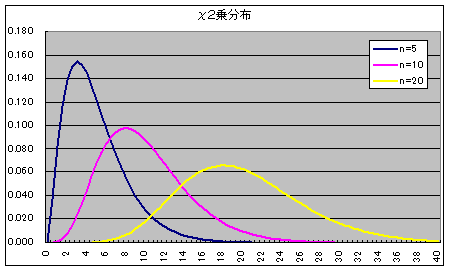
- 自由度 n の χ2 分布の確率密度関数,平均,及び,分散は以下のようになります.
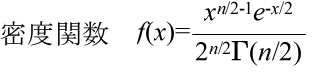
- 平均: E[X] = n, 分散: V[X] = 2n
- ここで,Γ は,ガンマ関数であり,次のように定義されます.
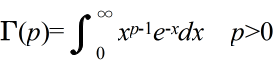
- Γ(1) = 1, Γ(p+1) = pΓ(p)
- Γ(n+1) = n! n: 整数
- 自由度 n の t 分布(連続型分布)
自由度 n の t 分布の確率密度関数
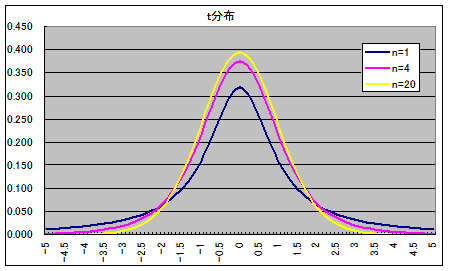
- 自由度 n の t 分布の確率密度関数,平均,及び,分散は以下のようになります.
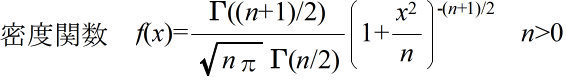
- 平均: E[X] = 0, 分散: V[X] = n / (n - 2) 平均,分散は,n ≧ 3
- 自由度 n1,n2 の F 分布(連続型分布)
自由度 n1,n2 の F 分布の確率密度関数
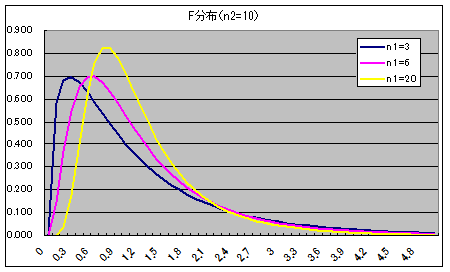
- 自由度 (n1, n2) の F 分布の確率密度関数,平均,及び,分散は以下のようになります.ただし,平均に対しては n2 > 2,分散に対しては n2 > 4 とします.
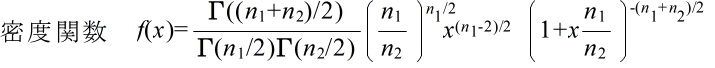

- 二項分布(離散型分布)
- 統計的推定
- 調査や観測の対象となる属性を持つすべての個体の集合を母集団といいます.母集団から取り出された一部のデータの集合を標本といい,データの数を標本の大きさといいます.また,母集団の平均,分散などを母平均,母分散といい,一般に母集団の特性値を母数といいます.
- 母集団からランダムに標本を取り出すことを無作為抽出(random sampling)といい,無作為抽出によって取り出された標本を無作為標本(任意標本)といいます.
- 調査や観測等によって,我々が知りたいのは母集団の特性値-母数-です.観測された標本 x1, x2, ・・・, xn から,母数を推定する方法を統計的推定と呼びます.母平均や母分散を推定する方法として,以下に示すような標本統計量(標本平均,標本分散などは,母平均,母分散等に対する点推定値)がよく使用されます.
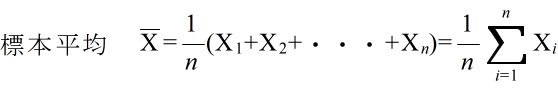
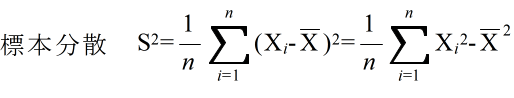

- 標本統計量も一つの確率変数です.従って,その統計量を計算できます.例えば,標本平均と標本分散の平均は以下のようになります.
- E[X] = μ μ:母平均
- E[S2] = (n - 1) σ2 / n σ2: 母分散
- 上式から明らかなように,標本平均の平均は母平均と一致しますが,標本分散に関しては,一致しません.標本平均のように,ある母数 θ が Θ(X1, X2, ・・・, Xn) として推定されるとき,
- E[Θ] = θ
- を満たす,つまり,推定量の平均が母数に一致するとき,推定量 Θ を不偏推定量と呼びます.母分散の不偏推定量は,以下のようになり,先に述べた標本分散の代わりによく使用されます.
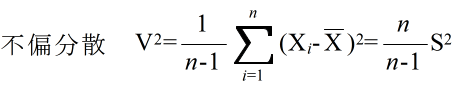
- ただし,不偏分散の平方根は,母標準偏差の不偏推定量にはならないことに注意して下さい.また,多変数の場合は,以下に示すような標本統計量がしばしば使用されます.
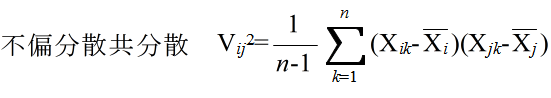
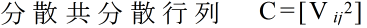
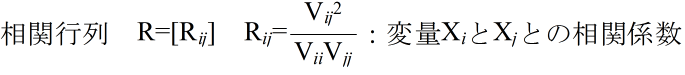
- ただし,
- X1, X2, ・・・, Xm : 確率変数
- Xi1, Xi2, ・・・, Xin : 確率変数 Xi に対する標本確率変数
- とします.
- 統計的検定
- 実験等によって得られた標本統計量に基づき,何らかの推論を行いたい場合があります.例えば,標本平均からその「母平均が μ である」ことを検証したい,2 つの母集団から得られた標本平均に基づき,それらの「母平均が等しい」ことを検証したい,といった場合です.このような場合,まず,一つの仮説 H0(帰無仮説)をたてます.例えば,上の例では,「母平均が μ である」,「母平均が等しい」などがその仮説に相当します.また,上の仮説に対立する仮説,「母平均は μ でない」,「母平均が異なる」などの仮説 H1 を対立仮説といいます.
- 既に述べたように,標本統計量も一つの確率変数です.同じ母集団から採った標本平均であっても,常に同じ値になるわけではありません.したがって,2 つの母集団から得られた標本平均が同じ値になったとしても,必ずしも 2 つの母集団の母平均が等しいことを意味しているわけではありません.同様に,2 つの標本平均が異なっていても,それらの母平均が異なっているとは限りません.
- そこで,以下に述べるような方法によって仮説の正誤を判定します.まず,指定された標本統計量(検定方法毎に異なる)を計算します.標本統計量は設定した仮説の下で何らかの分布をします.得られた標本統計量がその分布の滅多に起こらないような値であったとします.例えば,標本統計量が平均 50,標準偏差 10 の正規分布をしていたとき,実際に得られた標本統計量が 85 であったような場合です.実際,このようなことが起こる確率は,0.001 以下です.このような場合に対する解釈として 2 つあります.一つは,滅多に起こらないことが起こったという解釈です.他の一つは,設定した仮説が間違っていたという解釈であり,一般には,この解釈を採用します.その際,正規分布に対する説明の際に述べた α 値((p×100) パーセント値) λ を使用します.得られた統計量の値が λ より大きい(または,小さい)とき,つまり,統計量に対する分布の基で,得られた統計量の値が実現する確率が α 以下であるとき,最初の仮説が誤っているものとして棄却します.この方法を仮説検定といいます.
- α 値((α×100) パーセント値)として,普通,5 %,または,1 %が用いられ,これを有意水準といいます.仮説 H が有意水準 α で棄却されたとき,検定結果は水準 α で有意差があるといいます.また,仮説を棄却する範囲のことを棄却域といい,確率分布の片側または両側に棄却域をとる場合を,それぞれ片側検定,または,両側検定といいます.
- ある仮説が棄却されたとしても,仮説が誤っていることを意味しているわけではありません.あくまで,得られたデータのもとでは,誤っている可能性が高いことを示唆しているにすぎません.仮説 H0 が正しいにもかかわらず棄却される誤り(第 1 種の誤り)も当然発生します.同様に,棄却されなかったとしても,仮説が正しいことを意味しているわけではないことに,十分注意してください.仮説 H0 が誤っているにもかかわらず採用されてしまう誤り(第 2 種の誤り)が起こる可能性があるからです.
- 例えば,「 100 ㎞/h で走っている列車の 10 分後の位置」,「 100 m の高さから落とした石が地面に落下する時間」などは,様々な要因によって多少の誤差は生じますが,何らかの式を用いて計算可能です.しかし,「サイコロを投げたとき出る目」のように,計算不可能な現象が多く存在します.確率統計は,そのような現象を扱う数学です.
- コンピュータは,「連立 1 次方程式を解く」,「非線形方程式の解を求める」,「積分を行う」など,数学における様々な計算を高速かつ正確に行ってくれます.ここでは,コンピュータによって実行可能な様々な計算及びその方法について簡単に説明します.
- 連立 1 次方程式と逆行列
- 変数の数が少なければ,我々でも,連立 1 次方程式を簡単に解くことができますが,変数が数が多くなれば,ほとんど不可能になります.我々が,2 元や 3 元の連立 1 次方程式を解く場合,「ある式を何倍かして他の式から引く」などの操作によって,変数の数を減らしていきます.コンピュータによるガウス-ジョルダンの消去法も似たような考え方で連立 1 次方程式の解を求めます.また,同じ方法によって,逆行列を計算することも可能です.
- 非線形方程式
- 特別な場合を除き,変数の 5 次以上の項,三角関数,指数関数,対数関数などを含む非線形方程式の解を,手計算によって求めることは困難です.コンピュータに頼ることになります.しかし,残念ながら,コンピュータに非線形方程式を与え,非線形方程式のすべての解(一般的に,非線形方程式の解は複数存在する)を自動的に求めるような方法は存在しません.
- 非線形方程式を解く方法には,大きく分けて,2 種類の方法があります.一つは,関数の微分を利用する方法です.適切な初期値を与え,その点における微分係数を計算し,微分係数から解の位置を予測する(この予測された値が次のステップの初期値となる),といった手順を繰り返す方法です.Newton 法(ニュートン法)では,この方法によって解を求めます.異なる解を求めるためには,異なる初期値を設定する必要があります.初期値が適切であれば,素早く解に収束しますが,そうでなければ,発散して解を求めることができない場合もあります.
- あと一つの方法は,微分を使用しない方法です.その区間内に必ず一つの解が存在する区間 [a, b] を与えます.その後,適切な判断基準によって,区間を徐々に狭くし,解に収束させる方法です.必ず解を求めることができますが,一般に,収束するのに時間がかかります.二分法,セカント法などが,これに相当します.
- 代数方程式と行列の固有値・固有ベクトル
- 上で非線形方程式に対する解の求め方について述べましたが,代数方程式,
- f(x) = a0xn + a1xn-1 + ・・・ + an-1x + an = 0
- に関しては,別の方法が存在します.n の値が 2 以下の場合は簡単に解を求めることができますが,3 以上になると,解の公式はかなり複雑になります.さらに,n > 4 の場合は,一般的な解の公式が存在しません.そこで,コンピュータを利用することになります.例えば,ベアストウ法は,対象とする式を,2 次式,
- x2 + px + q
- と (n - 2) 次式の積の形に変換することを繰り返して解く方法です.p と q の値を決めるために,その初期値 p0 と q0 を与え,f(x) を x2 + p0x + q0 で割った余りが 0 になるように,p0 と q0 を徐々に修正していきます.
- 先に述べたように,行列 A の固有値は,
- |A - λI| = λn + b1λn-1 + ・・・ + bn-1λ + bn = 0
- の根となります.従って,b1 から bn の値が決まれば,ベアストウ法によって上式の根(固有値)を求めることができます.フレーム法は,この方程式の係数 b1,・・・,bn を求めるための方法です.
- 後に述べる多変量解析においては,実対称行列の固有値及び固有ベクトルが重要な役割を果たします.実対称行列とは,行列の要素がすべて実数である対称行列( aij = aji,i 行 j 列の要素 = j 行 i 列の要素)であり,固有値はすべて実数となります.実対称行列の固有値及び固有ベクトルは,例えば,ヤコビ法等によって求めることができます.
- 一般の行列に対する固有値及び固有ベクトルを求める方法も存在します.べき乗法は,任意の初期ベクトル v0 から始め,
- vk = Avk-1 / ∥Avk-1∥ k = 0, 1, 2, ・・・
- という手続きを繰り返すと,∥Avk-1∥,及び,vk が,行列 A の最大固有値の絶対値 |λ|,及び,その対応する固有ベクトル v に収束することを利用した方法です(初期ベクトルの与え方によっては,必ずしも最大固有値に収束しない).最大固有値から,順に,複数の固有値,固有ベクトルを求めることが可能です.なお,∥Avk-1∥ は,ベクトル Avk-1 のノルム(大きさ)を表します.
- 数値微分
- 関数 f(x) が,式の形で明確に記述されているときは,その微分(微分係数)を計算することは簡単です.しかし,必ずしもそうでない場合も存在します.そのような場合は,x を少し( Δx )だけ変化させ,そのときの関数の値( f(x+Δx) )から,微分係数の近似値 ( f(x+Δx) - f(x) ) / Δx を計算することになります.この値は,微分の定義に従えば,Δx が小さいほど真の値に近づいていきます.しかしながら,丸め誤差や打ち切り誤差によって,Δx をあまり小さくするとかえって誤差が大きくなります.数値微分を行うときは,この点に十分注意する必要があります.
- 数値積分
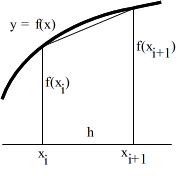
- 関数で区切られた部分の面積や体積を求めるなど,積分も多くの場合に必要とされます.しかしながら,微分とは異なり,積分の場合は,解析的に積分できない関数を扱う機会が多くあります.そこで,関数 f(x) を a から b まで積分したいような場合は,積分の定義に従い,積分区間 [a, b] を n 等分し,右図に示すように,台形の面積の和で近似して計算します.
- 上で述べた方法を台形則と呼びます.台形則では,分割数をかなり多くしないと,十分な精度が得られません.これを改善したのがシンプソン則です.台形則では,各区間において,f(x) を 2 点を通る直線で近似していますが,シンプソン則では,3 点を通る 2 次曲線によって f(x) を近似しています.
- 常微分方程式
- 車や飛行機などの動的システムの運動,簡単な例としては,ボールを投げたときのボールの運動などは,時間の関数 x(t) として表現することができます.しかし,直接その関数を求めることができるわけではありません.一般に,動的システム等を表す微分方程式を求め,その微分方程式を解くことによって求めることができます.「微分方程式モデル」の節でも述べるように,多くの場合,その解を解析的に求めることはできません.そこで,コンピュータを利用することになります.コンピュータによって微分方程式を解く場合,運動を表す関数 x(t) 自体が求まるわけではありません.時間とその時間における関数の値というデータ系列が得られることになります.
- 微分方程式は,
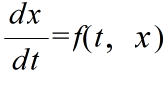
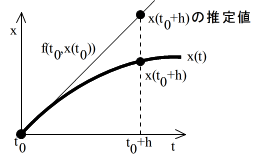
- のように,微分係数の時間的変化として記述されます(この例では,x はスカラー変数とする).微分方程式を解く基本的な考え方は以下に示すとおりです.時刻 t0 における関数 x(t) の値 x(t0) は,分かっているものとします.このときの微分係数(接線の傾き)は,上の式より f(t0, x(t0)) となります.この微分係数より,時刻 t0+h における x(t) の値 x(t0+h) を推定し,それを新しい x(t0) とします.この操作を繰り返すことによって,微分方程式を解くことになります.右図においては,x(t0+h) の推定値と真の値との差が大きくなっていますが,h を十分小さくとれば誤差は小さくなるはずです.この方法をオイラー法と呼びます.
- オイラー法では,t0 における傾き f(t0, x(t0)) だけを利用して,x(t0+h) を推定していますが,ルンゲ・クッタ法では,複数点における傾きを利用しています.その結果,オイラー法より大きな h を使用して,十分な制度で微分方程式を解くことができます.
- 補間法
- 平面上において,2 点 A(x1, y1),B(x2, y2) が与えられたとき,その間にある x3( x1 < x3 < x2 )における y3 の値を推定したいような場合がよく起こります.最も簡単な方法は,点 A,B を直線で結び,直線上の点 C(x3, y3) を利用する方法です.この方法を,線形補間と呼びます.ラグランジュ補間法は,この考え方を拡張し,(n+1) 個の点 (xi, yi) (i = 0, 1, ・・・, n) が与えられたとき,与えられた点を通る n 次多項式,
- f(x) = a0xn + a1xn-1 + ・・・ + an-1x + an
- によって,補間する方法です.ただし,点の数が多ければ,より好ましい補間を実行できると勘違いしないでください.
- スプライン補間法は,与えられた点を通るなるべくなめらかな曲線によって,補間しようとするものです.具体的には,以下のような多項式によって補間します.
- 各区間を,最大次数が m (ここでは,m = 3 とします)である以下に示す多項式( 3 次のスプライン関数)で近似します.
- zi(x) = pi + qi(x - xi) + ri(x - xi)2 + si(x - xi)3 i = 0,1,・・・,n-1
- 与えられた点を通り,かつ,1 階から m 階までの微係数の値が各点ですべて一致するように(つまり,zi(k)(xi+1) = zi+1(k)(xi+1), k = 1, 2, 3),pi,qi,ri,及び,si を決めます(一般に,r0 = rn = 0 とする).
- ベジエ曲線は,上で述べたような補間法とは異なります.つまり,与えられた点を通る曲線を描くのではなく,与えられた点(B0,B1,・・・,Bn)で構成される定義多角形(ベジエ多角形)から,次式によって決まる曲線を描きます.
- P(t) = ΣBiJn , i(t) 0 ≦ t ≦ 1
- ここで,P(t) は曲線上の点の座標であり,t = 0 の時は B0 に,また,t = 1 の時は Bn に一致します.また,Jn , i(t) は,ベジエ基底関数と呼ばれます.たとえば,n = 3 とし,ベジエ多角形を B0 = (1 1),B1 = (2 3),B2 = (4 3),B3 = (3 1) とすると,ベジエ曲線は以下のようになります.
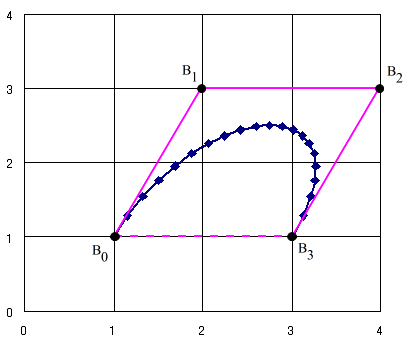
- ベジエ曲線を複数個つなげて,下の図に示すような,複雑な曲線を描くこともできます.従って,曲線部を持つ様々な製品の設計にも利用されます.
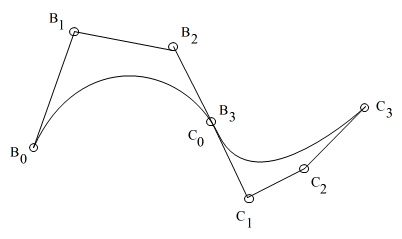
- どのようなシステムであれ,システムを設計する際は,最適なシステムを目指すはずです.従って,システムの最適化は非常に重要な課題です.システムを大きく分類すれば,静的システム(時間を陽に含まないシステム)と動的システム(時間を陽に含むシステム)に分けられます.
- まず,最初に,静的システムの最適化について考えてみます.時間的な変化があり得るシステムであっても,ある固定した時刻におけるシステムの最適化を試みる場合は,静的システムの最適化とみなすことができます.静的システムの最適化を一般的に記述すれば,以下に示すような問題になります.
- 静的システムの最適化:目的関数,
- y = f(x) (1)
- を,制約条件,
- gj(x) ≧ 0, j=1,2,・・・,m (2)
- のもとで,最大にする.
- 最小にする問題も,目的関数の符号を変えれば最大にする問題となりますので,基本的に同じです.静的システムの最適化手法は,対象とするシステムの性質により,以下のように分類されます.
- 線形計画法(LP: Linear Programming)
- f(x) 及び gj(x) がすべて線形である場合.
- 非線形計画法(NP: Nonlinear Programming)
- f(x) または gj(x) に,非線形の式が含まれる場合.
- 組み合わせ最適化(Combinatorial Optimization)
- x の値として,離散的な値だけをとるような式が含まれる場合.似たような問題,または,異なる表現方法として,離散的最適化(Discrete Optimization),組み合わせ計画法(Combinatorial Programming),離散的計画法(Discrete Programming)のようなものがあります.
- 遺伝的アルゴリズム(GA: Genetic Algorithm)
- 幅広い最適化問題に適用可能な方法です.遺伝的アルゴリズムは,最適化問題だけに使用される方法ではありません.また,その他の面からも,上記 3 つの手法と並列的に並べるには問題がありますが,ここではあえて最適化手法の一つとして話します.
- 線形計画法(LP: Linear Programming)
- 次に,動的システムの最適化について考えてみます.システムの時間的な変化を考慮して最適化を行います.例えば,A から B へ向かう飛行機の最短時間経路,燃料を最小にする経路等を求めるような問題が相当します.本来,「制御理論」の範疇で扱われる問題が多くなりますが,ここでは,「制御理論」そのものには言及せず,動的計画法(DP: Dynamic Programming)だけを取り上げます.動的計画法は,必ずしも時間的変化があるシステムの最適化だけを対象にしているわけではありません.かなり幅広い問題に対して適用可能です.詳細に関しては,動的計画法の節を参照してください.
- 線形計画法( LP: Linear Programming )
- 線形計画法を,2 変数の簡単な問題で説明します.変数 x1 及び x2 に対し,以下に示すような最適化問題を考えてみます.
- 目的関数,
- z = 3x1 + 2x2 (1)
- を,制約条件,
- 3x1 + x2 ≦ 9 (2)
- 2.5x1 + 2x2 ≦ 12.5 (3)
- x1 + 2x2 ≦ 8 (4)
- x1, x2 ≧ 0
- のもとで,最大にする.
- 制約条件を満足する領域を図示すると,下図の斜線部分のようになります.したがって,目的関数は,赤線の位置で最大になります.つまり,x1 = 2,かつ,x2 = 3 のとき,最大値 12 となります.
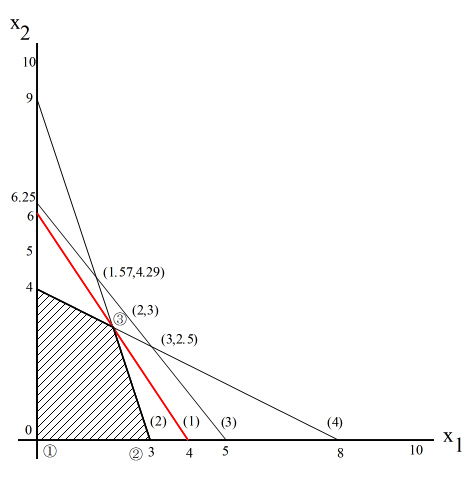
- 変数の数が 3 以上になれば,上で述べたような図による方法は使用できません.そこで登場するのが単体法(シンプレックス法)です.上の図を見てください.制約条件を構成する方程式による交点は複数存在し,目的関数は,いずれかの交点で最大となります.しかし,変数の数が増えれば,その数も膨大になり,それらの点を一つずつチェックすることは大変な作業になります.明らかに,目的関数は,斜線部のいずれかの頂点(交点の一つであり,上図では 4 つ存在)を通る際に最大となります.そこで,単体法では,この制約条件を満たす頂点だけを効率的に探索し,最適解に導きます.
- 非線形計画法( NP: Nonlinear Programming )
- 非線形計画法は,目的関数によって表される地形において,最も高い山の頂上の座標と高さを求めることに相当します.一般に,目的関数で表される地形には複数の山が存在します.非線形方程式の解を求める場合と同様,目的関数と制約条件を与えると,自動的に最も高い山の座標と高さを出力してくれるような方法は存在しません.初期値の与え方によって,異なる結果が得られるのが普通です.
- 制約条件の扱いもかなり面倒です.等式制約条件だけの場合に対しては,ラグランジュの未定乗数法という有名な方法が存在します.それ以外の場合は,ペナルティ関数を利用して制約条件のない問題に変換する方法が良く使用されます.以下においては,制約条件がないものとして話を進めていきます.
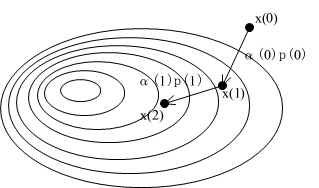
- 最適解を求める方法としては,非線形方程式の解を求める場合と同様,傾き情報(微分)を利用する方法と,利用しない方法が存在します.最初に,利用する方法について,上図に従って説明していきます.まず,初期値 x(0) を与えます.次に,傾き等の情報を利用して次に進むべき方向 p を決め,その方向に α だけ進み,その位置を x(1) とします.x(1) を新たな x(0) とみなし,同様の処理を繰り返します.
- α として一定値を採用する場合もありますが,p の方向で目的関数の値が最大になる点を,1 次元探索手法(黄金分割法,2 次多項式近似による方法)を使用して求め,その位置まで進む方法も良く使用されます.
- 最適解を求める方法として,簡単で,かつ,よく知られた方法に最急降下法があります.最急降下法では,p として最も傾きが急な方向を選び,α は一定とします.最急降下法において,α を 1 次元最適化によって求める方法を,最適勾配法と呼びます.いずれにしろ,収束速度はあまり速くありません.共役勾配法は,p として直行する座標軸の方向を順番に選ぶ方法の変形であり,共役なベクトルの方向を選択します.特別な目的関数に対しては有効な方法です.
- Newton 法(ニュートン法)では,目的関数を探索点 x(k) の近傍で 2 次多項式で近似し,それが最大となる点を次の探索点とすることを繰り返し,最適解を求めます.Newton 法は,解の近傍における収束速度は速いのですが,初期点を解の近傍に取らなければ収束性が保証されません.また,2 階の微分係数からなる Hesse 行列及びその逆行列を毎回計算しなければならず,1 回の繰り返し計算あたりの計算量が多くなります.この逆行列の計算を避けるために考え出されたのが,準 Newton 法です.
- 今まで述べてきた方法は,すべて,傾き情報を利用する方法でした.最後に,傾き情報を利用しないシンプレックス法について説明します.概念的なことを理解してもらうために,2 変数の目的関数
- z = f(x, y)
- の最小値を求める場合について,アルゴリズムの細部は省略して説明します.まず,3 点 A,B,C (初期シンプレックス)を決めます.次に,3 点の内,z の値が最大になる点を選び,その点を他の 2 点から決まる直線に対して対称な位置に移動します.下図においては,点 A が点 D に移動し,新しい三角形 BCD ができます.
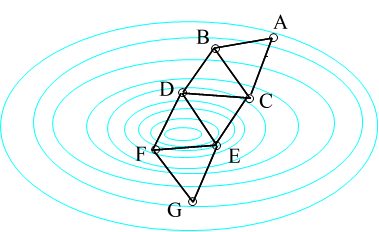
- 同じような処理を繰り返すことによって,
- B → E, C → F, D → G
- のように移動していきます.徐々に,Z が最小となる方向に三角形が移動していくことが分かるかと思います.しかし,このまま続けると,点 G が点 D に移動し,同じ状態を繰り返すことになってしまいますので,そのようなときは,三角形の辺の長さを半分にし,同様の処理を繰り返します.三角形の辺の長さが精度的に適切な値になったときアルゴリズムは終了します.
- 組合せ最適化( Combinatorial Optimization )
- 組合せ最適化の目的は,組み合わせの対象となるものから,最適な組み合わせを選択することです.恐らく,普段の生活の中で最も多く出会う問題ではないでしょうか.対象となるものが少なければ,すべての組み合わせをチェックし,その中から最適なものを選択可能です.しかしながら,組み合わせの数が膨大になる問題が少なくありません.例えば,将棋において,次の一手を,相手の出方を考慮したすべての組み合わせの中から最適な手を選択するといった方法によって決めることはできません.荷物の配送問題などに対応する有名な巡回セールスマン問題(すべての都市を一度だけ訪問した後,最初の都市に戻る最小の経路を求める問題)において,都市の数が 50 であれば,その可能な経路は約 3×1062 通りになり,やはり,すべての経路をチェックすることは不可能です.また,組合せ最適化問題の困難さは,場合の数と共に,微分を使用できないため,どの方向に向かえば最適値に到達できそうかを予測できない点にもあります.
- 他の最適化問題についても同様ですが,実際の問題においては,真の最適解だけが意味を持つわけではありません.最適解に近い解であれば十分役に立つ場合も多くあります.特に,組合せ最適化問題の場合は,解を求めるために時間がかかることもあり,以下に示すような近似解法もよく使用されます.
- 欲張り法 : 目的関数値の良さを示す局所的評価に基づいて,可能解を直接構成していく方法です.
- ランダム法 : 解をランダムに何個か選び,発見された可能解の中で目的関数値が最小のものを選ぶ方法です.
- 反復改善法(逐次改善法) : 何らかの方法で得られた近似最適解に対して,その近傍,つまり少し変更を加えることで得られる他の解を調べ,改善できればそれに置き換えていく方法です.
- 緩和法 : 制約条件を緩和することで一つの解を求め,それに修正を加えて可能解を構成する方法です.
- 分割法 : 与えられた問題をいくつかの部分問題に分解し,それぞれの解から,もとの問題の可能解を合成する方法です.
- 人工知能の分野における問題には,組合せ最適化問題として扱えるものが多く存在します.囲碁,将棋等,ゲームの問題はもちろんですが,有限個の単語の中から,翻訳文として最も適切な単語の組合せを見つける,といった意味から,機械翻訳のようなものも一種の組合せ最適化問題であるといえます.
- 特に,探索の分野は,組合せ最適化を扱っていると言って良いと思います.そこで,探索の分野について簡単に説明します.まず,問題の表現方法について述べます.問題を解く各段階における対象の有様や条件を状態( State )と呼びます.問題を解くということは,与えられた初期状態に,何らかの作用素( Operator )を適用して,目標状態(問題が解かれた状態,最適解であることが望ましい)に持っていくこと,つまり,作用素の系列を見つけることに相当します.
- 初期状態からすべての作用素を適用することにより到達可能な状態の集合を状態空間と呼びます.状態空間を表現するのに,下に示すようなグラフがしばしば使用されます.グラフの各節点(ノード)は状態を表し,また,枝は作用素を表します.節点には状態( s1 等),また,枝には作用素の種類とその作用素を適用する際のコスト(op1,3 等)を明記します.ただし,すべての作用素に対するコストが同じ場合は,コストの表記を省略します.また,下の右図のように,閉路のない連結グラフを木と呼びます.
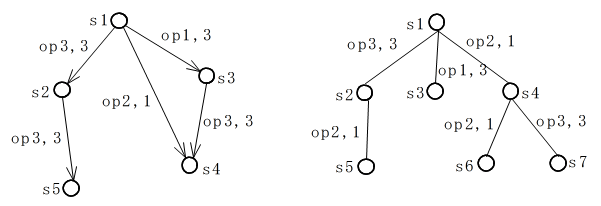
- 問題を解くためには,状態空間内を探索し,最適解を見つければよいわけですが,膨大な空間であるため全空間を探索することが不可能である場合がほとんどです.そこで,有効な探索方法が重要になってきます.基本的な探索方法として横型探索(探索木において,深さが浅い節点から探索),縦型探索(探索木において,深さが深い節点から探索)など,機械的な探索方法がありますが,簡単な問題を除き,実際的な問題には適用できません.探索において最も重要なのは,初期状態を表す節点から開始した後,次に対象とする節点(次にどのような作用素を適用するか)を決めることです.この際に知識が利用されます.有効な知識であれば,素早く目標状態に到達するはずです.
- 遺伝的アルゴリズム( GA: Genetic Algorism )
- 「生物は,交叉,突然変異,淘汰を繰り返しながら,環境に適合するように進化していく」と言われています.環境に適合する度合い(以後,適合度と呼びます)を数値で表せば,進化して生き残った個体の適合度は徐々に大きくなっていくことになります.適合度を最適化問題の目的関数と考えると,目的関数の値が進化と共に徐々に大きくなっていくことになります.つまり,目的関数を最大にするという最適化問題の解に近づいていくことになります.
- そこで,コンピュータ上に仮想生命を生成,かつ,その環境に対する適合度を最適化問題の目的関数に一致させ,進化の過程をシミュレーションすることによって,最適化問題を解くことが可能になります.これが,遺伝的アルゴリズム(GA)によって最適化問題を解く基本的考え方であり,そのアルゴリズムは以下のようになります.
- 初期化
- 適切な数( N 個,集団サイズ)の個体からなる初期集団を発生させ,各個体の適合度を計算しておきます.通常,各遺伝子の値はランダムに決定します.
- 生物集団の評価
- 収束したか否かの判定を行います.判定は,適合度の大きさ,適合度の変化率,世代交代回数などによって行われます.
- 交叉
- 子供を生成する過程です.交叉方法に対しては,問題によって様々な方法が提案されていますが,例えば,1 点交叉法では,ランダムに選択したペアに対し,染色体の切断箇所をランダムに 1 カ所指定し,その箇所(下の例における赤線の部分)で親の遺伝子を交叉させます.
01001|101 01001110 親 → 子供 01100|110 01100101
- 集団内よりランダムに適切な数( M 個)のペア(親)を選択し,設定された交叉確率 Pc (交叉が発生する確率)に従って, 2 * M 個の子供を生成します.
- 突然変異
- ある与えられた確率 Pm(突然変異率)で,突然変異を起こさせます.一般的に,突然変異は,局所的最適解からの脱出に効果があります.しかし,突然変異率を大きくすると,ランダム探索に近い状態になりますので,通常,小さな値が使用されます.問題によって,様々な突然変異方法が考えられています.
- 各個体の評価
- 各個体の適合度を計算します.
- 淘汰
- ここまでの過程により,一般的に,個体数は初期の集団サイズより増加しているはずです.ここで,環境に適合しない個体を淘汰することによって,個体数を初期の集団サイズ N に戻し,世代数 = 世代数 + 1 とし,B に戻ります.単純に考えると,適合度が高いものだけを残せば良いように思えますが,そのようにすると,局所的最適解に陥りやすくなります.そこで,適合度が低い個体もある程度生き残れるような方法が良く使用されます.
- GA は,非線形計画法,組合せ最適化,いずれの方法が対象とする問題にも適用できる方法ですが,非線形計画法が対象とするような問題に対しては,あまり高い精度の解は期待できません.しかし,初期集団として複数の個体を発生するため,複数の初期値に対して解を求める場合と似た効果があり,初期集団の範囲内であれば,大局的な最適解に収束する可能性が強くなります.
- 動的計画法( DP: Dynamic Programming )
- 「決定の全系列にわたって最適化を行うためには,初期の状態と最初の決定がどんなものであっても,残りの決定は最初の決定から生じた状態に関して最適な政策を構成していなければならない」ということを,最適性の原理と呼びます.別の表現をすれば,「最適経路中の部分経路もまた最適経路になっている」ということを意味しています.
- 動的計画法は,この原理を利用して最適化問題を解きます.基本的に,動的システムの最適化に利用される方法ですが,問題を,多段決定問題,つまり,各段における決定の系列を求めるような問題に変換できれば,静的システムの最適化にも利用可能です.例えば,複数の投資先があった場合,限られた資金を,どのように配分して投資するかを決めたいような場合にも利用できます.
- 「決定の全系列にわたって最適化を行うためには,初期の状態と最初の決定がどんなものであっても,残りの決定は最初の決定から生じた状態に関して最適な政策を構成していなければならない」ということを,最適性の原理と呼びます.別の表現をすれば,「最適経路中の部分経路もまた最適経路になっている」ということを意味しています.
- 線形計画法( LP: Linear Programming )
- システムのモデル
- 実際のシステムを作成し,それを用いてそのシステムの評価を行いながら,解析・設計を進めていく方法は,最も確実な方法でしょうが,経済的等の理由から不可能な場合がほとんどであると思われます.対象とするシステムのモデルを作成し,そのモデルに従って,システムの解析,設計等を行う方法が一般的です.
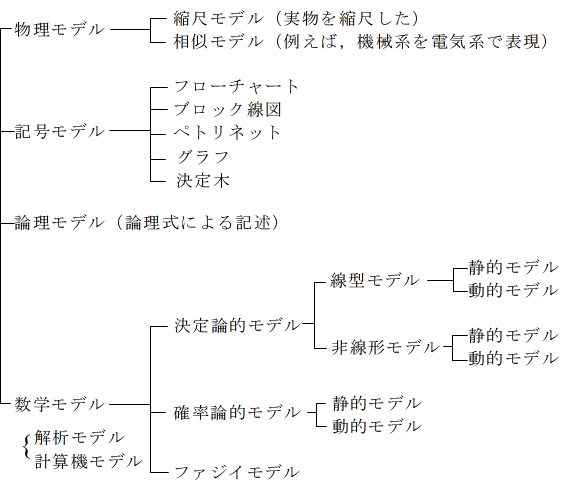
- システムのモデルを作成する方法としては,例えば,上図に示すようなものがあります.ただし,対象とするシステム,また,その目的等によって,モデル化の手法は異なってきます.例えば,エレベータについて考えてみます.エレベータの速度,加速度,停止位置等の制御方法を設計することを目的とするならば,微分方程式モデル(決定論的モデル・線形or非線形モデル・動的モデル)を選択することが多いはずです.
- しかし,あるビルの中に,どのようなタイプ(速度,停止階,大きさ)のエレベータを,何台設置すべきかを検討するような場合,微分方程式モデルでは役に立ちません.例えば,待ち行列モデル(確率論的モデル・動的モデル)などが使用されるはずです.また,エレベータ内部や外部のボタン(目的の階,扉の開閉)が押された場合に対するロジックの設計を行いたい場合は,別のモデルが選択されるはずです.
- ここでは,数学モデルの内,決定論的及び確率論的なモデルの代表である,微分方程式モデル及び待ち行列モデルに関して,その解析モデルと計算機モデル(シミュレーションモデル)について簡単に解説します.
- 微分方程式モデル
- 車や飛行機などの動的システムの運動,簡単な例としては,ボールを投げたときのボールの運動などは,微分方程式によって記述され,それを実際に解くことによって具体的な動きが明らかになります.しかし,ほとんどの場合,微分方程式は非線形になり,解析的にその解を求めることは困難です.従って,ルンゲ・クッタ法など,コンピュータによる解法が重要になります.
- 非線形の微分方程式で表されるシステムであっても,特定の状態及びその近傍だけを対象としてシステムの解析・設計を行うような場合が多くあります.そのような場合は,その状態の近傍においてシステムを線形近似(線形化)し,線形システムとして扱うことができます.一般に,定係数 n 階線形常微分方程式,
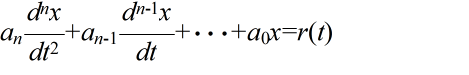
- は,代数方程式(特性方程式と呼ぶ),
- anλn + an-1λn-1 + ・・・ + a1λ + a0 = 0
- の根を求めることができれば,解析的に解くことが可能です.定係数 n 階線形常微分方程式は,適当な変数変換によって,定係数 1 階線形連立常微分方程式,
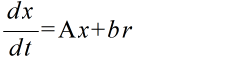
- に変換することができます.上で述べた,特性方程式は,行列 A の固有方程式と一致します.つまり,特性方程式の根は,行列 A の固有値となります.
- 例えば,定係数 2 階線形常微分方程式において,特性方程式は 2 次方程式となり,r(t) = 0 の場合に対する一般解は,2 次方程式の根によって以下に示すような形になります.
- 異なる 2 実根 m1,m2 x(t) = c1em1t + c2em2t
- 重根 m x(t) = emt + temt
- 虚根 α±iβ x(t) = c1eαt sin(βt + c2)
- このように,定係数 n 階線形常微分方程式の解は,特性方程式の根(行列 A の固有値)の影響を強く受けます.
- 待ち行列モデル
- 待ち行列モデルも,先に述べたエレベータシステムだけでなく,電話通信システム,計算機システム,輸送システム(道路,鉄道,航空),工場や機械の保守・サービス,在庫・生産システム等,様々な分野で利用されています.待ち行列モデルの基本は下の図に示すようなシステムです.
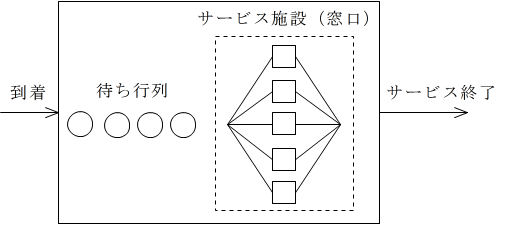
- このシステムを表現するのに,以下に示すような,ケンドール記号がよく使用されます.
- X / Y / s(N) : ケンドール記号
- X, Y : 到着分布とサービス分布を表す.分布により,以下の記号を使用する.
- M : 指数分布
- En : n 相アーラン分布
- G : 一般分布
- D : 一定分布
- s : 窓口の数
- N : システムの容量(待ち行列の許容最大長,∞のときは省略可能)
- 非常に簡単なモデルの場合は,微分方程式のように,待ち行列モデルを記述する確率微分方程式を導出することが可能ですが,実際上,不可能である場合がほとんどです.そこで,待ち行列システムの解析手段としては,モンテカルロ法的なシミュレーションに頼る以外方法はありません.モンテカルロ法とは,乱数を取り扱う技法の総称です.また,乱数とは,ある指定された確率分布を持つ数列であり,計算機では,近似的にランダムな数列を発生させることによって作成します.このようにして生成された乱数を,疑似乱数と呼びます.
- 微分方程式モデルのように,動的なシステムをシミュレーションする場合は,コンピュータ内部で時間を進めていく必要があります.微分方程式モデルでは,刻み幅という形で,一定時間毎に時間を進めていきました(ルンゲ・クッタ法).
- しかし,待ち行列システムの場合はどうでしょうか.例えば,自動券売機を何台設置すべきかをシミュレーションによって決めたいとします.このとき,時間を進める基本単位である刻み幅をどの程度にすればよいでしょうか.かなり小さくしないと,たくさんの人がほぼ同時に券売機に殺到したような場合に,適切な処理を行うことができません.しかし,誰も来ないときは,システムの状態が変化しないため計算をする必要が無いにもかかわらず,無駄な計算を頻繁に行わなければ成りません.
- 待ち行列システムのように,何か事象(客の到着,サービスの開始・終了等)が発生しない限り状態が変化しないようなシステムを事象駆動システムと呼びます.このようなシステムでは,時間を一定毎に進めず,事象が発生した時点へ次々と時間を進めていく方法がとられます.つまり,次に発生する事象の内,最も早く発生する事象を調べ,その時点まで時間を進め状態の変更等何らかの処理を行うといった方法です.この方法に従い,待ち行列システムをシミュレーションするためのフローチャート例を以下に示します.
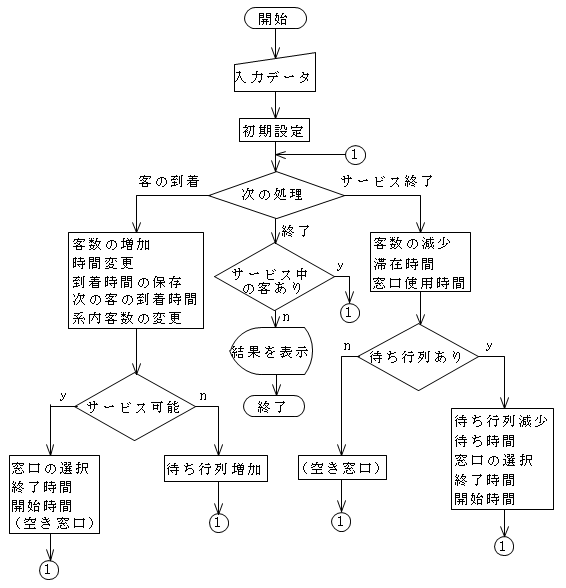
- ある商品を売ろうとした場合,それが売れるまではある程度の量をどこかに保管しておく必要があります.お客さんが来ても売るべき商品が無いような状態では,せっかくの商機を失うことにも成りかねません.しかし,保管するには,場所や費用がかかります.また,保管期間によって,商品価値が無くなるものも少なくありません.このように,「どの程度の在庫を持つべきか」,「何時,どのくらいの量を発注すべきか」等の問題を扱うのが,在庫管理の分野です.物流関係のシステムを作成しようとする場合は,当然,在庫管理の基本的概念程度は理解しておくべきです.
- 在庫管理問題を扱う当たって考慮しなければならない要因として以下のようなものがあげられます.
- 発注費,生産段取り費: K
- 商品の在庫管理の場合,発注量の多少に関わらずかかる費用を発注費といいます.例えば,通信費,書類作成費等がこれに当たります.また,製品の在庫管理の場合は,生産量の多少に関わりなくかかる費用に相当し,生産段取り費と呼びます.例えば,工作機械の再設定(部品の取り替え,ソフトの入れ替え等)に必要な時間・費用等がこれに当たります,
- 購入単価,生産費用: c
- 商品 1 単位を購入する費用(仕入れ価格,保険料,梱包費等)を購入単価,また,製品 1 単位を生産するために必要な価格(材料費,光熱費等)を生産費用と呼びます.
- 販売価格: p
- 商品または製品 1 単位を販売する価格です.
- 品切れ損失: s
- お客さんが来たとき,お客さんが買いたい商品が品切れであれば,せっかくの得られるべき利益を無駄にしてしまいます.この損失は,必ずしも,一時的なものに留まりません.店の信用を失い,二度と来店してくれないようなことになれば,将来的に大きな損失を生むことになります.
- 在庫保持費用: h
- 1 単位の商品・製品を,1 単位期間保管するために必要な費用です.この中には様々なものが含まれます.最も直接的なものは,倉庫の維持・管理費です.その他,保管することによる商品価値の低下もこの中に含まれます.また,在庫量に相当する金額を持っていれば,投資等によって利益が得られる可能性がありますが,在庫の状態では全く期待できません.このようにして失った利益もここに含まれます.
- 発注費,生産段取り費: K
- 在庫管理問題はいくつかのタイプに分類できます.まず,需要が確定しているか否かによって分類可能です.基本的に,需要が確定した方が問題は取り扱いやすくなります.また,ある時点の発注量が他の時点における発注量の影響を受けるか否か(従属的,または,独立的)によっても分類できます.他の時点における発注量の影響を受ける場合(従属的)とは,例えば,残っている在庫量によって,次回の発注量が影響を受ける場合です.また,独立的な場合とは,新聞少年の例のように,前回発注して残ったものはすべて廃棄してしまうため,次回の発注量に影響を与えないような場合です.ここで影響というのは,在庫量による影響であり,「前回は多く発注しすぎたから,次回はもう少し減らすか」といった形で現れる影響は考慮しません.
- スケジューリング問題は,工場等での仕事のスケジュール,建設工事やソフトウェア開発などのプロジェクトスケジュール,バス・列車・航空機等のダイヤと乗員のスケジュール,要員(工場の作業者,病院の医師・看護婦等)のスケジュール,宅急便・郵便・ごみ等の集配スケジュール,大学・予備校等の時間割/教室割スケジュール等,様々な分野で発生します.
- 繰り返し型スケジューリング
- 工場(ショップ:shop)において,所要時間や納期遅れが最小になるように,各仕事(ジョブ:job)を各機械でどのような順序で加工すべきかを決めることは,非常に重要な問題です.仕事がすべて同じ機械順序で加工を受ける場合をフローショップ問題( Flow Shop Problem ),また,仕事によって機械の処理順序が変化して良い場合をジョブショップ問題( Job Shop Problem )と呼びます.
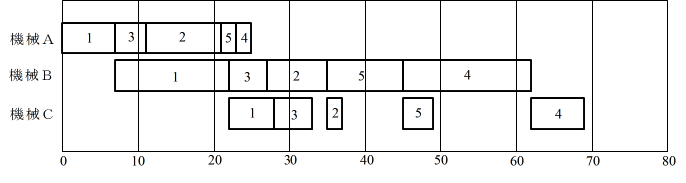
- 例えば,典型的なフローショップ問題として以下のような問題があります.5 つの仕事があり,各仕事に対する各機械での加工時間は決まっており,仕事は,すべて,機械 A → B → C の順序で加工されるものとします.このとき,総所要時間や総納期遅れを最小にするように,例えば,以下の図(ガントチャート,横軸は時間)に示すような加工順序を決めることになります.残念ながら,フローショップ問題やジョブショップ問題に対する,一般的な解法は存在しません.特別な問題に対する解法,近似的な解法,または,組み合わせ最適化において述べた各手法を利用することになります.
- プロジェクトスケジューリング(PERT/CPM)
- プロジェクトスケジューリングの手法には,PERT と CPM という 2 つの有名な方法があります.PERT は,1957~1958 年に,米国海軍,Booz, Allen and Hamilton 社,ロッキード社が共同でポラリスミサイルシステムの効率的開発のために考案したものであり,時間管理のみを考慮しています.また,CPM は,デュポン社とレミントン・ランド社が化学プラントの保全管理のため開発したものであり,費用の概念を強調しています.
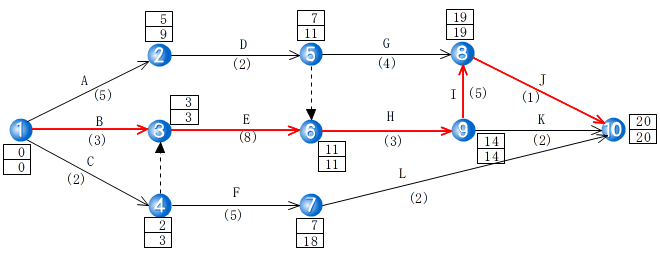
- PERT ネットワークの例を以下に示します.矢印上に書かれたアルファベットは作業,また,カッコ内の数字は作業時間です.なお,各結合点近傍に書かれた四角の中の上の数字は,最早開始時刻と呼ばれ,時刻 0 にプロジェクトを開始したとき,ある結合点に最も早く到達可能な時刻,つまり,ある結合点に至るすべての作業が完了している最も早い時刻を示します.また,上の数字は,最遅完了時刻と呼ばれ,結合点 i を始点とする作業 pij によって結合されているすべての結合点 j へ,最早開始時刻前に到達するために,結合点 i に到達していなければならない時刻です.最早開始時刻と最遅完了時刻が一致した結合点を結んだパスを.クリティカルパス(赤い線)と呼びます.クリティカルパスは,プロジェクトの総作業時間を決めるものであり,クリティカルパス上の作業の遅れは,全体の遅れに直接響くことになります.
- 過去の時系列データから,将来を予測したいような場合がしばしば起こります.最も簡単な方法は,過去のデータの平均値を使用する方法です.平均値を利用する方法としては,以下のような方法があります.なお,以下の説明において,di を過去,または,新しく得られたデータ,Di を予測値とします.
- 単純平均法
- 過去のデータ,
- di i = 1, 2, ・・・, n
- の平均値,
- D = Σ di / n
- によって,予測する方法です.
- 移動平均法
- 時間の経過と共に,平均の対象とするデータを徐々に変更していく方法です.例えば,3 つのデータを平均する場合は,以下のようになります.
- d1, d2, d3 → D4 = (d1 + d2 + d3) / 3
- d2, d3, d4 → D5 = (d2 + d3 + d4) / 3
- ・・・・・
- 簡易指数平均法
- 時間の経過と共に,対象とするデータに重みを付けて平均を取っていく方法です.具体的には,以下の式に従って,予測値を計算します.
- 新予測値 = α (新しいデータ) + (1 - α) (旧予測値)
- 例えば,以下のようにして計算します.
- D1 = d1
- D2 = α d2 + (1 - α) D1
- D3 = α d3 + (1 - α) D2
- ・・・
- α の値としては,最初,0.3 前後を使用し,落ち着いた時点で再設定をするという方法が良く使用されます.
- 単純平均法
- データに直線を当てはめ,その直線を使用して予測する方法も存在します.過去のデータ,
- x1 y1
- x2 y2
- ・・・
- xn yn
- から,これらのデータに最も合う直線,
- y = ax + b (1)
- を求め,得られた直線から予測を行う方法です(この直線を,回帰直線と呼びます).直線を決めるために,最小 2 乗法が使用されます.最小 2 乗法は,誤差の 2 乗の和,
- s = Σ (yi - axi - b)2
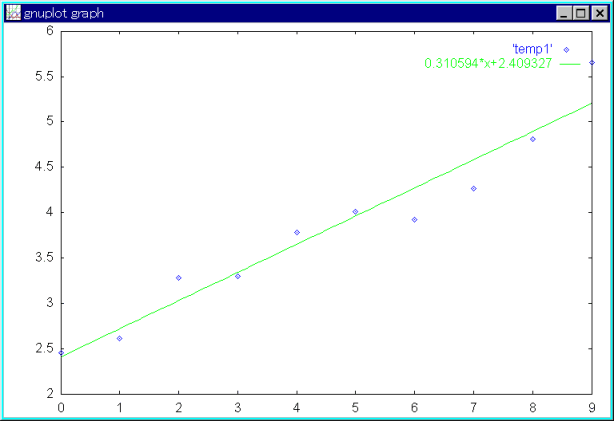
- を最小にするように,(1) 式の a, b を決定する方法です.例えば,点を過去のデータとすると,下の図に示すような直線が得られます.
- 意思決定とは,将来の状態を予測し,最適な結果が得られるように,取るべき行動を決定することです.現実においても,そのようなことが様々な場面で発生すると思います.もちろん,その際,ここで述べているようなことをそのまま適用するようなことはできないでしょうが,何らかの参考にはなると思います.意志決定は,将来における状態の性質や予測可能性によって,以下のようないくつかのタイプに分類できます.
- 将来の状態が確定的である場合
- 通常の最適化問題となります.
- 将来の状態が確率的で,かつ,その分布が既知である場合
- どのような行動を取ったら,どのような結果になるか(どのような利得が得られるか)を,将来の状態毎に表した表を利得表と呼びます.分布が既知ですので,各利得を得られる確率も計算可能です.このとき,以下のような方法で,取るべき行動を決定します.
- 期待値基準 各行動に対し,獲得可能な利得の期待値を計算し,その最大のものを選択します.
- 満足度基準 満足度を,ある行動をとったとき S 以上の利得を得られる確率と定義し,満足度を最大にするような行動を選びます.
- 将来の状態が確率的で,かつ,その分布が未知である場合
- 利得表に基づき,以下に示すような方法で,取るべき行動を決定します.
- ラプラス基準 すべての状態が同じ確率で実現するとみて,期待値を計算し,その最大のものを選びます.
- ミニ・マックス(マックス・ミニ)基準 結果が費用の場合は,起こりうる最大の損失を最小にするような,また,結果が利得の場合は,起こりうる最小の利得を最大にするような行動を選択します.
- マックス・マックス(ミニ・ミニ)基準 常に最良の状態が実現すると信じて行動を決定する方法です.結果が費用の場合は,起こりうる最小の損失を最小にするような,また,結果が利得の場合は,起こりうる最大の利得を最大にするような行動を選択します.
- ハーウィツ基準 ミニ・マックス(マックス・ミニ)基準とマックス・マックス(ミニ・ミニ)基準の折衷案です.2 つの方法の重み付き平均値を最大にするような行動を選択します.
- サーベジュのミニ・マックス落胆基準 落胆を,各状態から得られる最良の結果と実現した結果との差として定義します.結果が費用の場合は,各状態に対する費用から同じ状態の最小の費用を引いたものに,また,結果が利得の場合は,ある状態の最大の利得から同じ状態に対する利得を引いたものになります.起こりうる最大の落胆を最小にするような行動を選択します.誤った行動を選択したときの責任が重要である場合に用いられます.
- 将来の状態が競争相手によって決まり,競争相手の行動を予測できない場合
- このタイプの問題としてゲームの理論があります.
- 信頼性
- システムの性能が如何に優れていても,故障を繰り返しほとんど動かないようでは全く役に立ちません.そこで,システムの信頼性という考えが非常に重要になってきます.信頼性( Reliability )は,「アイテムが与えられた条件で規定の期間中,要求された機能を果たすことができる性質」,また,信頼度( Reliability )は,「アイテムが与えられた条件で規定の期間中,要求された機能を果たす確率」と定義されます.なお,システムの信頼性(信頼度)は,以下のような項目で評価されます.
- 故障率( Failure Rate ) λ(t)
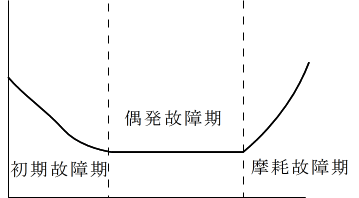
- 単位時間内に故障する割合です.故障率は,一般に,以下に示す 3 つの段階を経て変化し,上図のような形をしています.この曲線を,バスタブ曲線と呼びます.
- 初期故障期 初期不良が主たる故障の原因となっている期間です.故障率は時間と共に減少します.
- 偶発故障期 故障率は一定,つまり,λ(t) = λ となる期間です.
- 摩耗故障期(疲労故障期) 故障率は時間と共に増加し,寿命を迎える期間です.
- 平均故障時間( MTBF: Mean Time between Failures )と平均寿命( MTTF: Mean Time to Failures )
- 故障が発生するまでの動作時間の平均です.修理が可能なものに対しては MTBF,修理が不可能なものに対しては MTTF と呼ばれます.故障率が一定値 λ の時は,1 / λ となります.
- 平均故障回復時間(平均修理時間,MTTR: Mean Time to Repair)
- 修理にかかる平均時間です.
- 稼働率( Availability )
- システムがある期間内において運転されている時間の割合です.
- 保全度( Maintainability )
- 故障が発生してから修理する,または,故障が発生することを防止するために点検,部品の交換を行う保全作業期間の占める割合を言います.
- 耐用寿命( Length of Operating Period)
- システムを使用できる期間のことで,耐用寿命には,装置が摩擦や腐食などにより使用不可能となる寿命のほかに,システムそのものが技術の進歩に取り残されて陳腐化し,装置としては運転可能であっても,性能的にみて著しく時代遅れとなり使用できない場合も含まれます.
- 信頼性とシステムの構造
- 複雑なシステムの場合,システムの信頼度は,サブシステムの信頼度から計算されます.その際,システムの構造によってその計算方法は異なってきます.基本的なシステム構造は以下に示すとおりです.
- 直列システム

- サブシステムが直列に接続されることによって構成されているシステムです.したがって,システムが正常に動作するためには,各サブシステムがすべて正常に動作している必要があります.例えば,信頼度が Ri(t) であるサブシステムを n 個直列に接続した場合,システムの信頼度は以下のようになります.
- 信頼度 R(t) = R1(t)・R2(t)・・・Rn(t)
- 並列システム
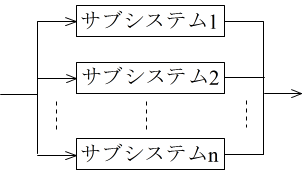
- サブシステムが並列に接続されることによって構成されているシステムです.したがって,システムが正常に動作するためには,各サブシステムのいずれかが正常に動作していれば良いことになります.このようなシステムを冗長システムと呼びます.2 つのシステムに全く同じ処理を同時に実行させ,それらの結果を照合し,結果の正しさを確認しながら処理を進めるデュアルシステムは,その一例です.例えば,信頼度が Ri(t) であるサブシステムを n 個並列に接続した場合,システムの信頼度は以下のようになります.
- 信頼度 R(t) = 1 - (1 - R1(t))・(1 - R2(t))・・・(1 - Rn(t))
- 信頼性向上を目的としたシステム
- 待機システムとは,サブシステムのいくつかを使用せず待機させておき,常時使用しているサブシステムが故障したとき,待機させているサブシステムと切り替えるシステムをいいます.コンピュータシステムにおけるデュプレックスシステムは,その一例です.デュプレックスシステムでは,2 組のシステムを用意し,1 組は稼働状態,他の 1 組は待機状態にしておきます.もし,稼働状態のシステムが故障した場合は,待機状態のシステムを稼働させることになります.待機方法には,ホットスタンバイとコールドスタンバイという 2 つの方式があります.ホットスタンバイ方式は,待機システムにおいても前もって稼働システムと同じプログラムを動作させておき,稼働システムに故障が起こったとき即座に切り替える方式です.また,コールドスタンバイ方式は,稼働システムに故障が起こってから,待機システムに稼働システムが実行していたプログラムを起動して切り替える方式です.
- 信頼性を高めるためには,ハード面,及びソフト面の両面にわたった信頼性設計が重要となります.構成部品の信頼度を上げて故障が発生しないようにするという考え方をフォールトアポイダンスといいます.逆に,障害の発生を見越して,例え故障が発生しても,システム全体としての機能を失わないようにする考え方をフォールトトレラントといいます.フォールトトレラントを実現する方法としては以下に示すようなものがあげられます.
- フェイルセーフ: 故障が発生した場合,常に安全な状態に移行するといった考え方(安全性重視)であり,例として,「石油ストーブを倒すと消える」,「信号機が故障したら,信号を赤にする」などがあげられます.
- フェイルソフト: システムの一部に障害が発生した場合,故障した個所を切り離すなどの操作によって,例え機能を低下させてもシステムの稼動を続けるといった考え方(継続性重視)であり,例として,「停電が発生したら,バッテリー電源に切り替える」などがあげられます.
- フールプルーフ: 利用者が操作や手順を間違えても,誤動作が起こらないようにするという考え方であり,例として,「ファイルを削除する場合に,警告メッセージを出す」などがあげられます.
- 変量(変数)の数が少ない場合,例えば,2 変量の場合は,得られたデータを平面上にプロットし,その様子を眺めるだけで,2 つの変量間の関係をつかむことができます.しかし,変量の数が多くなれば,このような方法を使用できません.多変量解析法とは,互いに関係のある多変量(多変数,多種類の特性値)のデータが持つ特徴を要約し,かつ,目的に応じて総合するための手法です.
- 重回帰分析
- N 組のデータ,
- (yi, xi1, xi2, ・・・, xin) i = 1, 2, ・・・, N
- が与えられたとき,これらのデータを元にして,y の値を,x1, x2, ・・・, xn の線形結合,
- y = b0 + b1x1 + b2x2 + ・・・ + bnxn
- によって予測する方法を重回帰分析と呼びます.b0,b1,・・・,bn の値は,予測の節で述べた回帰直線と同様,誤差の 2 乗の和,
- s = Σ (yi - b0 - b1x1i - b2x2i - ・・・ - bnxni)2
- を最小にするように決定されます.
- 正準相関分析
- 3 変数以上が存在したとき,2 変数間同士の関係は相関係数によって知ることができます.しかし,いくつかの変数の組同士の関係を,変数間同士の関係だけから推論することは非常に難しくなります.例えば,q 個の変数が存在したとき,それらの変数の r 個の組と,残りの (q - r) 個の組との関係を得たいような場合です.正準相関分析は,このような場合に使用される方法です.今,q 個の変数,
- x1, x2, ・・・, xq
- で表されるデータがあったとします.このとき,
- r 個の変数の組: x1, x2, ・・・, xr
- s(= q - r ≧ r)個の変数の組: xr+1, xr+2, ・・・, xr+s
- を考え,それらの線形結合から成る 2 つの変数,
- y = a1x1 + a2x2 + ・・・ + arxr
- z = b1xr+1 + b2xr+2 + ・・・ + bsxr+s
- を考え,y と z との間の関係によって,2 つの組間の関係を見ることにします.ただし,y と z との間の相関係数 ryz を最大にするように上式の各係数を定めるものとします.このようにして得られた変量 y, z を正準変量,また,その各係数を正準相関係数と呼びます.なお,これらの変量は,変数 x1, x2, ・・・, xq から得られる分散共分散行列の固有値及び固有ベクトルと深い関係があります.
- 主成分分析
- 今,以下に示すように,p 個の変量に対して,各 N 個のデータが得られたとします.
- 変量: x1, x2, ・・・, xp
- N 個のデータ: x1i, x2i, ・・・, xpi i = 1, 2, ・・・, N
- これらの変量には,互いに何らかの関係があったとします.このとき,これらのデータの変動に与える因子を一つの変量に要約し,その特徴を把握しようとするのが主成分分析です.
- 主成分分析では,影響を与える変量を,p 個の変量の線形結合,
- z = a1x1 + a2x2 + ・・・ + apxp = aTx
- ただし,a = [a1 a2 ・・・ ap]T,x = [x1 x2 ・・・ xp]T
- で表し,∥a∥ = 1 ( a の大きさが 1 )の条件の下で,z の分散が最大になる( z の変動が最も大きくなる)ように a の値を決めます(これを,a1 とする).このようにして決定された a1 の各要素の値を a11, a12, ・・・, a1p としたとき,
- z1 = a11x1 + a12x2 + ・・・ + a1pxp
- を,第 1 主成分と呼びます.同様に,∥a∥ = 1 で,かつ,z1 とは無相関な z の内で,最大の分散を持つ
- z2 = a21x1 + a22x2 + ・・・ + a2pxp
- を第 2 主成分と呼びます.以下,同様に,第 3 主成分以下も定義されます.なお,変量 x1,・・・ ,xp に対する分散共分散行列の固有ベクトルを,固有値が大きい順に求めていけば,それらが,第 1 主成分,第 2 主成分,・・・,となります.
- 因子分析
- 因子分析は,主成分分析と非常に似ています.主成分分析は,データの変動に与える因子を一つの変量に要約し,その特徴を把握しようとするのです.しかし,一般に,データ内には誤差が存在します.そこで,因子分析では,その誤差を除去して因子を抽出しようとします.ここでも,与えられたデータに対する分散共分散行列の固有値及び固有ベクトルが重要な役割を果たします.
- 判別分析
- 2 種類の集団に対して,複数の変量(n 個とする)に対するデータが得られていたとします.このとき,新しく得られたあるデータ x に対して,このデータがどちらの集団に属するのか判別したいような場合に使用されるのが判別分析です.例えば,「複数の検査データに基づき,病気の有無の判別」,「クレジットに対する申込者のデータから,クレジットカードを発行可能か否かの判別」等に利用されます.判別分析では,誤った判断(集団 1 に属しているのに,集団 2 に属していると判断するような場合や,または,その逆の場合)を行う確率をできるだけ小さくするように判別します.
- クラスター分析
- クラスター分析は,与えられたデータを,それらの間の類似度や距離を基準として,いくつかのグループに分類するための手法です.2 つのデータ間の類似度や距離は,様々な方法で定義可能です.また,データの性質(連続量,離散値,・・・)によっても異なります.そのため,クラスター分析の方法も複数存在します.また,クラスターを構成する方法も,階層的に構成していく方法と非階層的に構成していく方法とがあります.
- 分散分析
- 分散分析は,今まで述べた多変量解析とは多少目的が異なります.その目的からいえば「確率と統計」の検定の箇所で述べた方が良いかもしれません.なぜなら,分散分析が平均値の差の検定の拡張になっているからです.例えば,同じ製品を複数の工場で生産する場合を考えてみて下さい.各製品の特性(大きさ,重さ,性能を表す数値等)や不良率などのデータは,工場毎に異なってくる可能性があります.また,複数の組織(例えば,学科)に対して同じアンケートを実施した場合も,その結果がすべての組織で同じであるとは限りません.工場や組織の数が 2 である場合は,平均値の差の検定を利用して,工場や組織間の平均値の差が有意なものであるか否かを検定することができますが,3 以上の場合は困難になります.さらに,平均値の差の検定においては,差を生む出す要因まで分析対象にすることができません.そのような場合に使用されるのが分散分析です.
- 分散分析において,工場や組織のように結果に影響を及ぼすと考えられる要因を因子,工場や組織の違いを因子の水準と呼びます.工場や組織の違いなど,因子の数が 1 種類である場合に対する方法を一元配置法といいます.また,薬の種類と対象とする動物を変化させて,その効果を調べたいような場合は,因子の数が 2(薬の種類,動物の種類)になります.このような場合に対する方法を二元配置法といいます.
- 脳の中には多数のニューロン(神経細胞)が存在しています.各ニューロンは,多数の他のニューロンから信号を受け取り,また,他の多数のニューロンへ信号を受け渡しています.脳は,この信号の流れによって,様々な情報処理を行っています.この仕組みをコンピュータ内に実現しようとしたものがニューラルネットワークです.なお,ニューラルネットワークによって行われる基本的な処理は,入力として与えられる対象の分類です.
- 基本構造
- 構造
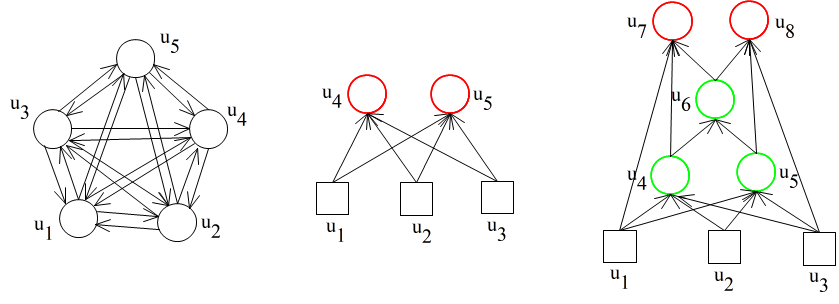
- 上の図は,ニューラルネットワークの典型的な構造を示したものです.これらの図において,円や四角は一つのニューロンに対応し,また,矢印が付いた枝は信号の流れを表しています.
- 左の図は,相互結合ネットワークを表し,また,中央と右の図は,階層的なネットワークを表しています.四角で書かれたユニットは,入力ユニットと呼ばれ,外部からの信号を受け取ります.また,赤いユニットは,出力ユニットと呼ばれ,外部へ信号を出力します.なお,相互結合ネットワークの場合は,すべてのユニットが,入力ユニットと出力ユニットを兼ねるケースが多く見受けられます.
- 中央及び右図のように,多層構造になっている場合,入力ユニットから構成されている層を入力層,また,出力ユニットから構成されている層を出力層と呼びます.右図の中間にあるユニット(空色のユニット)は,隠れユニットと呼ばれ,その層は,隠れ層(中間層)と呼ばれます.
- ユニット
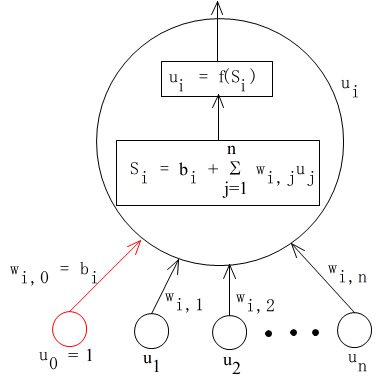
- あるユニット ui を拡大すると,上図のようになります.ユニット ui は,複数のユニット uj ( j = 1, 2, ・・・, n )から情報を入力し(受け取り),何らかの処理をした後,情報を出力します.各ユニットにおける処理は以下のようになります.まず,入力値を元に,以下の値を計算します.
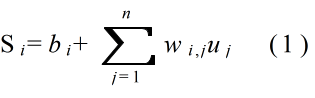
- ここで,
- bi : ユニット ui のバイアス
- wi,j : ユニット uj からユニット ui に与える影響の強さを表し,重みと呼ばれる
- uj : ユニット uj の出力値
- とします.(1) 式によって計算された Si をもとに,ユニット ui の出力値が以下のようにして計算されます.
- ui = f(Si)
- ここで,関数 f(x) として,例えば,以下のようなものが使用されます.
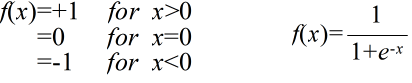
- 学習
- ニューラルネットワークを作成しただけでは,入力ユニットにデータを与えても,出力ユニットから出る値が適切なものである可能性はほとんどありません.何らかの方法で,ユニット間を繋ぐ枝の重み(バイアスも含む)を調整し,希望する出力が得られるようにしてやる必要があります.このことを行うのが,学習です.
- 学習方法には,大きく分けて 2 つの方法があります.それは,教師付き学習と教師無し学習です.教師付き学習は,幾つかの学習例と各学習例に対する目標出力を与え,目標出力と実際の出力が一致するように重みを調整する方法です.また,教師無し学習では,学習例からコンピュータ自身が何らかの基準に基づき重みを調整します.
- 構造
- パーセプトロン
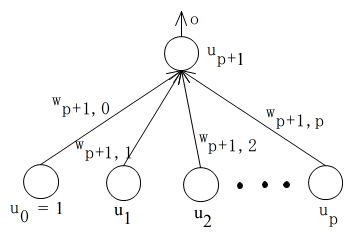
- まず,最初に,最も古典的なネットワークであるパーセプトロンについて説明します.パーセプトロンは,上図に示すように,入力層と出力層だけから成る 2 層のネットワークです.また,入力ユニットの数(p 個)は任意ですが,出力ユニット( p+1 番目が出力ユニット)は 1 つだけです.パーセプトロンは,対象を 2 つに分類しますが,正しく分類できるのは,線形識別関数で分類できる場合だけです.平面上の対象でいえば,対象を直線で分類できる場合です.
- 学習例を繰り返し与え,誤って分類した場合は,重みをある規則に従って修正するといった方法を繰り返すことによって学習を実行します.
- バックプロパゲーション
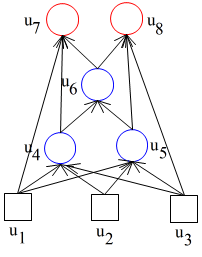
- バックプロパゲーションモデルは,右図に示すように,入力層,隠れ層(複数可能),及び,出力層から成る多層のネットワークです.一般に,出力層のユニット数が,入力層に与えられたパターンを分類する数に相当します.ある層のユニットから,それより上にある任意の層のユニットへ接続することは許されますが,同じ層にあるユニットや下の層にあるユニットへの接続は許されません.
- tpj を,パターン p に対する出力ユニット j の目標出力,opj をパターン p に対する実際の出力ユニット j の出力としたとき,訓練例(パターン) p に対する二乗誤差,
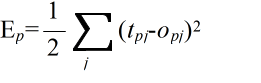
- を最小にするように枝に付加された重みを学習によって修正します.
- 深層学習(ディープラーニング)
- 深層学習(ディープラーニング,Deep Learning )とは,今まで述べたような特定の構造,学習方法を意味するネットワークではありません.一般的に,複数の隠れ層を有したネットワークであり,入力層に与えられたパターンを分類することを目的としています.学習方法として,バックプロパゲーション及びその修正版を使用するネットワークが多く見られますが,ネットワークの構造自体を工夫したニューラルネットワークも存在します.
- バックプロパゲーションモデルに対しては,特にユニットや隠れ層が多くなってきた場合,収束の遅さや不安定さ,過学習の問題等が指摘されてきました.バックプロパゲーションにおいては,訓練例 p が与えられる度に,二乗誤差(コスト関数)を最小にするように,重みやバイアスの修正が行われます.しかし,数万,数十万の訓練例が与えられた場合は,これは大変な作業になります.そこで,深層学習においては,一般に,確率的勾配降下( Stochastic Gradient Descent )という方法が採用されています.さらに,ユニットの出力が 0 や 1 に近づくと収束が遅くなることを避けるために,クロスエントロピー( Cross-Entropy )コスト関数を使用したり,下段の隠れ層の収束速度を上げるため,重みの初期化に対する工夫が行われています.
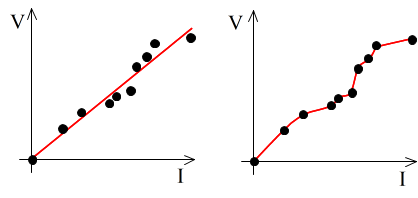
- 過学習( Overfitting )とは,例えば,以下に示すような問題です.オームの法則,電圧 = 抵抗 × 電流( V = RI )を機械に学習させたいとします.ある抵抗 R に加える電圧 V を変化させ,そこに流れる電流 I を測定すれば,測定誤差等のため,上図の点で示したようなデータが得られるはずです.これらのデータから,上図の左に示した赤色の直線の傾き R と y 切片を学習することが目的になります.しかし,ニューラルネットワークは変更可能なパラメータ(重みとバイアス)を多く持ち,すべての点を正確に通る多項式の係数を学習するような結果に陥りがちです(上図の右).これが,過学習です.
- 過学習を防ぐ一つの方法は,ユニットや隠れ層の数を減らすことです.しかし,ユニットや隠れ層の数が多いほど,ニューラルネットワークの表現能力は高いと言われており,極端に減らせば,学習能力自身を失いかねません.そこで,深層学習では,訓練例を増やす方法を採用しています.少し前までは,大量の訓練例を使用して学習させることは困難でしたが,最近では,GPU ( Game Processing Unit )を使用した並列計算の利用によりパソコンでも実行可能になっています.
- そのほか,過学習を防ぐために,様々な方法が考えられています.例えば,コスト関数に重みの 2 乗和から成る項を加える方法( Weight Decay,L2 Regularization ),重みの絶対値の和からなる項を加える方法( L1 Regularization ),ドロップアウト(隠れ層のいくつかのユニットをランダムに選択し,それらのユニットを一時的に削除して学習を実行する.このサイクルを繰り返した後,最終的には,すべてのユニットを結合させる)などの方法があります.さらに,十分な量の訓練例が得られない場合は,既存の訓練例を人為的に多少修正したもの,例えば画像認識の場合は,元の画像を多少回転したものなど,を訓練例に追加して訓練例を増加させる方法も良く使用されています.
- 深層学習は,多くの分野で目覚ましい成果を上げています.コンピュータの知能が人間の知能を上回ったなどと言う人もいます.しかし,本当にそうでしょうか.計算や記憶といった分野では,コンピュータの能力は既に人間の能力を遙かに上回っています.計算能力や記憶能力も,人間の知能の一部です.しかし,これだけの能力で,コンピュータの知能が人間の知能を上回ったとは誰も言いません.
- 深層学習から出力される結果を見れば,明らかに,それは知能です.しかし,その方法は人間とはかなり異なっています.例えば,深層学習は,大量のデータに基づき,手書き文字を人間またはそれ以上に正しく認識することができます.人間の場合,恐らく,活字体の学習だけで手書き文字をかなりの確かさで認識できるようになります.学習・記憶法の違いや文脈の利用等が理由だと思います.囲碁や将棋の世界では,プロの方は,対戦経験や過去の棋譜を勉強しながら,その能力を高めているのだと思いますが,人間が行うデータ処理の量には限界があります.従って,人間の能力を遙かに上回る大量の棋譜に基づいて学習したコンピュータは,人間との勝負に勝つ可能性は十分あります.しかし,棋譜に現れていないような状況,例えば,素人と対戦した場合はどうなるのでしょうか.また,将棋のプロの方は,たとえチェスに対する経験が無くても,そのルールを知りさえすれば,すぐにかなりの腕前になれるのではないでしょうか.しかし,コンピュータの場合はどうでしょうか.
- 深層学習は,大量のデータに基づき,その中に含まれるより一般的な知識を獲得し,何らかの処理(分類処理)を行うような分野では,人間またはそれ以上の能力を発揮すると思います.少なくとも今までは,コンピュータが力を発揮したのは演繹推論の世界です.公理,定理,推論過程に誤りが無ければ,基本的に推論結果は正しいはずです.しかし,深層学習は,帰納推論の世界に踏み込んできています.帰納推論の世界においては,推論結果が常に正しいとは限りません.つまり,入力データとプログラムが正しくても,誤った結論を出す可能性があります.それをどのようにして見極めれば良いのでしょうか.対象となる分野の専門家が見ても,「結果がおかしい!」という判断ができない可能性もあります.今までのように,コンピュータの能力を上手に利用していかなければなりませんが,その利用方法に大きな違いが出てくるかもしれません.AI の利用方法について,早急に検討すべき問題だと思います.
- 現時点では,学習したデータの範囲から大きく外れるような状況では何が起こるか予測できません.獲得した一般的な知識を,他の分野に転移させることも不可能です.今後,多くの分野で,コンピュータが人間の知能を上回るような技術が現れてくると思います.しかし,人間と同じような一般的学習(知識の転移などが可能な開かれた学習)能力をコンピュータが獲得できるか否か,もし,獲得できれば,人間以上の知能を持ったコンピュータが出現することになりますが,今の段階では,全く不明な状況です.もし,そのようなコンピュータが出現すれば,どうなるのでしょうか?
- 一般に,x が集合 A の要素であるか否かは一意に決まります.従って,以下に示す E や F は集合とは言えません.
- E = {x | x は袋井に近い市町村}
- F = {x | x は小さい整数}
- しかし,ファジイ集合では,上のようなものを一種の集合として扱うことができます.ファジイ集合においては,ある要素がファジイ集合に含まれるか否かを,含まれる度合いを表すメンバーシップ関数によって決めます.メンバーシップ関数の定義方法に特別な規則があるわけではありません.基本的には,メンバーシップ関数としての性質を備えていさえすれば,どのように定義しても構いません.例えば,上記のファジイ集合 E に対して,以下に示すいずれのメンバーシップ関数を使用しても構いません.一般に,ファジイ集合を使用する目的,計算時間等によって決まってきます.
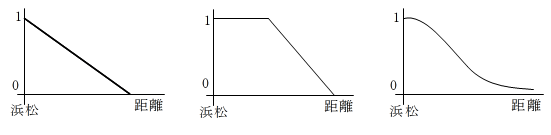
- ファジイ集合が使用される場面として,動的システムの制御が挙げられます.制御規則を複数のファジイ規則によって記述しておき,それらの規則から推論(ファジイ推論)を行い,その結果によって制御対象を制御する方法です.例えば,ファジイ規則,
- R1: if x1 = A11 and x2 = A12 then y = B1
- R2: if x1 = A21 and x2 = A22 then y = B2
- ・・・
- について考えてみます.Aij,Bi はファジイ集合を表し,各規則は,例えば,「温度が低く,圧力が中くらいの時は,電圧を高くせよ」などの規則を表現したものになります.これらの規則から,実際の温度,圧力が与えられたときの電圧を推論し,制御を行うことになります.
- 推論結果は,規則の記述方法,ファジイ集合(メンバーシップ関数)の定義方法,推論方法等によって異なってきますが,非常に乱暴な言い方をすれば,規則に与えられたデータの内挿に相当します.実際,線形内挿と一致するような規則,推論方法を設定することも可能です.変数の数が多くなると,内挿方法自体がかなり面倒になりますが,ファジイ推論においては,変数の数が多くても,すべて同様の手続きで結果を計算することができます.
- 動的システムを対象とした場合,何らかの形で制御が行われるはずです.組み込みシステムによって何かを動かす場合はもちろん,そうでなくても,制御的な考え方は重要だと思います.ここでは,制御理論,特に古典制御理論について簡単に説明します.
- 制御とは
- 一般に,システムの解析・設計に対しては何らかの目的が伴います.例えば,ある部屋の空調システムを設計する場合は,そのシステムによって,部屋の温度などを適切な値に設定できなければ意味がありません.そこで,「制御」という考え方が重要になってきます.一般的に述べれば,
- 「制御とは,システムの出力が目的の状態になるように,システムに操作を加えることである」
- といえます.
- システムを制御するには,大きく分けて二つの方法があります.フィードフォワード制御( Feedforward Control,開ループ制御:Open Loop Control )とフィードバック制御( Feedback Control,閉ループ制御:Closed Loop Control)です.部屋の温度を制御しようとした場合,一日の気温の変化,室内の人数変化,扉の開閉時間・回数などを正確に予測できれば,空調機の運転スケジュールを前もって決めておくことによって部屋の温度を目標とする温度に正確に設定できるはずです.このような制御をフィードフォワード制御と呼び,その概念図は以下のようになります.この図において,制御対象が温度制御をしたい部屋,制御要素が空調機,被制御量が室温に相当します.

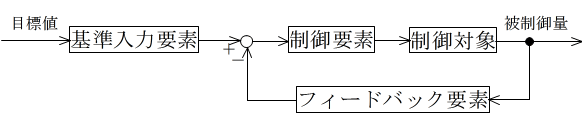
- しかし,この方法では,温度変化や人数変化が予測と異なった場合(システムに外乱が加わった場合)は,目標とする温度を保つことはできません.さらに,設定温度を変更したいような場合は,最初から制御スケジュールを設計し直す必要があります.そこで考えられるのが,現時点における部屋の温度(被制御量)を測定し,その値を制御要素の前まで戻し(フィードバックし),目標値(設定したい室温)と比較し,その差に見合った操作を行ってやる方法です.つまり,室温が目標値より高ければ,空調機に室温を下げるような動作をさせ,逆に低ければ室温を上げるような動作を行わせる方法です.これがフィードバック制御であり,その概念図は以下のようになります.基準入力要素は,目標値を基準入力信号(電流,電圧など,制御要素を操作する信号)に変換する要素,また,フィードバック要素は,被制御量を基準入力信号と比較できる信号に変換する要素です.
- この章では,基本的に,フィードバック制御を扱います.特に,制御というものを概念的に理解してもらうために,制御理論に関する詳細な説明は省略すると共に,制御システムの解析に重点を置き,制御システムをどのようにして設計するかについてはほとんど触れません.
- 制御システムのモデル
- 制御システムを解析・設計するためには,そのモデルが必要になります.「システムのモデルとシミュレーション」の章で述べたように,一般に,物理システムは常微分方程式によって記述可能です.熱の移動に関するシステムのように,偏微分方程式で記述される分布定数系も存在しますが,それらのシステムも,場合によっては,常微分方程式で記述される集中定数系で近似して解析することが可能です.そこで,制御理論においては,主として,常微分方程式で記述されるシステムを対象とします.
- 厳密に言えば,ほとんどの場合,システムは非線形常微分方程式で記述されます.非線形常微分方程式は,その一般解を求めることができないため,解析が非常に困難になります.しかし,興味の対象となる状態の近傍(例えば,部屋の設定温度の近傍)だけを考えれば,定係数線形常微分方程式によって近似することができます.定係数線形常微分方程式の一般解を求めることは可能であり,また,線形システム(線形系)においては,「重ね合わせの理」が成立し,解の導出や解析が容易になります.「重ね合わせの理」とは,システムへの入力が u1 のときその出力が y1,入力が u2 のとき y2 であったとすると,a,b を定数としたとき,(au1 + bu2)の入力に対してその出力は (ay1 + by2)となるような性質です.このため,制御理論においては,多くの理論が定係数線形常微分方程式で記述されるシステムを対象としています.この節においても,1 入力 1 出力の定係数線形常微分方程式で記述されるシステムを対象とします.具体的には,システムへの入力を u(t),出力を y(t) としたとき,次の微分方程式によって記述されるシステムを対象とします.ここで,a0,・・・,an,b0,...,bmは定数とします( n ≧ m ).
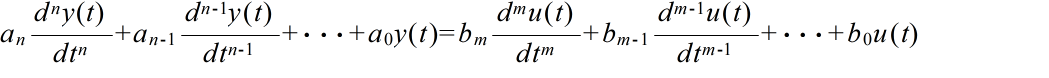
- 線形であるとはいえ,次数が高くなると解を求めることは面倒な仕事になります.そこで微分方程式を直接解くことなく,システムの解析・設計を行う方法として,伝達関数を使った方法がよく使用されます.伝達関数モデルを利用することによって,微分方程式を代数方程式として取り扱うことが可能になり,解析・設計が容易になります.
- 伝達関数は,「すべての初期値を零にしたときの出力信号と入力信号の比」として定義されます.例えば,先に述べた微分方程式で表現されるシステムの伝達関数 G(s) は,両辺を,初期値 = 0 としてラプラス変換(時間領域を周波数領域に変換)することによって,以下のようになります.
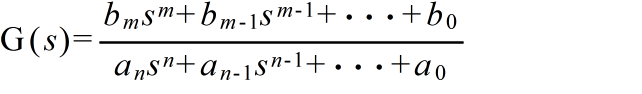
- このとき,伝達関数の分母を零とおいた方程式を特性方程式と呼びます(微分方程式の特性方程式と同じ).また,分子を零とおいた方程式の根を零点,特性方程式の根を極と呼びます.
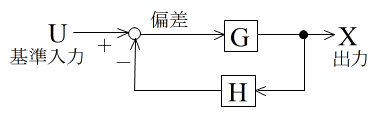
- システムのモデルとして伝達関数が使用されるとき,ブロック線図がしばしば使用されます.ブロック線図は,システム内における信号(情報)の流れを表すものであり,回路図などと似ていますが,回路図とは異なり,信号の流れだけを表現し,エネルギー等の流れを表現していないことに注意してください.例えば,代表的なフィードバック制御システムのブロック線図は上図のようになります.
- 伝達関数モデルでは,1 入力 1 出力システムだけを扱い,また,入力や出力の導関数などを消去しています.しかし,場合によっては,導関数を利用した方がより優れた制御が可能な場合もあります.さらに,一般のシステムにおいては,多入力多出力になり,それらの変数間の相互関係が重要になります.そこで,システムの構造に基づき,その内部状態を使用したシステムの記述が望まれます.それが状態方程式です.
- 一般に,n 次の線形システムの状態方程式は以下のようになります( x の上に書かれた点(「・」)は,時間による微分( d / dt )を表しています).これらの式において,x をシステムの状態変数と呼びます.また,(1) 式を状態方程式,(2) 式を出力方程式と呼ぶ場合もあります.なお,先に述べた微分方程式は,適当な変数変換によって状態方程式の形に変形することができます.その際,特性方程式の根は,行列 A の固有値に一致します.
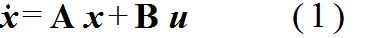
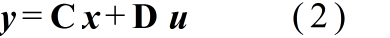
- x: 状態ベクトル( n × 1 )
- u: 入力ベクトル( p × 1 )
- y: 出力ベクトル( m × 1 )
- A,B,C,D: 行列(各々, n × n, n × p, m × n, m × p )
- 制御システムの特性
- 例として,部屋の温度を制御する空調システムについて考えてみます.このシステムの場合,以下に示すようなことが要求されるはずです.この点は,他の動的システムにおいても同様です.
- 1) 十分時間がたてば,被制御量(室温)が目標値(設定温度)に一致する(定常特性)
- 2) できるだけ速く被制御量が目標値に一致する(速応性)
- 3) 時間の経過と共に,定常状態に近づく(安定性)
- システムが以上述べた性質を満足するか否かを見るためには,システムの動特性を知る必要があります.システムの動特性を見る一つの方法は,システムに何らかの入力を加え,その出力を観察することです.制御理論では,入力として単位インパルス関数や単位ステップ関数がよく使用されます.そして,すべての初期値を 0 としたとき,単位インパルス関数に対する出力をインパルス応答,単位ステップ関数に対する出力をインディシャル応答(単位ステップ応答)と呼びます.例えば,インディシャル応答を見るためには,まず,微分方程式を解く必要があります.その際,ラプラス変換と伝達関数を利用して容易に解くことができます.
- また,周波数応答も,システムの動特性を見る重要な手段です.周波数応答とは,様々な周波数の正弦波をシステムに入力し,その出力のゲイン(振幅)及び位相の変化を見る方法です(線形システムの場合は,正弦波入力に対して,出力も正弦波になる).例えば,高い周波数に対してもゲインが変化しなければ,そのシステムが素早い動きに対応可能であることを意味しています.
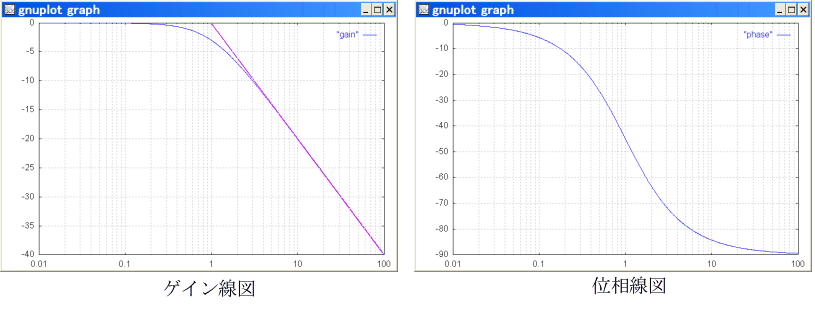
- 周波数応答も,伝達関数から簡単に得られます.システムの伝達関数を G(s) としたとき,横軸に角周波数 ω を対数目盛でとり,縦軸にゲイン |G(jω)| の対数値 20 log10|G(jω)|(単位: デシベル ( dB ) ),及び,位相 ∠G(jω) (単位: 度)をとって表示したグラフをボード線図と呼びます.特に,角周波数とゲインを表示したグラフをゲイン線図,角周波数と位相を表示したグラフを位相線図と呼びます.例えば,G(s) = 1 / (1 + s) ( G(jω) = 1 / (1 + jω) )となるシステムのボード線図は以下のようになります(ピンクの折れ線は近似計算).