- 故障率( Failure Rate )
- 今,
- F(t) = P(X ≦ t) : 時刻 t までに故障する確率(累積故障分布関数,累積故障率)
- R(t) = P(X > t) : t 時間以上故障しない確率(信頼度関数)
- とすると,
- F(t) = 1 - R(t)
- という関係があります.また,
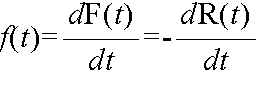
- という関数 f(t) が存在する場合,
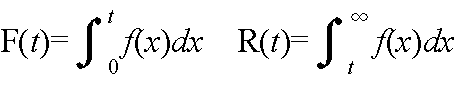
- という関係があります.
- また,単位時間内に故障する割合を λ(t) (故障率,故障率関数,瞬間故障率)とすると,以下に示すような関係があります.
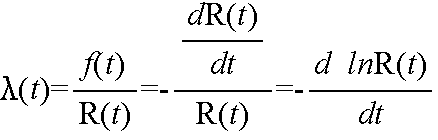
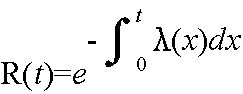
- 故障率は,一般に,以下に示す 3 つの段階を経て変化し,下図のような形をしています.この曲線を,バスタブ曲線と呼びます.
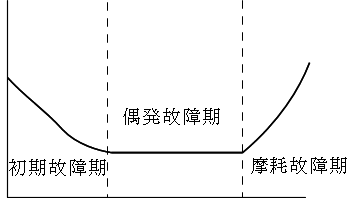
- 初期故障期
- 初期不良が主たる故障の原因となっている期間です.故障率は時間と共に減少します.
- 偶発故障期
- 故障率は一定,つまり,λ(t) = λ となる期間です.従って,故障密度関数は,母数 λ の指数分布をし,信頼度関数は,
- R(t) = e-λt
- となります.
- 故障率は一定,つまり,λ(t) = λ となる期間です.従って,故障密度関数は,母数 λ の指数分布をし,信頼度関数は,
- 摩耗故障期(疲労故障期)
- 故障率は時間と共に増加し,寿命を迎える期間です.この期間の故障密度関数のモデルとしては,ワイブル分布 W(λ, m) がよく使用され,
f(t) = λ m tm-1 e-λ tm F(t) = 1 - e-λ tm R(t) = e-λ tm λ(t) = λ m tm-1
- となります.
- 今,
- 平均故障時間( MTBF: Mean Time between Failures )と平均寿命( MTTF: Mean Time to Failures )
- 故障が発生するまでの動作時間の平均であり,
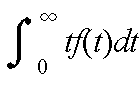
- として定義されます.修理が可能なものに対しては MTBF,修理が不可能なものに対しては MTTF と呼ばれます.故障率が一定値 λ の時は,1 / λ となります.
- 平均故障回復時間(平均修理時間,MTTR: Mean Time to Repair )
- 修理にかかる平均時間です.
- 稼働率( Availability )
- システムがある期間内において運転されている時間の割合であり,以下に示す関係があります.
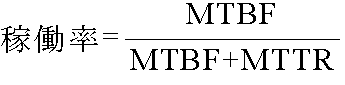
- 保全度( Maintainability )
- 故障が発生してから修理する,または,故障が発生することを防止するために点検,部品の交換を行う保全作業期間の占める割合を言います.
- 耐用寿命( Length of Operating Period )
- システムを使用できる期間のことで,耐用寿命には,装置が摩擦や腐食などにより使用不可能となる寿命のほかに,システムそのものが技術の進歩に取り残されて陳腐化し,装置としては運転可能であっても,性能的にみて著しく時代遅れとなり使用できない場合も含まれます.
- 直列システム

- サブシステムが直列に接続されることによって構成されているシステムです.したがって,システムが正常に動作するためには,各サブシステムがすべて正常に動作している必要があります.
- 例えば,信頼度が Ri(t),故障率が λi(t) であるサブシステムを n 個直列に接続した場合,システムの信頼度,及び,故障率は以下のようになります.
信頼度 R(t) = R1(t)・R2(t)・・・Rn(t) Ri(t) = e-λit の場合: R(t) = e-λ1t・e-λ2t・・・e-λnt 故障率( Ri(t) = e-λit の場合) λ(t) = λ1(t) + λ2(t) + ・・・ + λn(t)
- 並列システム
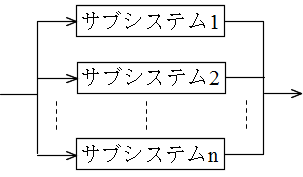
- サブシステムが並列に接続されることによって構成されているシステムです.したがって,システムが正常に動作するためには,各サブシステムのいずれかが正常に動作していれば良いことになります.このようなシステムを冗長システムと呼びます.2 つのシステムに全く同じ処理を同時に実行させ,それらの結果を照合し,結果の正しさを確認しながら処理を進めるデュアルシステムは,その一例です.
- 例えば,信頼度が Ri(t),故障率が λi(t) であるサブシステムを n 個並列に接続した場合,システムの信頼度は以下のようになります.
信頼度 R(t) = 1 - (1 - R1(t))・(1 - R2(t))・・・(1 - Rn(t)) Ri(t) = e-λit であるサブシステムを 2 個接続した場合: R(t) = e-λ1t + e-λ2t - e-(λ1 + λ2)t
- (このように,故障率は直列システムのような簡単な式では表現できません)
- 信頼性向上を目的としたシステム
- 待機システムとは,サブシステムのいくつかを使用せず待機させておき,常時使用しているサブシステムが故障したとき,待機させているサブシステムと切り替えるシステムをいいます.コンピュータシステムにおけるデュプレックスシステムは,その一例です.デュプレックスシステムでは,2 組のシステムを用意し,1 組は稼働状態,他の 1 組は待機状態にしておきます.もし,稼働状態のシステムが故障した場合は,待機状態のシステムを稼働させることになります.待機方法には,ホットスタンバイとコールドスタンバイという 2 つの方式があります.ホットスタンバイ方式は,待機システムにおいても前もって稼働システムと同じプログラムを動作させておき,稼働システムに故障が起こったとき即座に切り替える方式です.また,コールドスタンバイ方式は,稼働システムに故障が起こってから,待機システムに稼働システムが実行していたプログラムを起動して切り替える方式です.
- ここで,待機システムにおける信頼度について考えてみます.例えば,今,2 つのサブシステム A,および,B から成っているシステムがあり,サブシステム A は常時使用し,サブシステム B は,通常は稼働しておらず,A が故障したときに切り替えて使用するものとします.いずれのシステムの故障率も一定値 λ であるとき,システムの信頼度は以下のようにして計算できます.
- 信頼度 = (A が時間 t までに故障しない確率)
- + (時間 t より前の時刻 τ で A が故障し,その後,B が時間 t まで故障しない確率)
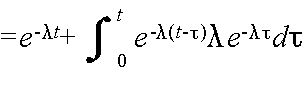
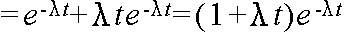
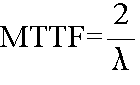
- ただし,一般には,待機システムの信頼度が,待機中に低下することも考慮する必要があります.
- 信頼性を高めるためには,ハード面,及びソフト面の両面にわたった信頼性設計が重要となります.構成部品の信頼度を上げて故障が発生しないようにするという考え方をフォールトアポイダンスといいます.逆に,障害の発生を見越して,例え故障が発生しても,システム全体としての機能を失わないようにする考え方をフォールトトレラントといいます.フォールトトレラントを実現する方法としては以下に示すようなものがあげられます.
- フェイルセーフ: 故障が発生した場合,常に安全な状態に移行するといった考え方(安全性重視)であり,例として,「石油ストーブを倒すと消える」,「信号機が故障したら,信号を赤にする」などがあげられます.
- フェイルソフト: システムの一部に障害が発生した場合,故障した個所を切り離すなどの操作によって,例え機能を低下させてもシステムの稼動を続けるといった考え方(継続性重視)であり,例として,「停電が発生したら,バッテリー電源に切り替える」などがあげられます.
- フールプルーフ: 利用者が操作や手順を間違えても,誤動作が起こらないようにするという考え方であり,例として,「ファイルを削除する場合に,警告メッセージを出す」などがあげられます.
- 待機システムとは,サブシステムのいくつかを使用せず待機させておき,常時使用しているサブシステムが故障したとき,待機させているサブシステムと切り替えるシステムをいいます.コンピュータシステムにおけるデュプレックスシステムは,その一例です.デュプレックスシステムでは,2 組のシステムを用意し,1 組は稼働状態,他の 1 組は待機状態にしておきます.もし,稼働状態のシステムが故障した場合は,待機状態のシステムを稼働させることになります.待機方法には,ホットスタンバイとコールドスタンバイという 2 つの方式があります.ホットスタンバイ方式は,待機システムにおいても前もって稼働システムと同じプログラムを動作させておき,稼働システムに故障が起こったとき即座に切り替える方式です.また,コールドスタンバイ方式は,稼働システムに故障が起こってから,待機システムに稼働システムが実行していたプログラムを起動して切り替える方式です.
