- [定義] 有限個の対象から幾つかを取り出しそれを順に並べたものを順列という.一方,取り出した順序を問題にしないで,それらの組合せだけに注目するとき,その組を組合せという.
- 例 1.1: 例えば,3 個の数字 {1, 2, 3} から,2 個の数字を取り出した順列は,
- (1, 2), (2, 1), (1, 3), (3, 1), (2, 3), (3, 2)
- の 6 種類あります.しかし,組み合わせは,順序を問題にしませんので,
- (1, 2), (1, 3), (2, 3)
- の 3 種類になります.
- [定理 1.1] 相異なる n 個のものから r 個をとる順列の総数は,
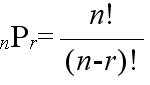
- である.
- [定理 1.2] n 個のものから r 個を取り出す組合せの数は,
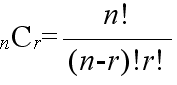
- である.
| n | n2 | n3 | n4 | n5 | n! |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 |
| 5 | 25 | 125 | 625 | 3126 | 120 |
| 10 | 100 | 1000 | 10000 | 100000 | 3628800 |
| 20 | 400 | 8000 | 160000 | 3200000 | 2.43 × 1018 |
| 50 | 2500 | 125000 | 6250000 | 312500000 | 3.04 × 1064 |
- [定理 1.3] n 個の内で,p 個は同じもの,q 個は他の同じもの,・・・,s 個がまた他の同じものであるとき,これらの n 個を並べる順列の数は,
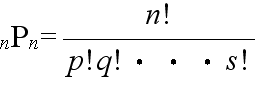
- である.
- [定理 1.4] 相異なる n 個のものを円形に並べる順列(円順列)の数は,
- n-1Pn-1 = (n - 1)!
- である.
- [定理 1.5] n 個のものから重複を許して r 個とる順列(重複順列)の数は,
- nΠr = nr
- である.
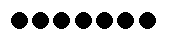
- [定理 1.6] n 個の中から,重複を許して r 個とる組合せの数は,
- nHr = n+r-1Cn-1 = n+r-1Cr
- である( r < n とは限らない)
- [定理 1.7] 組合せの数 nCr に関しては,次の式が成り立つ
- (1) nCr = nCn-r
- (2) nCr = n-1Cr + n-1Cr-1 (パスカルの公式)
- (1) nCr = nCn-r
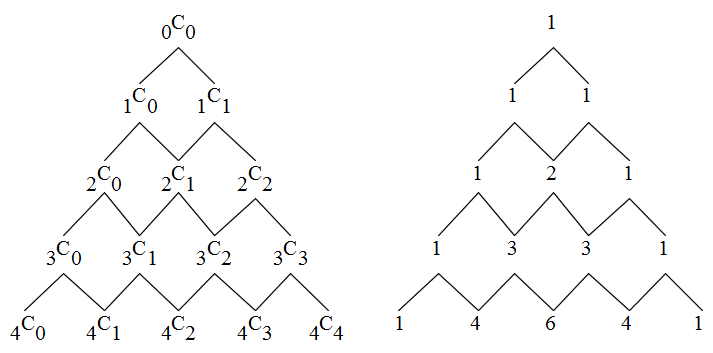
- [定理 1.8] 二項定理
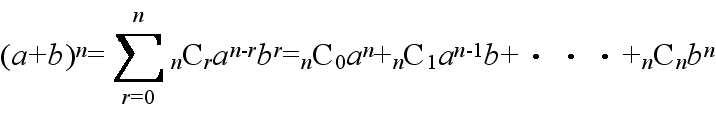
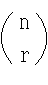
- 例1.2: (x + 2)10における x3の係数
- 10C327 = 120 x 128 = 15360
- [定理 1.9] 多項定理
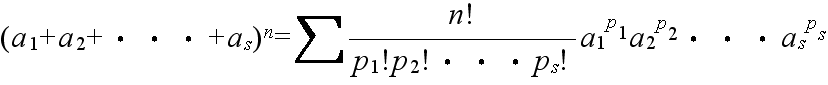
- ただし,p1, p2, ・・・, ps は 0 または正の整数であり,Σ は p1 + p2 + ・・・ + ps = n となるすべての整数値 p1, p2, ・・・, ps についての和を表す.

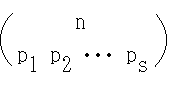
- 例1.3: 女 3 人,男 2 人を 1 列に並べるとき,女が 3 人隣り合うような並べ方は何通りありますか.
- 女 3 人を 1 かたまりとして考える.女のかたまりと男 2 人で順序を考えると,
- 3P3 = 6
- 女 3 人も順序が変わるので,
- 3P3 = 6
- したがって,
- 6×6 = 36
- 例1.4: 男 3 人、女 4 人を 1 列に並べるとき,男どうしが隣り合わない並び方は何通りありますか.
- ○女○女○女○女○
- のように並び,○の中の 3 カ所に男を配置すればよい.まず,女の並び方は
- 4P4 = 24
- 男は,○の中から 3 カ所を選び,その並び方を数えればよいから,
- 5P3 = 60
- 従って,答えは,
- 24 × 60 = 1440
- 例1.5: 0 ~ 9 まで書いたカードが 1 枚ずつあります.このとき,以下の問に答えなさい.
- (1)3 枚取り出して 3 桁の数を作るとき,何通りできますか.
- 最初の数字の選び方×残り2つの数字を選び並べる方法
- 9 × 9P2 = 648 通り
- (2)3 枚取り出して 3 桁の偶数を作るとき,何通りできますか.
- 1の位が 0 のとき: 9P2 = 72
- 1の位が 2,4,6,8 のとき:各々,0 以外からの最初の数字の選び方 * 残りのカードから 2 番目の数字の選び方 = 8 * 8 = 64
- よって,72 + 64 * 4 = 328 通り
- 例1.6: 男 4 人,女 2 人がいるとき,以下の問に答えなさい.
- (1)両端に女が座るように横 1 列に並ぶ座り方は何通りありますか.
- 女 2 人の座り方:2, 残り 4 人の座り方:4P4 = 24, 従って 2 * 24 = 48 通り
- (2)両端に男子が座るように横 1 列に並ぶ座り方は何通りありますか.
- 両端の男 2 人の座り方:4P2 = 12, 残り 4 人の座り方:4P4 = 24, 従って 12 * 24 = 288 通り
- (3)6 人が円卓に着く場合,座席の座り方は何通りありますか.
- 円順列であるので,6-1P6-1 = 120 通り
- (4)6 人が円卓に着く場合,円卓上で女 2 人が隣合わないような座席の座り方は何通りありますか.
- 女が隣り合う場合を考える(この値を全体の数から引く)
- 女 2 人の座り方:2, 女 2 人を 1 人と考えた 5 人の座り方:4P4 = 24
- 従って 120 - 2 * 24 = 72 通り
- 例1.7: 袋の中にある色の違う 8 つの玉から 2 つだけ取り出す方法は,何通りありますか.
- 8C2 = 8・7 / 2・1 = 28
- 例1.8: 青い玉が 6 個,透明の玉が 2 個,赤い玉が 1 個あります.これらを 1 列に並べるとき,何通りの組み合わせができますか.
- 9 カ所から 6 カ所の選び方 * 3 カ所から 2 カ所の選び方 = 9C3 * 3C2 = 84 * 3 = 252 通り
- 例1.9: 5 円,10 円,50 円,及び,100 円の 4 種類の硬貨が 2 枚ずつあるとき,以下の問に答えなさい.
- (1)この硬貨を 2 枚使ってできる異なる金額になる組み合わせは何通りですか.
- 異なる硬貨を 2 枚選ぶ方法 4C2 = 6 通り
- 同じ硬貨を 2 枚選ぶ方法 4 通り
- よって,6 + 4 = 10 通り
- (2)種類の異なる硬貨 3 枚使ってできる金額は何通りありますか.
- 異なる硬貨を3枚選ぶ方法 4C3 = 4 通り
- 例1.10: 下図のような碁盤の目に整備された道路があるとき,以下の問に答えなさい.
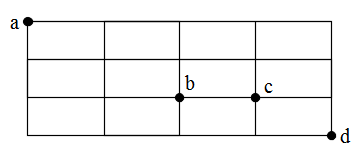
- (1)b 点を通って a 点から d 点に行く方法は何通りですか.
- a から b へ行くには,2 個の縦,及び,2 個の横を通る必要があるので,4 個の路から 2 個の水平経路を選ぶ方法に相当する
- a から b へ行く方法: 4C2 = 6
- 同様に
- b から d へ行く方法: 3C2 = 3
- 従って,b を通って a から d へ行く方法: 6 * 3 = 18 通り
- (2)c 点を通らずに a 点から d 点に行く方法は何通りですか.
- a から c へ行くには,2 個の縦,及び,3 個の横を通る必要があるので,5 個の路から 3 個の水平経路を選ぶ方法に相当する
- a から c へ行く方法: 5C3 = 10
- 同様に
- c から d へ行く方法: 2C1 = 2
- 以上より,c を通って a から d へ行く方法: 10 * 2 = 20 通り
- 制限をつけずに a から d へ行く方法は,7C4 = 35 通り
- 従って,c を通らずに a から d へ行く方法: 35 - 20 = 15 通り
- 例1.11: 男 4 人と女 3 人の計 7 人のグループから 2 人の代表を選びたいとします.このとき,男が少なくとも 1 人は含まれるように選ぶとすると,選び方は何通りありますか.
- 全体か 2 人選択 - 女子から 2 人選択 = 7C2 - 3C2 = 21 - 3 = 18 通り
- [定義] 一定の条件の下で繰り返し行うことができ,その結果が偶然に支配されるような実験や観測を一般に試行という.試行によって起こる可能性のあるすべての事柄の集合 Ω が確定しているとき,その集合を考えている試行の標本空間といい,その要素を標本点,または,単に標本空間の点という.
- [定義] 標本空間 Ω の部分集合を事象といい,試行の結果が 1 つの事象 A に属するとき,事象 A が起こったという.標本点の 1 つ 1 つを特に根元事象という.それに対して,2 個以上の点からなる事象を複合事象という.また,標本空間全体を全事象,決して起こらない事柄は φ で表され,それを空事象という.
- 例 2.1: 1 つのさいころを,1 回だけ投げることについて考えてみます.明らかに,この結果は偶然性に左右され,試行と考えることができます.このとき,標本空間 Ω は,「 k の目が出る」ことを k で表すと,
- Ω = { 1, 2, 3, 4, 5, 6 }
- となります.根元事象は,1, 2, 3, 4, 5, 及び, 6 であり,また,複合事象としては,いろいろ考えられますが,「偶数の目が出る事象 A 」という場合であれば,以下のようになります.
- 偶の目が出る事象 A = { 2, 4, 6 }
- [定義] 以下の定義において,例 2.1 を具体的な例として説明を行う.
- (1) 和事象 A ∪ B : 事象 A または B が起こるという事象.例えば,事象 A を「 4 以下の目が出る」,また,事象 B を「偶数の目が出る」事象としたとき,事象「 A ∪ B 」は,{ 1, 2, 3, 4, 6 } となる.
- (2) 積事象 A ∩ B : 事象 A と B が同時に起こるという事象.例えば,事象 A を「 4 以下の目が出る」,また,事象 B を「偶数の目が出る」事象としたとき,事象「 A ∩ B 」は,{ 2, 4 } となる.
- (3) 余事象 A : 標本空間 Ω の中で,事象 A が起こらないという事象.例えば,事象 A を「 4 以下の目が出る」事象としたとき,余事象は,{ 5, 6 } となる.
- (4) 排反事象 事象 A と B が同時に起こることがない時,記号的には A ∩ B = φ である時,事象 A と B は互いに排反である,または,排反事象であるという.例えば,事象 A を「奇数の目が出る」,また,事象 B を「偶数の目が出る」事象としたとき,これらの事象は排反である.
- (1) 和事象 A ∪ B : 事象 A または B が起こるという事象.例えば,事象 A を「 4 以下の目が出る」,また,事象 B を「偶数の目が出る」事象としたとき,事象「 A ∪ B 」は,{ 1, 2, 3, 4, 6 } となる.
- [定義] 有限な標本空間Ωにおいて,どの根元事象も同程度に確からしく起こるものとする.標本空間 Ω の中のある事象 A に対して,n(A),n(Ω) を標本空間 Ω 及び事象 A に含まれる根元事象の数としたとき,
- P(A) = n(A) / n(Ω)
- を事象 A の数学的確率(確率)という.
- 例2.2: 例2.1 において,各目が同程度に確からしく起こるとすれば,各目が出る事象に 1/6 という数値を対応させると,上の定義から,明らかにこれは確率となります.
- [大数の法則] ある試行を N 回繰り返し行い,事象Aが起こった回数が n 回であるとき,n / N を相対度数という.試行回数 N を十分大きくするとき相対度数 n / N が,ほぼ一定値 p に近づくならば,p を事象Aの起こる統計的確率(経験的確率)という.このように定義された p が,試行回数 N を大きくしていくと,事象Aの本来持っている確率(先験的確率)に限りなく近づくことが知られており,これを大数の法則という.
- [定義] 標本空間 Ω の各事象 A に対して次の 3 つの条件を満たす実数 P(A) が対応させられるとき,その値 P(A) を事象 A の起こる確率という.各事象に対して確率が与えられる標本空間を確率空間といい,各事象を確率事象という.
- (1) 任意の事象 A に対して,0 ≦ P(A) ≦ 1
- (2) P(Ω) = 1, P(φ) = 0
- (3) 事象 A と B が互いに排反,即ち A ∩ B = φ ならば,以下の関係が成立する.
- P(A ∪ B) = P(A) + P(B)
- (1) 任意の事象 A に対して,0 ≦ P(A) ≦ 1
| 根元事象 | E1 | E2 | ・・・・・ | EN | 全事象Ω |
|---|---|---|---|---|---|
| 確率 | p1 | p2 | ・・・・・ | pN | 1.0 |
- [定理 2.1]
- (1) 事象 A1,A2,・・・,Ar が排反ならば
- P(A1 ∪ A2 ∪・・・∪ Ar) = P(A1) + P(A2) + ・・・ + P(Ar)
- (2) 任意の 2 つの事象 A,B に対して
- P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
- (3) 余事象に対して
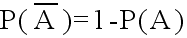
- (4) A ⊂ B ならば,P(A) ≦ P(B)
- (1) 事象 A1,A2,・・・,Ar が排反ならば
- [定義] P(A) > 0 であるとき,事象 B に対して,
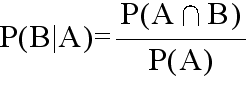
- と定義し,事象 A が起こったときの事象 B の条件付確率という.
- [定理2.2](乗法法則) P(A) > 0,P(B) > 0 であるとき,以下の式が成立する.
- P(A ∩ B) = P(A)P(B | A) = P(B)P(A | B)
- [定理 2.3] ベイズの定理 事象 A1,A2,・・・,Ar が互いに排反であり,かつ,その内どれかの事象が必ず起こるとき,即ち,
- Ai ∩ Aj = φ ( i ≠ j )
- A1 ∪ A2 ∪・・・∪ Ar = Ω
- A1 ∪ A2 ∪・・・∪ Ar = Ω
- ならば,任意の事象 B に対して次の式が成り立つ.
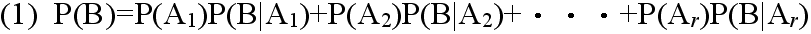
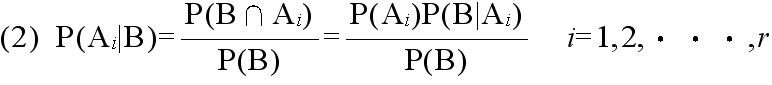
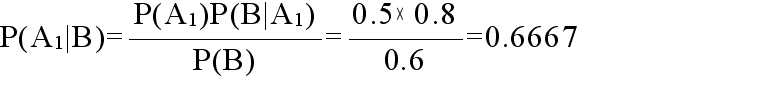
- 例 2.3: 患者がある種の症状(例えば,咳が出るなど)を訴えるとき,その 5 %が A 疾患であることが知られているとします.また,ある精密検査 B は,真の A 疾患患者に対して 70 %陽性反応を示し,疾患でない患者に対しても 10 %陽性反応を示すものとします.先の症状を訴えた患者の精密検査結果が陽性反応を示したとき,その患者が A 疾患である確率はどのようになるでしょうか.
- 事象を
- 事象を
- A1 : A 疾患である
- A2 : A 疾患でない
- A2 : A 疾患でない
- とすると,ベイズの定理は満たされています.また,事象 B を,
- B : 精密検査 B が陽性である
- とすると,以下の確率が得られます.
- P(A1) = 0.05 A 疾患である確率(事前確率)
- P(B | A1) = 0.7 A 疾患である場合に,精密検査結果が陽性になる確率
- P(B) = 0.05 × 0.7 + 0.95 × 0.1 = 0.13 精密検査結果が陽性になる確率
- P(B | A1) = 0.7 A 疾患である場合に,精密検査結果が陽性になる確率
- 以上の点から,精密検査結果が養成であった場合における A 疾患である確率(事後確率)は,ベイスの定理から以下のようになります.
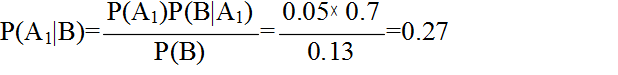
- [定義] r 個の事象 A1,A2,・・・,Ar に対し,それらの任意個の異なる事象の組合せ Ai,Aj,・・・,Ak に対して
- P(Ai ∩ Aj ∩・・・∩ Ak) = P(Ai) P(Aj) ・・・ P(Ak)
- が成り立つとき,事象 A1,A2,・・・,Ar は互いに独立(統計的に独立)であるという.また,1 回毎の試行がそれ以外の試行に何らの影響を及ぼさないとき,すなわち各回の試行が互いに独立であるとき,このような試行を独立試行,または,ベルヌーイ試行という.
- 例2.4: 1 から 10 までの数字が書かれたカードがあり,佐藤さんは 2 から 10 までの偶数が書かれたカードを持ち,鈴木さんは 1 から 9 までの奇数の数字が書かれたカードを持っています.2 人が 1 枚カードを出して数の大きさを比べるとき,佐藤さんのほうが大きい数になる確率はいくらですか.
- 起こりうるすべての場合:5 * 5 = 25 通り
- 佐藤さんの方が大きくなる組み合わせ
- (2, 1) 1通り
- (4, 1), (4, 3) 2通り
- (6, 5), (6, 3), (6, 1) 3通り
- (8, 7), (8, 5), (8, 3), (8, 1) 4通り
- (10, 9), (10, 7), (10, 5), (10, 3), (10, 1) 5通り
- 例2.5: ある人が 2 問からなるテストを受けました.このテストにおいて,第 1 問を正解する確率は 0.7,第 2 問を正解する確率は 0.8 とします.
- (1)2 問とも正解できない確率はいくつですか.
- (1)2 問とも正解できない確率はいくつですか.
- 第 1 問が不正解の確率( 0.3 )× 第 2 問が不正解の確率( 0.2 ) = 0.06
- (2)2 問のうち,1 問だけ正解する確率はいくつですか.
- 1 問正解する確率は,「第 1 問を正解」して「第 2 問を不正解」,または,「第 1 問が不正解」で「第 2 問は正解」の 2 つに分かれます.従って,(0.7×0.2=0.14)+(0.3×0.8=0.24) = 0.38
- または,余事象の考え方を使って,全体から,「両方とも正解する確率」と「両方とも不正解の確率」を引くことによっても得られます.従って,1 - 両方とも正解の確率(0.7×0.8 = 0.56)- 両方とも不正解の確率(0.06)
- 例2.6: 百円硬貨を 4 枚同時に投げたとき,1 枚が表,3 枚が裏となる確率はいくつになりますか.
- 全体の起こり方:2 個(表と裏)の中から,重複を許して 4 個を取り出す順列 = 2Π4 = 24 = 16 通り
- 表が 1 枚,裏が 3 枚出る場合(4 個のうちいずれかが表になる場合) = 4 通り
- 例2.7: ジョーカーを除く 52 枚のトランプから 3 枚抜き出すとき,3 枚とも違う種類(マーク)になる確率はどうなりますか.
- 52 枚から 3 枚を選ぶ方法 = 52C3 = 22100
- 3 種類選び,各種類から 1 枚選ぶ方法 = 4C3×133 = 8788
- よって,8788 / 22100 = 169 / 425
- 例2.8: 袋の中に赤玉が 5 個,青玉が 4 個,白玉が 3 個入っています.この袋から同時に 2 個の玉を取り出すとします.
- (1)2 個とも青玉が出る確率はいくらですか.
- 12 個から 2 個の取り出し方 = 12C2 = 66
- 青玉から 2 個の取り出し方 = 4C2 = 6
- ∴ 6 / 66 = 1 / 11
- (2)青玉と白玉が 1 個ずつ出る確率はいくらですか.
- 青玉から 1 個,白玉から 1 個の取り出し方 = 4C1 * 3C1 = 12
- ∴ 12 / 66 = 2 / 11
- (3)赤玉が 1 個も出ない確率はいくらですか.
- 赤玉以外から 2 個の取り出し方 = 7C2 = 21
- ∴ 21 / 66 = 7 / 22
- (4)赤玉が少なくとも 1 個出る確率はいくらですか.
- 赤玉以外から 2 個の取り出し方: 7C2 = 21 ∴ 21 / 66 = 7 / 22
- 余事象の考え方を使って,赤玉が少なくとも 1 個出る確率 = 1 - 7 / 22 = 15 / 22
- [定義] 標本空間 Ω で,ある属性について標本がとる可能性がある異なる数値が
- x1,x2,・・・,xk
- であるとする.各標本に対してそれのとる値を対応させる変数 X を考える.Ω 上で X がそれぞれの値をとる確率が定まっているとき,X を確率変数(random variable,stochastic variable)(離散型確率変数)といい,x1,x2,・・・,xk を X の標識という.
- 確率変数 X が値 xi をとるという事象を
- 確率変数 X が値 xi をとるという事象を
- { X = xi }
- で表し,その確率を
- P(X = xi) = pi (i = 1, 2, ・・・, k)
- で示す.このように,X がとる値それぞれに対して確率が定まるため,確率は関数の形で,
- f(x) = pi ( x = xi のとき)
- = 0 (その他の x )
- のように記述できる.この関数を確率変数 X の確率密度関数(probability density function)といい(離散的な場合は,単に,確率関数ということもある),確率変数 X は,確率分布 f(x) に従うという.
- [定義] 確率変数 X がある値 x に対して,X ≦ x である確率 P(X ≦ x ) を,確率変数 X の確率分布関数(distribution function),または,累積分布関数(cumulative distribution function)という.これを F(x) とすれば,次のようにかける.
- F(x) = P(X ≦ x)
- [定理 3.1] 確率分布関数の性質
- (1) P(a < x ≦ b) = P(x ≦ b) - P(x ≦ a) = F(b) - F(a)
- (2) x の非減少関数
- (3) 右連続性 limx→a+0F(x) = F(a)
- (4) F(∞) = 1
- (5) F(-∞) = 0
- (6) 0 ≦ F(x) ≦ 1
- (1) P(a < x ≦ b) = P(x ≦ b) - P(x ≦ a) = F(b) - F(a)
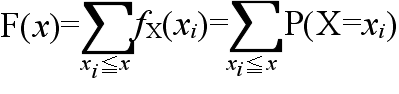
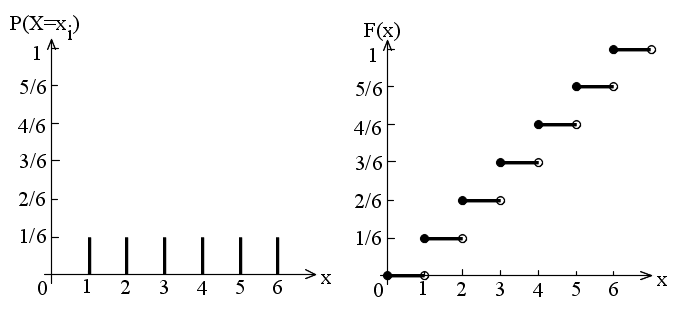
- [定義] 次の式で表される f(x) が存在するとき,f(x) を確率変数 X の確率密度関数という.
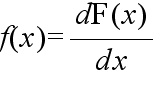
- また,確率分布関数 F(x) は f(x) から
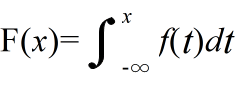
- として与えられる.
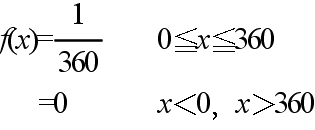
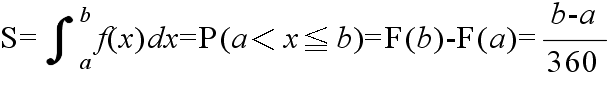
- [定義] 平均(集合平均,期待値)
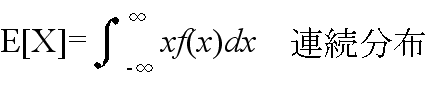
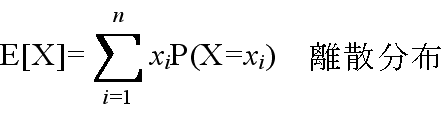
- 例 3.1: さいころの目を確率変数とした X の平均
- E[X] = 1 * 1 / 6 + 2 * 1 / 6 + 3 * 1 / 6 + 4 * 1 / 6 + 5 * 1 / 6 + 6 * 1 / 6
- = (1 + 2 + 3 + 4 + 5 + 6) / 6 = 3.5
- 例 3.2: 1万本のくじに対して下の表の 2 列目,3 列目のような賞金がついている福引きがあるとする.賞金を X 円とすると,下の表の 4 列目に示す確率分布に従う確率変数と考えられる.今1枚の抽選券を持っているとき,いくらの賞金が当たることを期待できるであろうか.
賞金 本数 確率 1 等 10 万円 1 本 1 / 10000 2 等 2 万円 2 本 2 / 10000 3 等 1 万円 10 本 10 / 10000 4 等 千円 200 本 200 / 10000 空くじ 0 円 9787 本 9787 / 10000 - E[X] = 100000 × 1 / 10000 + 20000 × 2 / 10000 + 10000 × 10 / 10000 + 1000 × 200 / 10000 + 0 × 9787 / 10000 = 44 円
- [定義] 分散と標準偏差
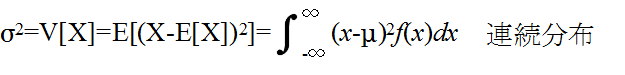

- σ2 を分散,σ を標準偏差と呼ぶ.
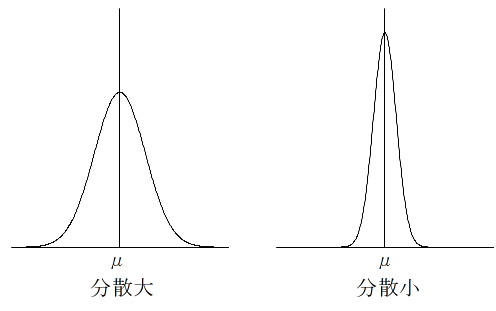
- [定理 3.2](チェビシェフの不等式) 確率変数 X の平均が μ,標準偏差が σ であるとき,次の不等式が成立する.
- P(|X - μ| ≧ kσ) ≦ 1 / k2
- 例 3.3: 学生 200 人に対して試験を行った結果,平均点が 50 点,標準偏差が 5 点でした.35 点~ 65 点の範囲に何人以上の学生がいますか.
- チェビシェフ不等式より,
- P(|X - μ| ≦ kσ)
- = 1 - P(|X - μ| ≧ kσ)
- ≧ 1 - 1 / k2
- = 1 - 1 / 9
- = 8 / 9
- となる.従って,全体の 8 / 9 以上の学生が 35 点~ 65 点の範囲にいることになる.つまり,200 * 8 / 9 = 178 人以上の学生が該当する.
- [定理 3.3] 平均と分散の性質
- (1) a, b を定数として,E[aX+b] = aE[X] + b
- (2) E[X+Y] = E[X] + E[Y]
- (3) X, Y が互いに独立ならば, E[XY] = E[X]E[Y]
- (4) V[X] = E[X2] - E[X]2
- (5) V[aX+b] = a2V[X]
- (6) X と Y が独立ならば, V[X+Y] = V[X] + V[Y]
- (1) a, b を定数として,E[aX+b] = aE[X] + b
- [定義] φ(X) を確率変数 X の関数としたとき,
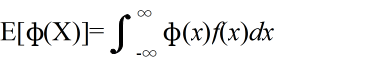
- を φ(X) の期待値という.
- [定義] φ(X) = Xk,または,φ(X) = (X - μ)k ( k = 0, 1, 2, ・・・)としたとき,
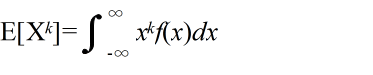
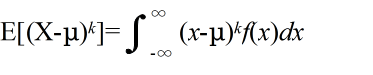
- を,各々,X の原点周りの k 次モーメント( moment ),及び,平均 μ 周りの k 次モーメント( moment )という.
- [定義] φ(X) = eθX としたとき,
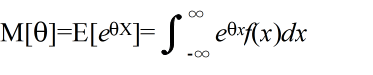
- をモーメント母関数( moment generation function )という.
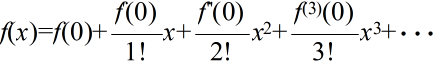
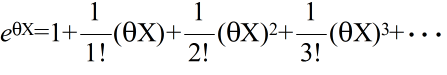
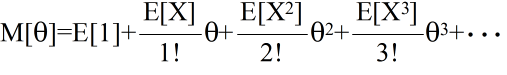
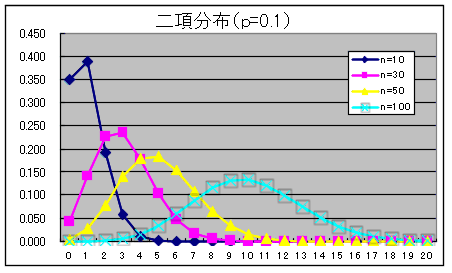
- 二項分布
二項分布の確率密度関数
- C/C++ による密度関数,分布関数を計算するためのプログラム例 →
 (グラフも表示)
(グラフも表示)
- JavaScript 版では,同様の処理を画面上で実行することが可能であり,結果はテキストエリアに出力されると共に,「確率(複数点)」を選択すればグラフも表示されます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「二項分布」をご覧ください.
- 繰り返し行われる独立試行で,もし各々の試みに対して単に 2 つの結果だけが可能で,それらが起こる確率が各試行を通じて一定である場合,その試行をベルヌーイ試行といいます.成功の確率が p で失敗の確率が q = 1 - p であるベルヌーイ試行を n 回行った結果,x 回成功する確率(確率密度関数)は以下のようになり,この分布を母数 p の二項分布と呼びます.
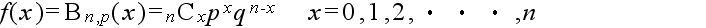
- 二項分布という名称は,この式が,(py + q)n を展開したときの yx の係数に等しいことに由来します.なお,二項分布の確率分布関数,平均,及び,分散は以下のようになります.
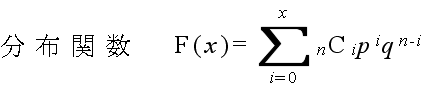
- 平均: E[X] = np, 分散: V[X] = npq
- 二項分布は,n の値が大きくなる( np ≧ 5 と nq ≧ 5 が成立する程度)と後に述べる正規分布,

- に近づきます.
- ポアソン分布
ポアソン分布の確率密度関数

- C/C++ による密度関数,分布関数を計算するためのプログラム例 →
 (グラフも表示)
(グラフも表示)
- JavaScript 版では,同様の処理を画面上で実行することが可能であり,結果はテキストエリアに出力されると共に,「確率(複数点)」を選択すればグラフも表示されます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「ポアソン分布」をご覧ください.
- 二項分布は,p の値が小さく,n の値が非常に大きくなると,λ = np のポアソン分布に近づきます.単位時間内に到着する電話の呼び数 x の分布等がポアソン分布に従うことが良く知られています.母数 λ のポアソン分布の確率密度関数,平均,及び,分散は以下のようになります.
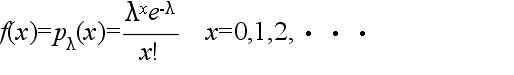
- 平均: E[X] = λ, 分散: V[X] = λ
- ポアソン分布は,λ の値が大きくなる( λ > 10 程度)と,正規分布,

- に近づきます.
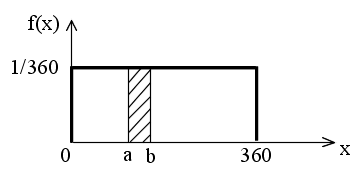
- 一様分布
- C/C++ による密度関数,分布関数,片側α値(片側 p %値)を計算するためのプログラム例 →
 (グラフも表示)
(グラフも表示)
- JavaScript 版では,同様の処理を画面上で実行することが可能であり,結果はテキストエリアに出力されると共に,「確率(複数点)」を選択すればグラフも表示されます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「一様分布」をご覧ください.
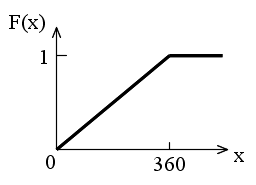
- 先に述べた棒の例が一様分布の例です.一様分布の確率密度関数,平均,及び,分散は以下のようになります.
- 密度関数 f(x) = 1 / (b - a) a ≦ x ≦ b
- = 0 x < a,または,x > b
- 平均: E[X] = (a + b) / 2, 分散: V[X] = (a - b)2 / 12
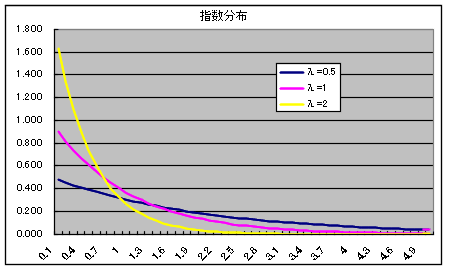
- 指数分布
指数分布の確率密度関数
- C/C++ による密度関数,分布関数,片側α値(片側 p %値)を計算するためのプログラム例 →
 (グラフも表示)
(グラフも表示)
- JavaScript 版では,同様の処理を画面上で実行することが可能であり,結果はテキストエリアに出力されると共に,「確率(複数点)」を選択すればグラフも表示されます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「指数分布」をご覧ください.
- 指数分布は,ポアソン分布と強い関係があります.例えば,電話の呼び間隔が平均 1 / λ の指数分布をするとき,単位時間内に到着する電話の呼び数の分布は平均 λ のポアソン分布をします.母数 λ の指数分布の確率分布関数,確率密度関数,平均,及び,分散は以下のようになります.
- 分布関数 F(x) = 1 - e-λx x ≧ 0
- = 0 x < 0
- 密度関数 f(x) = λe-λx x ≧ 0
- = 0 x < 0
- 平均: E[X] = 1 / λ, 分散: V[X] = 1 / λ2
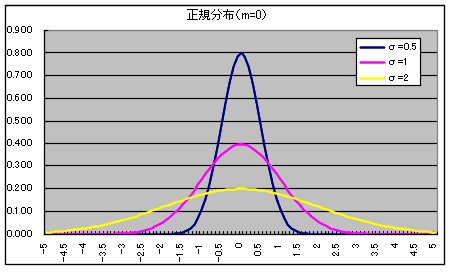
- 正規分布(ガウス分布) N(μ, σ2)
正規分布の確率密度関数
- C/C++ による密度関数,分布関数,片側α値(片側 p %値)を計算するためのプログラム例 →
 (グラフも表示)
(グラフも表示)
- JavaScript 版では,同様の処理を画面上で実行することが可能であり,結果はテキストエリアに出力されると共に,「確率(複数点)」を選択すればグラフも表示されます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「正規分布」をご覧ください.
- 正規分布は,非常によく使われる分布です.母数 μ,σ の正規分布 N(μ, σ2) の確率密度関数,平均,及び,分散は以下のようになります.
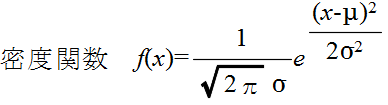
- 平均: E[X] = μ, 分散: V[X] = σ2
- 平均が 0,標準偏差が 1 である正規分布 N(0, 12) を標準正規分布と呼びます.確率変数 X の分布が N(μ, σ2) の正規分布に従うとき,次の変数変換(標準化変換)によって得られる確率変数 Z は標準正規分布 N(0, 12) に従います.
- Z = (X - μ) / σ
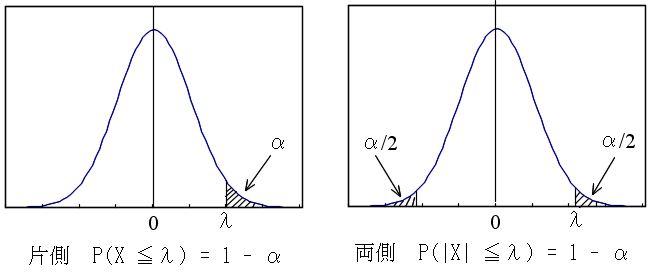
- また,値 α( 0 ≦ α ≦ 1 )に対して,以下の図に示すような値 λ を正規分布の α 値,または,p %値( p = α×100 )といいます.α(斜線部の面積)は,図からも明らかなように,確率変数の値が λ 以上になる確率(両側の場合は,確率変数の値が λ 以上,又は,ーλ以下になる確率)に相当します.α 値は,後に述べる推定において非常に重要となりますので十分理解しておいてください.一般的には,α の値から,λ を求める必要が出てきます.なお,正規分布以外の分布に対しても,同様に,α 値を定義することができます.
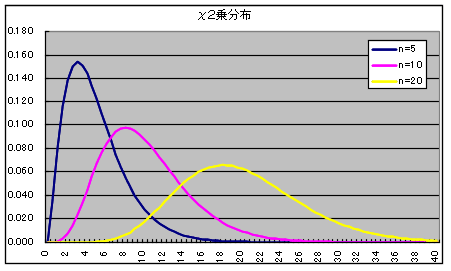
- 自由度 n の χ2 分布
自由度 n の χ2 分布の確率密度関数
- C/C++ による密度関数,分布関数,片側α値(片側 p %値)を計算するためのプログラム例 →
 (グラフも表示)
(グラフも表示)
- JavaScript 版では,同様の処理を画面上で実行することが可能であり,結果はテキストエリアに出力されると共に,「確率(複数点)」を選択すればグラフも表示されます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「χ2 分布」をご覧ください.
- x1,x2,・・・,xn が互いに独立な確率変数で,それぞれが標準正規分布 N(0, 12) に従うとき,
- χ2 = x12 + x22 + ・・・ + xn2
- なる確率変数 χ2 が従う分布を自由度 n の χ2 分布といいます.自由度 n の χ2 分布の確率密度関数,平均,及び,分散は以下のようになります.
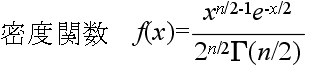
- 平均: E[X] = n, 分散: V[X] = 2n
- ここで,Γ は,ガンマ関数であり,次のように定義されます.
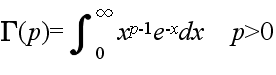
- Γ(1) = 1, Γ(p+1) = pΓ(p)
- Γ(n+1) = n! n: 整数
- C/C++ によるガンマ関数の計算をするためのプログラム例 →

- JavaScript 版では,任意のデータに対するガンマ関数の値を計算することができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「ガンマ関数」をご覧ください.
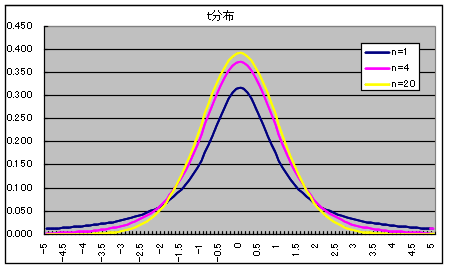
- 自由度 n の t 分布
自由度 n の t 分布の確率密度関数
- C/C++ による密度関数,分布関数,片側α値(片側 p %値)を計算するためのプログラム例 →
 (グラフも表示)
(グラフも表示)
- JavaScript 版では,同様の処理を画面上で実行することが可能であり,結果はテキストエリアに出力されると共に,「確率(複数点)」を選択すればグラフも表示されます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「 t 分布」をご覧ください.
- x1,x2,・・・,xn が互いに独立な確率変数で,それぞれが標準正規分布 N(0, 12) に従うとき,
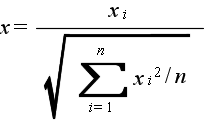
- なる確率変数 x が従う分布を自由度 n の t 分布といいます.自由度 n の t 分布の確率密度関数,平均,及び,分散は以下のようになります.
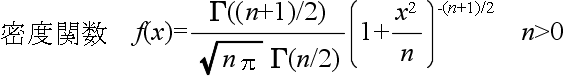
- 平均: E[X] = 0, 分散: V[X] = n / (n - 2)
- 平均,分散は,n ≧ 3
- なお,自由度が大きくなると,t 分布は正規分布に近づき,自由度が無限大になると,標準正規分布 N(0, 12) と一致します.
- 自由度 n1,n2 の F 分布
自由度 n1,n2 の F 分布の確率密度関数
- C/C++ による密度関数,分布関数,片側α値(片側 p %値)を計算するためのプログラム例 →
 (グラフも表示)
(グラフも表示)
- JavaScript 版では,同様の処理を画面上で実行することが可能であり,結果はテキストエリアに出力されると共に,「確率(複数点)」を選択すればグラフも表示されます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「 F 分布」をご覧ください.
- χ12 が自由度 n1 の χ2 分布,χ22 が自由度 n2 の χ2 分布に従い,かつ,χ12 及び χ22が互いに独立であるとき,
- x = (χ12 / n1) / (χ22 / n2)
- なる確率変数 x が従う分布を自由度 (n1, n2) の F 分布といいます.自由度 (n1, n2) の F 分布の確率密度関数,平均,及び,分散は以下のようになります.ただし,平均に対しては n2 > 2,分散に対しては n2 > 4 とします.
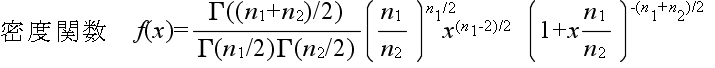

- 同時確率分布
- 例えば,2 個のサイコロを振る場合,それぞれのサイコロの目を X 及び Y として,X = 1,Y = 5 となるような確率を考えるように,同時に 2 つの試行を行ったときの確率分布を調べたい場合があります.このような確率分布を 2 次元確率分布といいます.これに対して,今まで取り扱ってきた 1 変数の場合を 1 次元確率分布といいます,2 次元確率分布に対しても,1 次元確率分布の場合と同様に確率密度関数を定義できます.
- [定義] X のとる値を x1, x2, ・・・, xm,Y のとる値を y1, y2, ・・・, yn とする.また,X が xi( i = 1, 2, ・・・, m ),かつ,Y が yj( j = 1, 2, ・・・, n )の値をとるときの確率が pij,つまり,
- P(X = xi, Y = yj) = pij
- であるとき,
- h(x, y) = pij (xi,かつ,yj のとき)
- = 0 (その他)
- を確率変数 X,Y の同時確率密度関数( simultaneous probability density function )という.
- また,連続型分布に関しては,
- また,連続型分布に関しては,
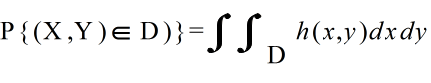
- となるような関数 h(x, y) が存在するとき,h(x, y) 確率変数 X,Y の同時確率密度関数( simultaneous probability density function )という.
- 例 3.4: 10 円硬貨,100 円硬貨を投げて両者の表裏を調べる場合について考えてみます.表に 0,裏に 1 を対応させ,10 円硬貨の表裏を確率変数 X,100 円硬貨の表裏を確率変数 Y とすると,
- h(x, y) = 1 / 4 ( (0, 0), (0, 1), (1, 0), (1, 1) のとき)
- = 0 (その他)
- は,同時確率密度関数となります.
- 2 次元確率分布において,Y の値にかかわらず X の分布を知りたいようなときがあります.このような場合は,それぞれの X における Y の値をすべて足し合わせれば(積分すれば)よいことになります.このことを示すのが次の定義です.
- [定義] 確率変数 X,Y の同時確率密度関数が h(x, y) であるとき,
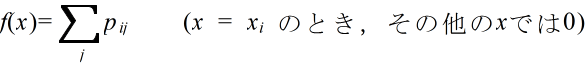
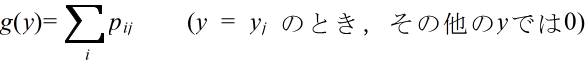
- をそれぞれ h(x, y) より定まる X,Y の周辺確率密度関数( marginal probability density function )という.連続型分布の場合も,同様に,
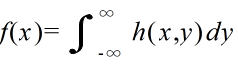
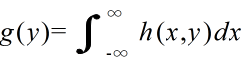
- をそれぞれ h(x, y) より定まる X,Y の周辺確率密度関数( marginal probability density function )という.
- 1 変数の場合と同様,確率変数 X と Y の関数 φ(X, Y) に対して,その期待値を定義できます.
- [定義] φ(X,Y) を確率変数 X,Y の関数としたとき,
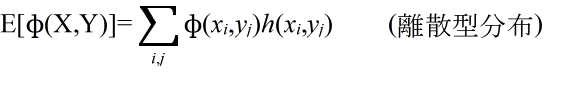
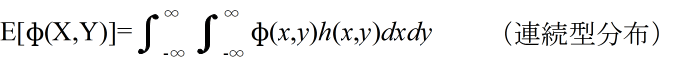
- を φ(X, Y) の期待値という.
- X や Y に対する平均や分散も,1 変数の場合と同様に定義できます.さらに,2 次元分布に対しては,2 変数間の関係の程度を表す量として次のものが定義されています.
- [定義] 確率変数 X,Y に対して,
- σxy = C[X, Y] = E[(X - E[X])(Y - E[Y])] = E[(X - μx)(Y - μy)]
- を X と Y の共分散( covariance )という.
- 実際の問題では,共分散の代わりに,-1 ~ 1 の値をとるように正規化した相関係数( correlation coefficient )
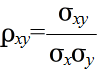
- が使用される場合が多いと思います.相関係数は,相関がある場合(変数 X が大きくなると変数 Y も大きくなるような場合)には 1 に近く,負の相関がある場合(変数 X が大きくなると変数 Y は小さくなるような場合)には -1 に近くなり,相関がない場合は 0 になります.値を解釈する目安は,概略,以下のようになります.
- 0.0 ≦ |ρxy| ≦ 0.2 : ほとんど相関がない
- 0.2 ≦ |ρxy| ≦ 0.4 : やや相関がある
- 0.4 ≦ |ρxy| ≦ 0.7 : かなり相関がある
- 0.7 ≦ |ρxy| ≦ 1.0 : 強い相関がある
- 最後に,2 次元分布に対する平均,分散,及び,共分散の性質をあげておきます.
- [定理 3.4] 確率変数 X,Y に対して以下の式が成立する.
- (1) E[aX + bY] = aE{X} + bE[Y]
- (2) V[aX + bY] = a2V[X] + 2abC[X, Y] + b2V[Y]
- (3) C[X, Y] = E[XY] - E[X]E[Y]
- (1) E[aX + bY] = aE{X} + bE[Y]
- 例えば,2 個のサイコロを振る場合,それぞれのサイコロの目を X 及び Y として,X = 1,Y = 5 となるような確率を考えるように,同時に 2 つの試行を行ったときの確率分布を調べたい場合があります.このような確率分布を 2 次元確率分布といいます.これに対して,今まで取り扱ってきた 1 変数の場合を 1 次元確率分布といいます,2 次元確率分布に対しても,1 次元確率分布の場合と同様に確率密度関数を定義できます.
- 確率変数の独立性
- 先に述べた統計的独立の概念は,確率分布を使用しても表現することができます.
- [定義] 確率変数 X,Y の同時確率密度関数を h(x, y),X の周辺確率密度関数を f(x),及び,Y の周辺確率密度関数を g(y) としたとき,すべての x,y に対して,
- h(x, y) = f(x)g(y)
- が成立するとき,確率変数 X と Y は独立であるという.
- 例 3.5: 例 3.4 について考えてみます.明らかに,10 硬貨の表裏は,100 円硬貨の表裏とは無関係に決まります.従って,X 及び Y の周辺確率密度関数,
- f(x) = 1 / 2 ( 0, 1 のとき)
- = 0 (その他)
- g(y) = 1 / 2 ( 0, 1 のとき)
- = 0 (その他)
- を使用して,同時確率密度関数は,
- h(x, y) = f(x)g(y)
- のように表現でき,2 つの変数は独立であると言えます.
- [定理 3.5] 確率変数 X,Y が独立なとき,
- E[XY] = E[X]E[Y]
- が成立する.
- 上の定理より,明らかに,確率変数 X,Y が独立なときは,共分散や相関係数は 0 になります.
- 先に述べた統計的独立の概念は,確率分布を使用しても表現することができます.
- [定義]
- (1) 平均値: x = ( x1 + x2 + ・・・ + xN) / N
- (2) 中央値(メディアン,median ): データを大きさの順に並べたときの中央の値(データの個数が偶数のときは,中央の 2 つの値の平均)
- (3) 最頻値(モード,mode ): データの中に最も多く現れるデータの値
- (4) 分散: s2 = {(x1 - x)2 + (x2 - x)2 + ・・・ + (xN - x)2} / N
- (5) 標準偏差: s
- (1) 平均値: x = ( x1 + x2 + ・・・ + xN) / N
- [定義]
- (1) 共分散: sxy = {(x1 - x)(y1 - y) + (x2 - x)(y2 - y) + ・・・ + (xN - x)(yN - y)} / N
- (2) 相関係数: ρxy = sxy / (sxsy)
- (1) 共分散: sxy = {(x1 - x)(y1 - y) + (x2 - x)(y2 - y) + ・・・ + (xN - x)(yN - y)} / N
- [定理 4.1] 直線,
- y = ax + b
- から,N 個の各点 (xi, yi) ( i = 1, 2, ・・・, N )への y 軸方向の距離の 2 乗和,
- L = (ax1 + b - y1)2 + (ax2 + b - y2)2 + ・・・ + (axN + b - yN)2
- を最小にするように a 及び b の値を決めると以下のようになる.
- a = sxy / sx2, b = y - ax
- [定義] 定理 4.1 において,直線,
- y = ax + b
- を変量 y の変量 x に対する回帰直線といい,定数 a を回帰係数,b を定数項という.
- [定義] 調査や観測の対象となる属性を持つすべての個体の集合を母集団という.母集団から取り出された一部のデータの集合を標本といい,データの数を標本の大きさという.また,母集団の平均,分散,標準偏差などを母平均,母分散,母標準偏差といい,一般に母集団の特性値を母数という.
- 母集団からランダムに標本を取り出すことを無作為抽出( random sampling )といい,無作為抽出によって取り出された標本を無作為標本(任意標本)という.
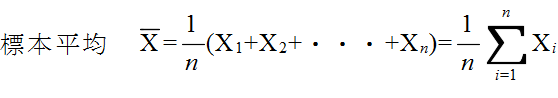
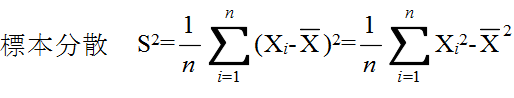

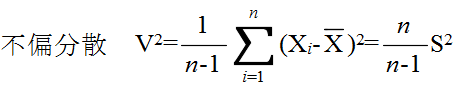
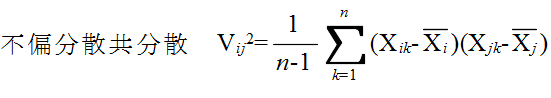
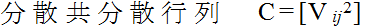
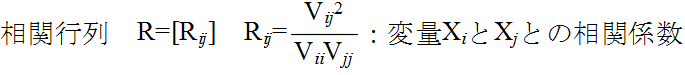
- [定理 4.2] 確率変数 X1, X2, ・・・, Xn が互いに独立で,平均が μ,分散が σ2 の同じ分布に従うとき,確率変数,
- X = (X1 + X2 + ・・・ + Xn) / n
- の平均及び分散は以下のようになる.
- E[X] = μ, V[X] = σ2 / n
- [定理 4.3] 中心極限定理 確率変数 X1, X2, ・・・, Xn が互いに独立で,平均が μ,分散が σ2 の同じ分布に従うとき,それらの平均 X の確率分布は,n を十分大きくすれば,正規分布 N(μ, σ2/n) で近似される.
- 分布が平均に対して左右対称の場合: n ≧ 30
- 分布が平均に対して左右非対称の場合: n ≧ 50
- [定義] 未知の母数に対して,未知母数 θ が a ≦ θ ≦ b となる確率が (1 - α),つまり,
- P(a ≦ θ ≦ b) = 1 - α
- となるように決定した [a, b] を信頼水準( confidence level,信頼係数,信頼率)が (1 - α) である信頼区間,または,100(1 - α)%信頼区間という.
- 母平均の区間推定(母分散 σ2 が既知の場合)
- 母集団が,正規分布 N(μ, σ2) に従っているものとします.ただし,標本の大きさ n が大きいときは,必ずしも正規分布である必要はありません.このとき,中心極限定理により,標本平均 X は,N(μ, σ2/n) の正規分布をします.従って,
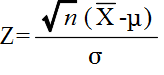
- は,標準正規分布 N(0, 12) に従います.A(α) を標準正規分布の α 点とすると,
- P(|Z| ≦ A(α/2)) = 1 - α
- という関係が成り立ちます.つまり,
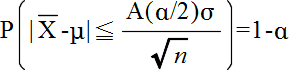
- となります.このことより,推定の信頼水準を (1 - α) とすると,母平均の信頼区間は,以下のようになります.この式は,標本平均 X が得られたとき,母平均 μ が以下の区間に入る確率が (1 - α) であることを意味します.
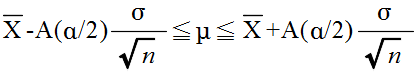
- 母平均の区間推定(母分散 σ2 が未知の場合)
- [定理 4.4] n 個の確率変数 X1, X2, ・・・, Xn が平均 μ の同じ正規分布に従い,互いに独立ならば,その標本分散を S2 としたとき,
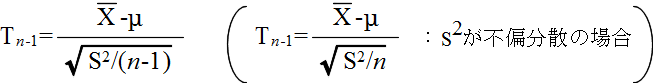
- で定義される確率変数 Tn-1 が,母分散に関係なく,自由度 n-1 の t 分布に従う.
- 標本の大きさが n,標本平均が X,標本分散が S2 であるとします.上の定理を利用することによって,母平均 μ の信頼水準 (1 - α) の信頼区間は,自由度 n-1 の t 分布の α 点を tn-1(α) とすると,以下のようになります.

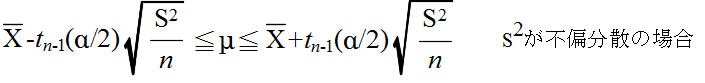
- 母分散の区間推定
- [定理 4.5] n 個の確率変数 X1, X2, ・・・, Xn が同じ正規分布 N(μ, σ2) に従い,互いに独立ならば,
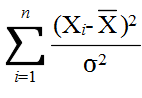
- で定義される確率変数は,自由度 n-1 の χ2 分布に従う.
- 上の定理より,正規母集団から大きさ n の標本を無作為抽出したとき,母分散 σ2 に対する信頼水準 (1 - α) の信頼区間は,自由度 n-1 の χ2 分布の α 点をχ2n-1(α) とすると,以下のようになります.
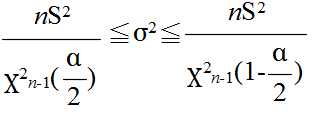
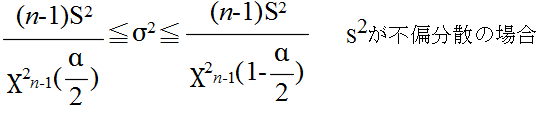
- 例 4.1: 10 個の卵の重さ(単位g)を測ったところ,標本平均は 69.05 g でした(卵全体は正規母集団とする).最初に,母分散 σ2 が既知( = 22 )であるとしたとき,母平均の 95 %信頼区間は正規分布を利用して以下のようになります.
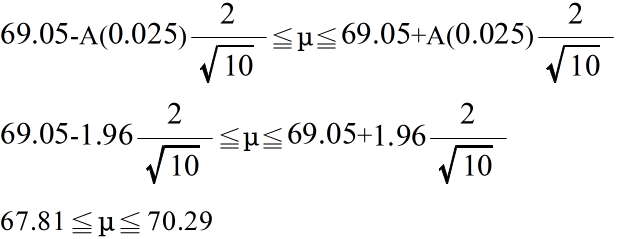
- 次に,母分散 σ2 が未知である場合について考えてみます.標本分散 s2(不偏分散)が 22 であった場合における母平均の 95 %信頼区間を計算してみます.この場合は,自由度 9 の t 分布を利用して以下のようになります.
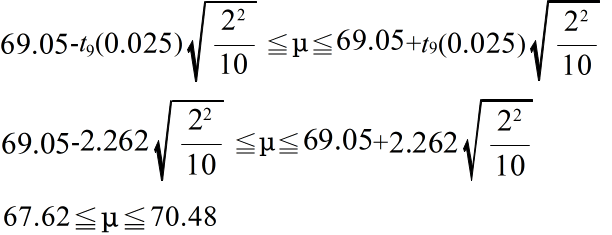
- この例に見るように,同じ信頼区間であっても,情報量が多いほど(この場合は,母分散が既知),信頼区間は短くなります.つまり,より高い精度で母平均を推定できることになります.
- 最後に,母分散に対する信頼区間を求めてみます(当然,母分散は未知).標本分散 s2(不偏分散)が 22 であった場合における母分散の 95 %信頼区間は,自由度 9 の χ2 分布を利用して以下のようになります.
- 最後に,母分散に対する信頼区間を求めてみます(当然,母分散は未知).標本分散 s2(不偏分散)が 22 であった場合における母分散の 95 %信頼区間は,自由度 9 の χ2 分布を利用して以下のようになります.
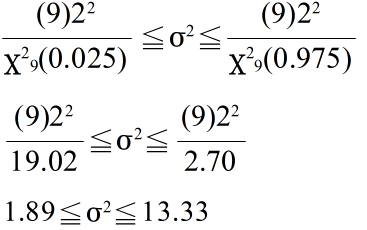
- [定理 4.6] 平均の検定(母分散が既知の場合) 母集団 Ω の母平均 μ に対して,その値が μ0 であるという仮説,つまり,次のような仮説をたてる.
- 帰無仮説 H0: μ = μ0
- 対立仮説 H1: μ ≠ μ0
- 対立仮説 H1: μ ≠ μ0
- このとき,母集団が,正規分布 N(μ, σ2) に従っているものとする(標本の大きさ n が大きいときは,必ずしも正規分布である必要はない).中心極限定理により,標本平均 X は,N(μ, σ2/n) の正規分布をする.従って,
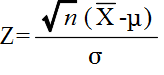
- は,標準正規分布 N(0, 12) をする.そこで,A(α) を正規分布の α 値としたとき,標本から計算された z が不等式,
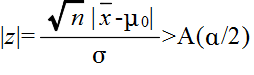
- を満たすならば,有意水準 α で,仮説 H0 を棄却する.
- [定理 4.7] 平均の t 検定(母分散が未知の場合) 正規分布 N(μ, σ2) に従っている母集団 Ω の母平均 μ に対して,その値が μ0 であるという仮説,つまり,次のような仮説をたてる.
- 帰無仮説 H0: μ = μ0
- 対立仮説 H1: μ ≠ μ0
- 対立仮説 H1: μ ≠ μ0
- このとき,Ωからの大きさ n の標本平均を X,標本分散を S2 としたとき,
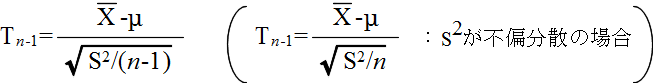
- で定義される確率変数 Tn-1 が,自由度 n-1 の t 分布に従う.そこで,tn-1(α) を自由度 n-1 の t 分布の α 値としたとき,標本から計算された t が不等式,
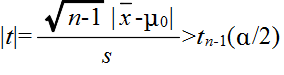
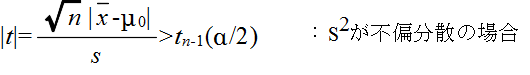
- を満たすならば,有意水準 α で,仮説 H0 を棄却する.
- 例 4.2: ある機械で製造する製品の長さに対する規格が 200 mm であったとします.この機械で製造した製品を 25 個取りだし,その長さを測ったところ,標本平均は 200.81 mm でした(製造した製品全体は正規母集団とする).製品の長さが規格通りか否かを,有意水準 5 %で検定してみます.つまり,次のような仮説を立てます.
- 帰無仮説 H0: 製品の母平均 μ = μ0( = 200 mm )
- 対立仮説 H1: 製品の母平均 μ ≠ μ0( = 200 mm )
- 対立仮説 H1: 製品の母平均 μ ≠ μ0( = 200 mm )
- 最初に,母分散 σ2 が既知( = 22 )である場合について考えてみます.定理 4.6 より,|z| の値を計算すると,|z| = 2.025 となります.この値は,A(0.025) = 1.96 より大きくなりますので,仮説を棄却し対立仮説を受け入れる,つまり,製品の長さは規格に合っていないというのが結論になります.
- 同じ例に対して,製品の長さが規格より大きいか否かを検定する場合はどうでしょうか.この場合は,次のような仮説を立てることになります.
- 同じ例に対して,製品の長さが規格より大きいか否かを検定する場合はどうでしょうか.この場合は,次のような仮説を立てることになります.
- 帰無仮説 H0: 製品の母平均 μ = 200 mm(規格値)
- 対立仮説 H1: 製品の母平均 μ > 200 mm(規格値)
- 対立仮説 H1: 製品の母平均 μ > 200 mm(規格値)
- この場合は,片側検定になりますので,z の値を A(0.05) = 1.645 と比較することになります.z の値 2.025 は A(0.05) より大きいため,先の場合と同様,仮説を棄却し対立仮説を受け入れる,つまり,製品の長さは規格より大きいというのが結論になります.
- では,母分散が未知の場合はどうでしょうか.標本分散 s2(不偏分散)が 22 であった場合に対し,製品の長さが規格通りか否かを,有意水準 5 %で検定してみます.定理 4.7 より,|t| の値を計算すると,|t| = 2.025 となります.この値は,自由度 24 の t 分布の 5 %値 t24(0.025) = 2.06 より小さくなりますので,仮説を受け入れる,つまり,製品の長さは規格通りであるというのが結論になります.
- この例のように,検定結果は,仮説,有意水準,検定方法等によって異なってくる点に注意して下さい.
- では,母分散が未知の場合はどうでしょうか.標本分散 s2(不偏分散)が 22 であった場合に対し,製品の長さが規格通りか否かを,有意水準 5 %で検定してみます.定理 4.7 より,|t| の値を計算すると,|t| = 2.025 となります.この値は,自由度 24 の t 分布の 5 %値 t24(0.025) = 2.06 より小さくなりますので,仮説を受け入れる,つまり,製品の長さは規格通りであるというのが結論になります.
- [定理 4.8] 平均の差に関する検定(母分散が既知の場合) N(μx, σx2) に従う母集団から大きさ m の標本を抽出したときの標本平均を X とし,N(μy, σy2) に従う母集団から大きさ n の標本を抽出したときの標本平均を Y としたとき,2 つの母平均 μx と μyに対して,その値が等しいという仮説,つまり,次のような仮説をたてる.
- 帰無仮説 H0: μx = μy
- 対立仮説 H1: μx ≠ μy
- 対立仮説 H1: μx ≠ μy
- このとき,
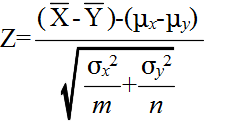
- は,標準正規分布 N(0, 12) をする.そこで,A(α) を正規分布の α 値としたとき,標本から計算された z が不等式,
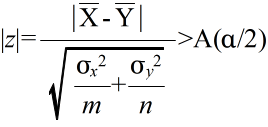
- を満たすならば,有意水準 α で,仮説 H0 を棄却する.
- [定理 4.9] 平均の差に関する t 検定(母分散が未知で,かつ,同じ場合) N(μx, σ2) に従う母集団から大きさ m の標本を抽出したときの標本平均を X,標本分散を Sx2とし,N(μy, σ2) に従う母集団から大きさ n の標本を抽出したときの標本平均を Y,標本分散を Sy2としたとき,2 つの母平均 μx と μyに対して,その値が等しいという仮説,つまり,次のような仮説をたてる.
- 帰無仮説 H0: μx = μy
- 対立仮説 H1: μx ≠ μy
- 対立仮説 H1: μx ≠ μy
- このとき,
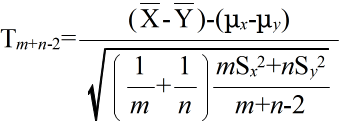
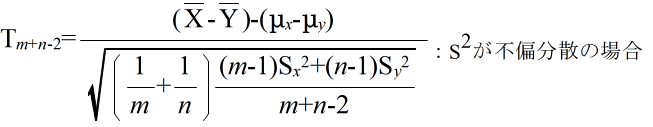
- で定義される確率変数 Tm+n-2 が,自由度 m+n-2 の t 分布に従う.そこで,tm+n-2(α) を自由度 m+n-2 の t 分布の α 値としたとき,標本から計算された t が不等式,
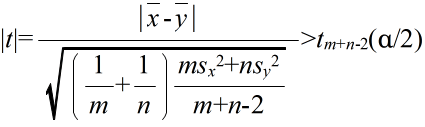
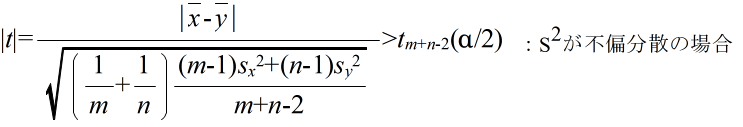
- を満たすならば,有意水準 α で,仮説 H0 を棄却する.
- 例 4.3: 同じ製品を製造する機械 x 及び y があります.各機械から 31 個の製品を取りだし,その長さを測ったところ,各々の標本平均は 200.53 mm,及び,199.11 mm,また,標本分散(不偏分散)は 2.02 mm,及び,1.52 mm でした(製造した製品全体は正規母集団とし,各機械の母分散は未知であるが等しい).2 つの機械で製造した製品の長さが等しいか否かを,有意水準 1 %で検定してみます.つまり,次のような仮説を立てます.
- 帰無仮説 H0: 機械 x の母平均 μx = 機械 y の母平均 μy
- 対立仮説 H1: 機械 x の母平均 μx ≠ 機械 y の母平均 μy
- 対立仮説 H1: 機械 x の母平均 μx ≠ 機械 y の母平均 μy
- 定理 4.9 より,|t| の値を計算すると,|t| = 3.16 となります.この値は,自由度 60 の t 分布の 1 %値 t60(0.005) = 2.66 より大きくなりますので,仮説を棄却する,つまり,2 つの機械によって製造した製品の長さは等しくないというのが結論になります.
- [定理 4.10] 分散の検定 n 個の確率変数 X1, X2, ・・・, Xn が同じ正規分布 N(μ, σ2) に従い,互いに独立ならば,
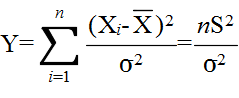
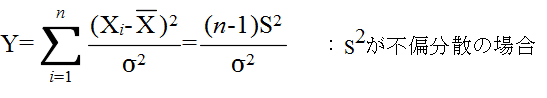
- で定義される確率変数は,自由度 n-1 の χ2 分布に従う.そこで,分散に対する検定を行うには,まず,仮説
- 帰無仮説 H0: σ = σ0
- 対立仮説 H1: σ ≠ σ0
- 対立仮説 H1: σ ≠ σ0
- を設定する.自由度 n-1 の χ2 分布の α 点をχ2n-1(α)としたとき,標本から計算された y が不等式,
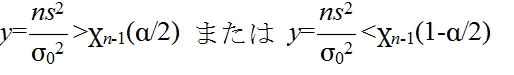

- を満たすならば,有意水準 α で,仮説 H0 を棄却する.
- [定理 4.11] 分散の比に対する検定 N(μx, σ2) に従う母集団から大きさ m の標本を,また,N(μy, σ2) に従う母集団から大きさ n の標本を抽出したとき,
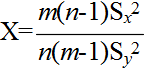
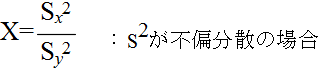
- で定義される確率変数 F(m-1, n-1) が,自由度 (m-1, n-1) の F 分布に従う.そこで,2 つの正規母集団から抽出されたデータに対して,それらの母分散が等しいという仮説,つまり,次のような仮説をたてる.
- 帰無仮説 H0: σx2 = σy2
- 対立仮説 H1: σx2 ≠ σy2
- 対立仮説 H1: σx2 ≠ σy2
- このとき,自由度 (m-1, n-1) の F 分布の α 点を F(m-1, n-1)(α)としたとき,標本から計算された x が不等式,

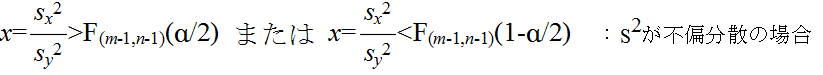
- を満たすならば,有意水準 α で,仮説 H0 を棄却する.
