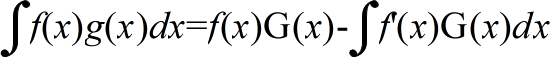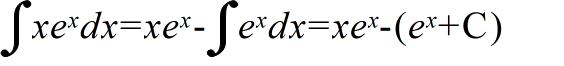微分積分

　　微分や積分は様々な分野で利用され，非常に重要な概念です．難しい概念のように思われがちですが，決してそうではありません．以下に述べるように，微分・積分は，我々の日々の生活の中でほとんど意識することなく利用しているような簡単な概念です．また，利用することなしでは生きていくことすら困難になるといっても過言ではありません．

　　例えば，山へ登っている途中で道に迷った場合について考えてみます．また，霧のため，周りはほとんど見えないものとします．尾根へたどり着けば道が存在すると思われるので，その方向（高い方）へ登っていきたいとします．このとき，どのような方向に向かえばよいでしょうか．周りがほとんど見えなくても，足下近傍の情報から，どちらの方向へ向かえば高い方へ向かうかの見当が付きます．このとき使用している情報 ”傾斜”は，正に，位置を微分するという動作から得られたものです．

　　今，A という場所から B という目的地に向かって歩いていたとします．A から B までの距離は分かっており，1 時間程度で行ける場所だとします．30 分程度歩いたとき，「これで半分来たか．あと，30 分程度で着くだろう」といったようなことを考えるはずです．このような推論が可能であるためには，歩く速度－位置を微分したもの－を知っている必要があります．また，30 分歩いた時の移動距離－速度を 30 分間積分したもの－も知っている必要があります．

　　以上の例で述べたように，微分は変化率に基づいた予測のために，また，積分は過去の行動を積み重ねた結果を表す（和の拡張）ために使用されます．我々は，微分や積分を，何の困難さもなく普段使用しているはずです．ここでは，これらの概念について，もう少し精密に検討していきます．

１．関数の極限と連続性

　　変数 x の値が決まると，変数 y の値が決まるような規則が存在する時，y は x の関数であると言い，

y = f(x)

のように記述します．このとき，x を独立変数，また，y を従属変数と呼びます．さらに，y の値を決めることができる x の値の集合をこの関数の定義域，また，それらの値に対して決まる y の値の集合を値域と言います．なお，ここでは，以後，x 及び y は実数値を取るものと仮定します．

　　例えば，以下に示すような関数の定義域及び値域は，各関数の右側に示したようになります．

y = x　　定義域：(-∞, ∞)，　値域：(-∞, ∞)
y = x²　　定義域：(-∞, ∞)，　値域：[0, ∞)
y = -x^0.5　　定義域：[0, ∞)，　値域：(-∞, 0]

なお，ここで，(, ) は，開区間を表す記号であり，a < x < b であるような実数 x の全体を (a, b) のように表します．また， [, ] は，閉区間を表す記号であり，a ≦ x ≦ b であるような実数 x の全体を [a, b] のように表します．上に示す例のように，片側だけに () や [] を使用することも可能です．

　　次に，関数の極限について考えてみます．

［定義］　関数 f(x) において，x が a に限りなく近づくとき（ x → a と表す），f(x) の値がある定数 α に限りなく近づくならば，
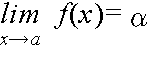
と表し，α を x → a のときの f(x) の極限値という．また，このとき，関数 f(x) は α に収束するという．

　　一般に，a が有限値の場合，a へは 2 つの方向から近づくことが可能です．つまり，a より大きい値から a に近づく方法と，a より小さい値から a に近づく方法です．これらを明確に表すためには，それぞれ，「 x → a+0 」及び「 x → a-0 」と記述し（ a が 0 の時は a を省略），右側極限値及び左側極限値と呼びます．また，併せて，片側極限値と呼びます．これらの値は常に存在するとは限りませんが，それらが存在し，かつ，その値が等しい時，「 x → a 」と記述し，それが関数の極限値になります．

　　微分法や積分法において，関数の連続性は重要な概念です．上で述べた関数の極限値を利用して関数の連続性を以下に示すように定義します．

［定義］　関数 y = f(x) が x = a において連続であるとは，以下に示す 3 つの条件を満足することである．

(1) f(x) が定義されている（例えば，f(a) = α とする）

(2) x → a のときの f(x) の極限値 β が存在する

(3) α = β である
関数 f(x) が区間 I 内のすべての点で連続である時，関数 f(x) は区間 I で連続であるという．ただし，閉区間の端点においては，極限値を片側極限値で定義するものとする．

　　直感的に明らかですが，連続関数に対して以下に示す定理が成立します．

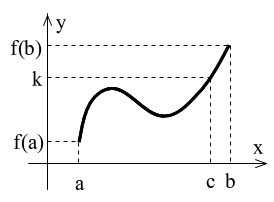
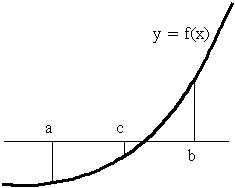
［定理］　（中間値の定理） 関数 f(x) が閉区間 [a, b] で連続であり，f(a) ≠ f(b) であるならば，: f(c) = k　　(a < c < b)
となる数 c が少なくとも一つ存在する．

２．微分法

２．１微分法：定義と公式

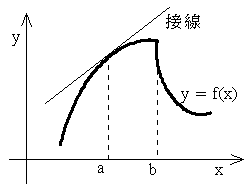
［定義］　曲線 y = f(x) が与えられたとき，曲線上の点 A(a, f(a)) において
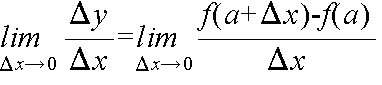
が存在する（有限）ならば，この値を f(x) の x = a における微分係数といい，
で表す．このとき，f(x) は x = a で微分可能であるという．また，関数 f(x) がある区間の任意の数 a に対して，x = a で微分可能であるとき，f(x) はその区間で微分可能であるという．

　　正に，この微分係数が，先に述べた例における山の傾斜に対応しています．Δx が，足下近傍ということになります．

　　微分係数 f’(a) は，右図に示すように，x = a における接線の傾きに相当します．また，x = a において微分係数が存在することは，曲線 y = f(x) が，x = a でなめらかに変化していることを意味しています．例えば，x = b のように，曲線が折れ曲がっているような点では，微分係数は存在しません．

［定義］　関数 f(x) がある区間で微分可能であるとき，先の a は区間内の任意の数であるから，変数 x と考えて，
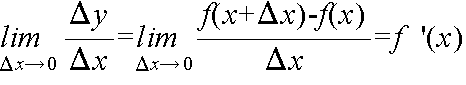
を定義する．この f’(x) を f(x) の導関数といい，導関数 f'(x) を求めることを，f(x) を（ x で）微分するという．f(x) の導関数を表すのに，
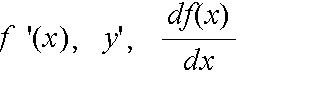
等と書く．

　　導関数の導関数も，同様に定義可能です．

［定義］　導関数の導関数は 2 階の（または，2 次の）導関数と呼ばれ，
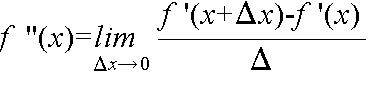
と表す．一般に，n 階の（または n 次の）導関数を
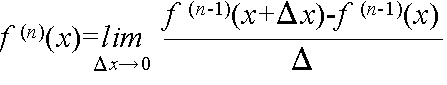
と表す．また，
とも表す．

　　以下，よく使用する微分法の公式をあげておきます．

２．２導関数の応用

　　以下に述べる定理や定義は，関数の形を判別したり，最大値や最小値を求めるときに使用されます．

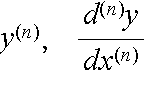
　　まず，平均値の定理ですが，この定理の意味することは下図から明らかだと思います．

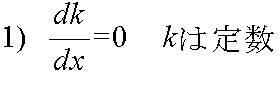
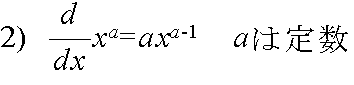
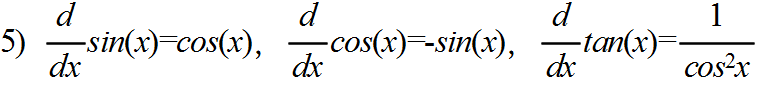
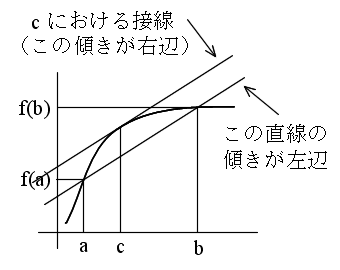
［定理］　（平均値の定理） 関数 f(x) が閉区間 a ≦ x ≦ b （ a < b ）で微分可能ならば，
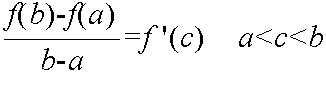
となる数 c が存在する．

［定理］　関数 f(x) が閉区間 a ≦ x ≦ b （ a < b ）で微分可能とする．

(1) 閉区間 a ≦ x ≦ b でつねに f’(x) > 0 ならば，f(x) は単調増加する．

(2) 閉区間 a ≦ x ≦ b でつねに f’(x) < 0 ならば，f(x) は単調減少する．

(3) 閉区間 a ≦ x ≦ b でつねに f’(x) = 0 ならば，f(x) は定数である．

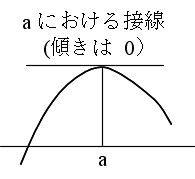
［定義］　f(a) が x = a の近傍で最大（最小）であるとき， f(x) は x = a で極大（極小）になるといい，f(a) を極大値（極小値）という．また，極大値と極小値をあわせて極値といい，f(x) が x = a で極値をもつならば，f’(a) = 0 である．

　　次は，平均値の定理の拡張です．特に，2 次，または，3 次以上の項を無視して，関数を 1 次多項式や 2 次多項式で近似することはしばしば行われますので，非常に重要な定理です．

［定理］　（テイラーの定理） 関数 f(x) が閉区間 [a, x] で n 回微分可能ならば，
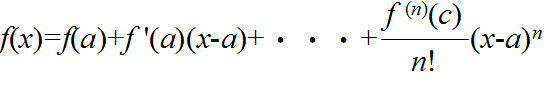
となる数 c （ a < c < x ）が存在する．ここで，最後の項（ R_n とする）を剰余項という．n　を限りなく大きくするとき，lim R_n = 0 となるならば，f(x) は，
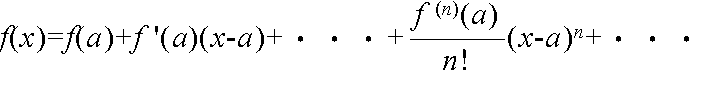
のように無限級数展開される．これを関数 f(x) のテイラー展開という．特に，a = 0 のとき，マクローリン展開と呼ばれる．

　　以下に示すのは，関数のマクローリン展開の例です．マクローリン展開は，x が小さな時，関数を線形近似（ x の 1 次の多項式で表す）したいようなときよく使用されます．以下の例において，右辺の 2 次以上の項を無視しても，x が小さいときは左辺と右辺の値がほぼ一致することを確認できるはずです．

　　ここで，導関数の具体的利用方法について考えてみます．例として，非線形方程式を取り上げます．非線形方程式を解く方法の一つとして二分法が存在します．関数 f(x) が区間 [a, b] で連続で，かつ，根が 1 つだけ存在するような場合に利用できる方法です（下の左図参照）．二分法では，まず，区間 [a, b] の中点（図の c ）における関数値を計算します．次に，区間 [a, c]，及び，区間 [c, b] のどちらに解が存在するかによって，区間 [a, c]，または，区間 [c, b] の中点における関数値を計算します．このことを，区間の幅が十分小さくなるまで続けることによって解を求めます．このように，二分法は，区間を半分にするという操作を機械的に繰り返すだけの方法ですので，この方法が適用できる条件さえ満たしていれば必ず収束し，解を得ることができます．しかし，一般に収束までに時間が掛かります．

　　次の方法として，Newton 法（ニュートン法）について考えてみます．Newton 法によるアルゴリズムは以下の通りです．上の右図に示すように，まず，初期値 x₀ を与えます．次に，f(x₀) を計算し，(x₀, f(x₀)) における接線が x 軸と交わる点を x₁ とします．再び，x₁ から同様の手続きを繰り返し，収束するまで続けます．「接線が x 軸と交わる点を求める」という操作は，微分係数を利用して現時点における曲線の傾きを求め，「そのまま同じ傾きが続くようであれば，x 軸とはここで交わるであろう」という予測処理を行っていることになります．従って，曲線の変化が予測どおり，又は，予測に近い状況であれば，非常に早く解を求めることができます．しかし，予測から大きく外れた場合は，とんでもないことが起こる可能性もあります．

　　次に，以上述べた方法を利用して，上に示す非線形方程式，

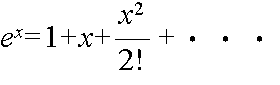
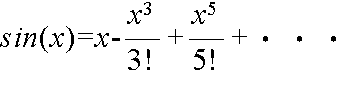
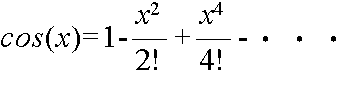
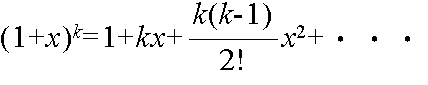
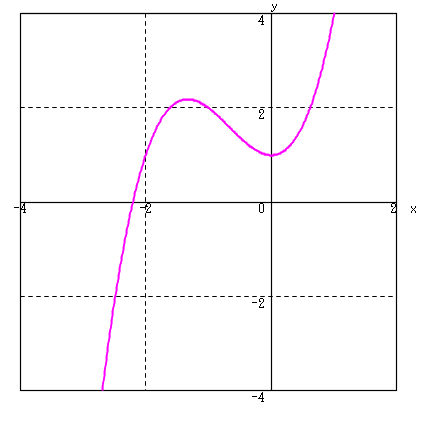
f(x) = x³ + 2x² + 1

の解を求めてみます．まず，最初の区間を [-4.0, 0.0] として，二分法によって解を求めると，36 回の繰り返しで以下のような結果が得られます．なお，繰り返しは，区間の幅が 1.0e-10 以下になるまで続けました．

x = -2.205569430429   f(x) = -0.000000000164

　　次に，初期値 x₀ を -4.0 として，Newton 法によって解を求めると，たった 7 回の繰り返しで以下のような結果が得られました．

x = -2.205569430401   f(x) = -0.000000000000

しかし，二分法においては，初期区間を多少変えても結果に大きな影響は出ませんが，Newton 法では初期値によって大きく異なります．つまり，予測が外れた場合は，解が求まらない，解を求めるのに時間が掛かるといって状況が発生します．例えば，x₀ を 0.0 とした場合は解が求まりませんし，また，x₀ をｰ0.15 に設定すると，収束回数が 42 回になってしまいました．

　　このように，微分の利用は非常に強力ですが，場合によっては，予期しない結果になります．多くの分野で微分は利用されていますが，いずれの分野においても，微分は予測作用素であり，予測が正しい場合は強力であるが，予測が外れた場合は非常に危険であるといったことを常に理解しておく必要があります．

２．３偏微分

［定義］　関数 z = f(x, y) において，y を一定にして x を動かすと，z = f(x, y) は x だけの関数となる．このとき，x の関数の導関数
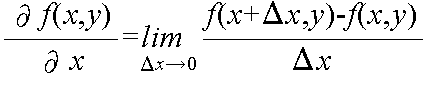
が存在するならば，これを x に関する偏導関数という．このとき，関数 f(x, y) は x に関して偏微分可能であるという．また，y に関する偏導関数も同様に定義できる．x に関する偏導関数を表すのに，
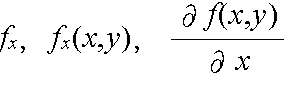
等とも書く．
　　2 階，3 階，さらに，n 階の偏導関数も定義できる．2 変数関数 f(x, y) の偏導関数 f_x(x, y)， f_y(x, y) は x， y の関数であるから，これをさらに，x または y で偏微分することによって，2 階の偏導関数: f_xx(x, y)， f_xy(x, y)， f_yx(x, y)， f_yy(x, y)
ができる．これらを表すのに，
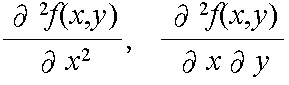
等とも書く．

３．積分法

３．１積分法：定義と公式

［定義］　関数 f(x) に対して，F'(x) = f(x) となる関数 F(x) を f(x) の原始関数または不定積分という．f(x) の不定積分を
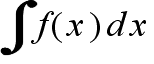
と表し，これを求めることを f(x) を積分するという．F(x) を f(x) の不定積分の一つとすると，f(x) と任意の不定積分は，F(x) と定数の違いしかない．すなわち，
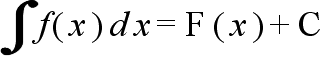
で表される．このとき，定数 C を積分定数という．

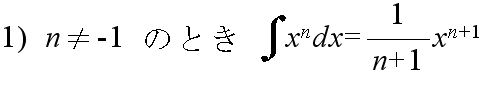
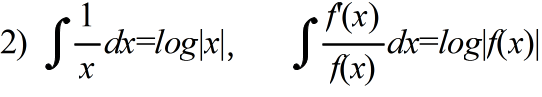
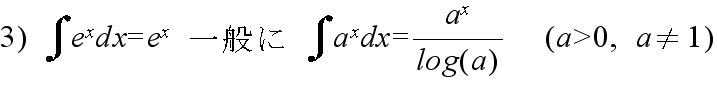
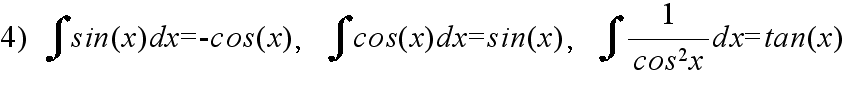
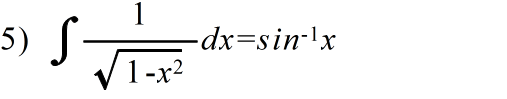
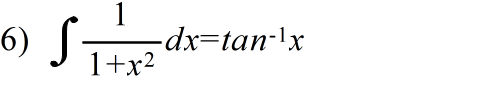
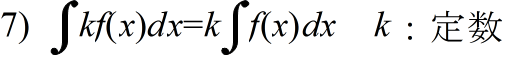
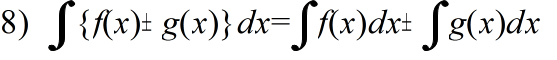
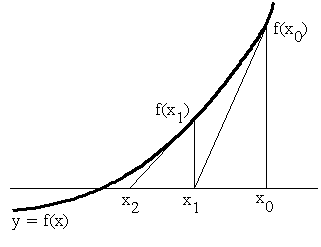
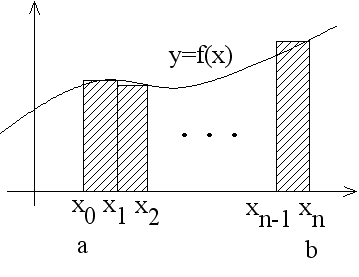
　　以下，代表的な関数に対する積分法の公式をあげておきます．なお，以下の公式において，積分定数は省略してあります．

　　以下に述べるのが，定積分の定義です．

［定義］　閉区間 a ≦ x ≦ b で定義されている関数 f(x) を考える．下図に示すように，その関数の閉区間 a ≦ x ≦ b を n 等分して，
その分点を: a = x₀， x₁， x₂，･･･， x_n = b
とし，
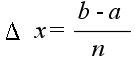
とすると，
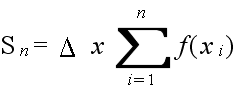
は，n 個の長方形の和となる（図の斜線部）．n が限りなく大きくなれば，数列 {S_n} は，曲線 y = f(x)， 2 直線 x = a， x = b ，及び， x 軸で囲まれた面積 S に限りなく近づく．数列 {S_n} の極限値
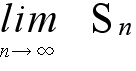
を，f(x) の a から b までの定積分といい，
と表す．

　　以下，代表的な定積分の公式をあげておきます．なお，定積分の結果を確認したいような場合は，「数値積分」を利用可能です．

　　次に，3 次元空間における定積分について考えてみます．2 変数の関数 f(x,y) が xy 平面上の領域 D において連続であるとします．このとき，領域 D を矩形の小領域 D_ij （その中心の座標を (x_i,y_j) とする）に分割し，その 2 辺の長さを Δx_i，Δy_j とします．このとき，

は，矩形を底面とした高さ f(x_i,y_j) の直方体の体積になります．従って，分割を限りなく小さくし，領域 D 上で上記の値をすべて加えた結果は，曲面 z = f(x,y) と xy 平面の間で領域 D の上にある部分の体積になります．これを，

と記述し，領域 D 上の 2 重積分とよびます．同じような方法で，3 重以上の多重積分も定義可能です．

３．２置換積分法と部分積分法

　　積分の場合，微分とは異なり，たとえ原始関数が存在したとしても，それを簡単に求めることができない場合が多く存在します．例えば，積分，

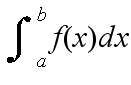
について考えてみます．明らかに，前節で述べた公式をそのまま適用することによっては積分することができません．このような積分を行うのに有用な方法として置換積分法が存在します．

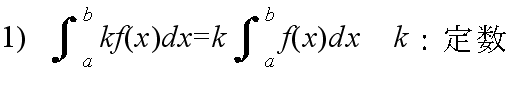
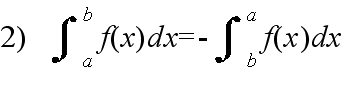
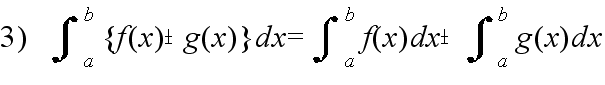
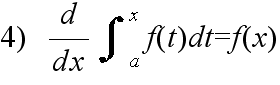
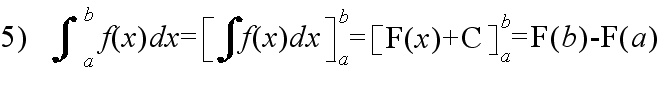
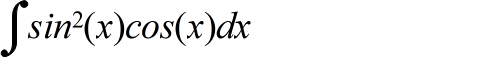
［定理］　（置換積分法） 連続な関数 f(x) に対して，x = φ(t) とおくとき，φ(t) が微分可能ならば，以下の関係が成立する．

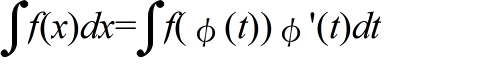
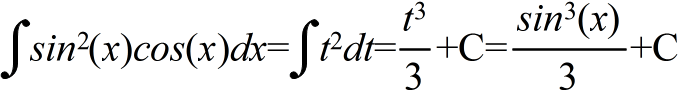
　　例えば，上の例において，sin(x) = t と置くと，cos(x)dx = dt となりますから，以下に示すようにして積分することが可能です．

　　次は，部分積分法に関する定理です．

［定理］　（部分積分法） 2 つの関数 f(x)，g(x) において，f'(x)，g(x) が連続であるとき，g(x) の 1 つの原始関数を G(x) とすると，以下に示す関係が成立する．

　　部分積分法の例として，積分，

について考えてみます．この場合，x = f(x)，e^x = g(x) とすると，G(x) = e^x となり，上の定理を適用でき，その積分は以下に示すようになります．