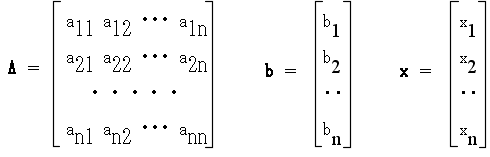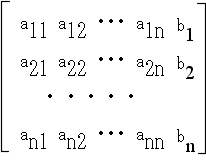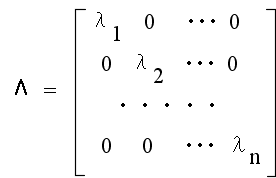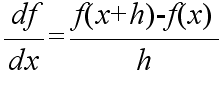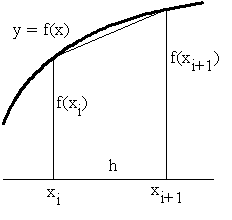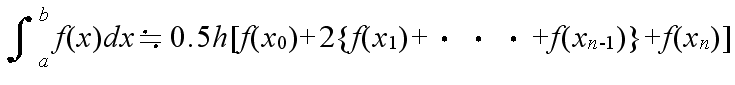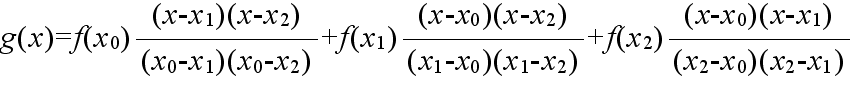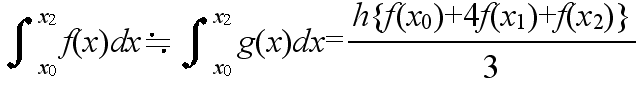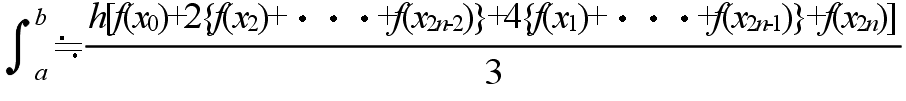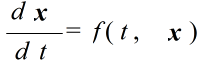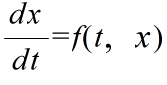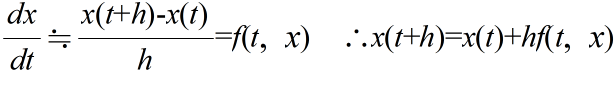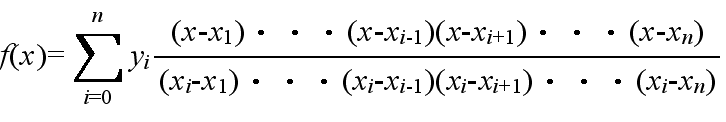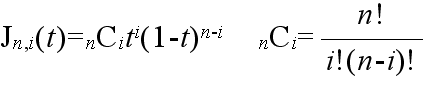数値計算

1. １．連立 1 次方程式と逆行列
   1. １．１ ガウス－ジョルダンの消去法
2. ２．非線形方程式
   1. ２．１ 二分法
   2. ２．２ ニュートン法（ Newton 法）
   3. ２．３ セカント法
3. ３．代数方程式と行列の固有値・固有ベクトル
   1. ３．１ ベアストウ法
   2. ３．２ 行列の固有値（フレーム法＋ベアストウ法）
   3. ３．３ 実対称行列の固有値・固有ベクトル（ヤコビ法）
   4. ３．４ 最大固有値と固有ベクトル（べき乗法）
4. ４．数値微分
5. ５．数値積分
   1. ５．１ 台形則
   2. ５．２ シンプソン則
6. ６．常微分方程式
   1. ６．１ ルンゲ・クッタ法
7. ７．補間法
   1. ７．１ ラグランジュ補間法
   2. ７．２ スプライン補間法
   3. ７．３ ベジエ曲線

１．連立 1 次方程式と逆行列

１．１ ガウス－ジョルダンの消去法

C/C++によるプログラム例　→　

JavaScript 版では，データを変更して，連立方程式の解，逆行列，行列の乗算，及び，行列式の値を計算し，その結果を画面上で得ることも可能です．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「連立線形方程式と逆行列」をご覧ください．

　　以下に示すような連立一次方程式の解を求める方法について検討します．

a₁₁x₁ + a₁₂x₂ + ･･･ a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + ･･･ a_2nx_n = b₂

　　　　　　　・・・・・

a_n1x₁ + a_n2x₂ + ･･･ a_nnx_n = b_n

上式は，行列 A，b，及び，x を

のように定義すれば，以下のように書くことができます．

Ax = b

この方程式の解は，形式的に，A の逆行列を左から掛け，

x = A^-1b

のようにして求めることができます．そこで，拡張された行列

を考え，左側の n×n の部分が単位行列になるような操作を行えば，最後の列に解が求まることになります．

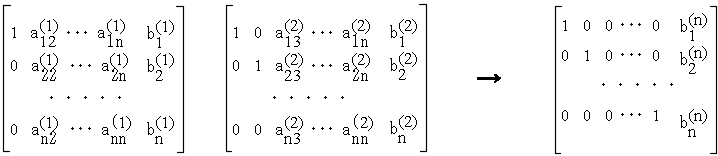
　　ガウス－ジョルダンの消去法は，この操作をコンピュータ上で行うものです．まず，拡張された行列の 1 行目の各要素を a₁₁ で割ります．次に，a₂₁ の値が 0 になるように，1 行目を何倍かして，2 行目に加えます（ 2 行目から引きます）．3 行目以降に対しても，同様の操作を繰り返します．この結果，下に示す図の最初の状態になるはずです．

次に，2 行目を a⁽¹⁾₂₂ で割った後同様の操作を行えば，上図の中央のような状態になります．以下，同様の操作を繰り返すことによって，上図の右端の状態になり，解が求まることになります．

　　以上の操作によって，場合によっては，問題が発生します．つまり，a₁₁，a₂₂ 等が 0 になる場合です．この場合は，行を入れ替え，a_ij の値が最大になるものが a_ii になるようにします．この a_ii のことを，ピボット要素といいます．ピボット要素が 0 であるとき（ある値より小さいとき）は，逆行列が存在しない（行列 A のランクが n より小さい）ことになります．

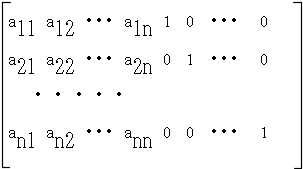
　　また，拡張された行列において，b の部分を単位行列で置き換えれば，つまり，次のようにすれば，後半の n×n の部分に行列 A の逆行列が求まることになります．

２．非線形方程式

　　この節では，非線形方程式 f(x) = 0 の根を求める方法について説明します．

２．１ 二分法

C/C++によるプログラム例　→　

JavaScript 版では，JavaScript の仕様に適合した形で解を求めたい式を入力することによって，任意の非線形方程式の解を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「非線形方程式（二分法）」をご覧ください．

　　関数 f(x) が区間 [a, b] で連続で，かつ，根が 1 つだけ存在するような場合に利用できる方法です．このとき，以下のような関係が成立する必要があります．

f(a) f(b) < 0

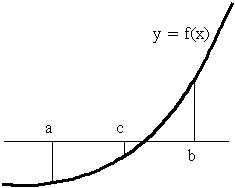
　　二分法のアルゴリズムは以下に示す通りであり，徐々に解の存在区間を狭めることによって解を求める方法です（上図を参照）．一般に，収束は遅いですが，上記の条件を満たせば必ず解に到達します．

1. 区間 [a, b] の中点： c = 0.5 * (a + b) に対し，f(c) の値を計算

2. f(a) f(c) < 0 なら
   b = c，f(b) = f(c)
   そうでなければ
   a = c，f(a) = f(c)

3. |b - a| < ε ならば終了する．そうでなければ，1 に戻る．

２．２ ニュートン法（ Newton 法）

C/C++によるプログラム例　→　

JavaScript 版では，JavaScript の仕様に適合した形で解を求めたい式及びその微分を入力することによって，任意の非線形方程式の解を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「非線形方程式（ニュートン法）」をご覧ください．

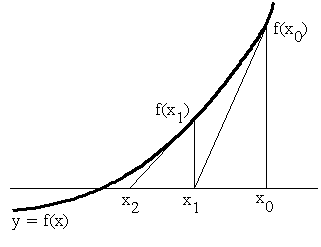
　　ニュートン法（ Newton 法）によるアルゴリズムは以下の通りです．上図に示すように，まず，初期値 x₀ を与えます．次に，f(x₀) を計算し，(x₀, f(x₀)) における接線が x 軸と交わる点を x₁ とします．再び，x₁ から同様の手続きを繰り返し，収束するまで続けます．一般的に記述すれば，以下のようになります．適切な初期値を設定すれば，非常に速く解を求めることが可能です（勿論，関数の形にもよりますが）．

x_n+1 = x_n - f(x_n) / f'(x_n)

収束判定方法としては，以下のような方法があります．

|x_n+1 - x_n| < ε

|f(x_n+1) - f(x_n)| < ε

|f(x_n)| < ε

多次元（x がベクトル）の場合に対する C/C++ によるプログラム例　→　

JavaScript 版では，JavaScript の仕様に適合した形で解を求めたい式及びその微分を入力することによって，任意の非線形方程式の解を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，1 次元の場合と同様，「プログラミング言語の落とし穴」第 9 章の「非線形方程式（ニュートン法）」をご覧ください．

２．３ セカント法

C/C++によるプログラム例　→　

JavaScript 版では，JavaScript の仕様に適合した形で解を求めたい式を入力することによって，任意の非線形方程式の解を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「非線形方程式（セカント法）」をご覧ください．

　　セカント法は，二分法と同様，関数 f(x) が区間 [a, b] で連続で，かつ，根が 1 つだけ存在するような場合に利用できる方法です．ただし，二分法とは異なり，中点の関数値ではなく，Newton 法における計算方法の微分を差分で置き換えた方法を利用します．アルゴリズムは以下に示す通りです．

1. c = b - f(b) * (b - a) / (f(b) - f(a))

2. f(a) f(c) < 0 なら
   b = c，f(b) = f(c)
   そうでなければ
   a = c，f(a) = f(c)

3. |b - a| < ε ならば終了する．そうでなければ，1 に戻る．

３．代数方程式と行列の固有値・固有ベクトル

３．１ ベアストウ法

C/C++によるプログラム例　→　

JavaScript 版では，任意の実係数 n 次代数方程式の根を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「代数方程式（ベアストウ法）」をご覧ください．

　　実係数 n 次代数方程式，

f(x) = a₀xⁿ + a₁x^n-1 + ･･･ + a_n-1x + a_n = 0

のすべての根を求める方法としてベアストウ法があります．ベアストウ法は，対象とする式を，2 次式，

x² + px + q

と (n - 2) 次式の積の形に変換することを繰り返して解く方法です．p と q の値を決めるために，その初期値 p₀ と q₀ を与え，f(x) を x² + p₀x + q₀ で割った余りが 0 になるように，p₀ と q₀ を徐々に修正していきます．具体的なアルゴリズムは，以下に示す通りです．

1. p₀， q₀ を与え，k = 1 とおく

2. b_i = a_i - p_k-1b_i-1 - q_k-1b_i-2,　　　i = 0, 1, ･･･, n，　　b_-1 = b_-2 = 0

3. c_i = b_i - p_k-1c_i-1 - q_k-1c_i-2,　　　i = 0, 1, ･･･, n，　　c_-1 = c_-2 = 0

4. D = c_n-2² - c_n-3(c_n-1 - b_n-1)
   Δp = (b_n-1c_n-2 - b_nc_n-3) / D
   Δq = (b_nc_n-2 - b_n-1(c_n-1 - b_n-1)) / D

5. もし，|Δp| < ε， かつ， |Δq| < ε であれば，

   1. 2 次方程式 x² + p_k-1x + q_k-1 = 0 を解く

   2. b₀, ･･･, b_n-2 を，新たに，a₀, ･･･, a_n-2 とおき，かつ，n = n - 2 とし，1 へ戻る．ただし，n が 1 または 2 の場合は，その方程式を解く．
   そうでなければ，

   1. p_k = p_k-1 + Δp
      q_k = q_k-1 + Δq

   2. k = k + 1 とし，2 へ戻る．

３．２ 行列の固有値（フレーム法＋ベアストウ法）

C/C++によるプログラム例　→　

JavaScript 版では，任意の行列の固有値を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「行列の固有値（フレーム法＋ベアストウ法）」をご覧ください．

　　行列 A の固有ベクトルを x，固有値を λ とすると，

Ax = λx

という関係が成立します．この方程式が零ベクトル以外の解をもつための必要十分条件は，

|A - λI| = 0

となることであり，この方程式を A の特性方程式（固有方程式）といいます．そして，この方程式の n 個の根 λ₁，λ₂，･･･，λ_n は，A の固有値になっています．

　　従って，固有値を求めることは，この特性方程式を解くことになります．特性方程式は，

|A - λI| = λⁿ + b₁λ^n-1 + ･･･ + b_n-1λ + b_n = 0

と書き表せます．b₁ から b_n の値が決まれば，ベアストウ法によって上式の根を求めることができます．b₁ から b_n をフレーム法で求め，ベアストウ法で特性方程式の根を求めるといった方法で固有値を求めるのが以下に示すアルゴリズムです．

1. b₁ = -trA とする（「tr」はトレースを表し，対角要素の和である）

2. H_k-1 = AH_k-2 + b_k-1I
   b_k = -tr(AH_k-1) / k　　　k = 2, ･･･ n，　ただし，H₀ = I

3. ベアストウ法で固有値を求める．

３．３ 実対称行列の固有値・固有ベクトル（ヤコビ法）

C/C++によるプログラム例　→　

JavaScript 版では，任意の実対称行列の固有値・固有ベクトルを画面上で求めることができます．各固有値に対応する固有ベクトルは，各列に表示されます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「実対称行列の固有値・固有ベクトル（ヤコビ法）」をご覧ください．

　　n 次の実対称行列（要素がすべて実数である対称行列であり，固有値はすべて実数となる） A の固有ベクトルを x_i，固有値を λ_i とすると，

Ax_i = λ_ix_i　　　i = 1, 2, ･･･, n

という関係が成立します．今，

R = [x₁, x₂, ･･･, x_n]

とし，各 x_i が正規直行系をなしていれば，

とすると，

R^-1AR = R^TAR = Λ

という関係が成立します．従って，直交行列 R を求めれば，固有値と固有ベクトルが求まることになります．

　　直交行列 R を求めるために，まず，行列 A の非対角要素の内，絶対値が最大になる要素を 0 にするような直交行列 R_k を順次作成していき，最終的に R を求めます．つまり，

A₁ = R₁^TAR₁

A₂ = R₂^TA₁R₂ = R₂^TR₁^TAR₁R₂

　　　　　・・・

A_k = (R₁R₂･･･R_k)^TA(R₁R₂･･･R_k)

と計算していき，もし，A_k が対角行列になっていれば，求める R は，R₁R₂･･･R_k となります．

　　ヤコビ法の具体的アルゴリズムは，以下のようになります．

1. k = 1， A₀ = A， X₀ = I とおく．

2. 行列 A_k-1 の非対角要素の内，絶対値が最大になる要素 a_pq を見つける．

3. もし，|すべての非対角要素| < ε ならば，
   1. 終了する（A_k-1 の対角要素が固有値で，かつ，X_k-1 の各列が対応する固有ベクトル）
   そうでなければ，

   1. 要素 a_pq を 0 にするような直交変換
      A_k = R_k^TA_k-1R_k
      を行う．このとき，A_k の各要素の値は，以下のようになる．

      s = -a_pq
      t = 0.5(a_pp - a_qq)
      v = |t| / (s² + t²)^0.5
      sinθ = (0.5(1 - v))^0.5･sign(st)
      cosθ = (1 - sin²θ)^0.5
      a_pj^(k) = a_pj^(k-1)cosθ - a_qj^(k-1)sinθ
      a_qj^(k) = a_qj^(k-1)cosθ + a_pj^(k-1)sinθ
      a_ip^(k) = a_ip^(k-1)cosθ - a_iq^(k-1)sinθ
      a_iq^(k) = a_iq^(k-1)cosθ + a_ip^(k-1)sinθ
      a_ij^(k) = a_ij^(k-1)　　　以上において， i,j ≠ p,q
      a_pp^(k) = a_pp^(k-1)cos²θ + a_qq^(k-1)sin²θ - 2a_pq^(k-1)sinθcosθ
      a_qq^(k) = a_pp^(k-1)sin²θ + a_qq^(k-1)cos²θ + 2a_pq^(k-1)sinθcosθ
      a_pq^(k) = 0
      a_qp^(k) = 0

   2. X_k を，
      X_k = X_k-1R_k
      として計算する．このとき，X_k の各要素の値は，以下のようになる．

      x_jp^(k) = x_jp^(k-1)cosθ - x_jp^(k-1)sinθ
      x_jq^(k) = x_jq^(k-1)cosθ + x_jq^(k-1)sinθ　　　j = 1, 2, ･･･, n

   3. 2 へ戻る．

３．４ 最大固有値と固有ベクトル（べき乗法）

C/C++によるプログラム例　→　

JavaScript 版では，任意の行列の最大固有値と固有ベクトルを画面上で求めることができます．適当にパラメータを変更することによって，すべての固有値及び固有ベクトルを求めることも可能です．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「最大固有値と固有ベクトル（べき乗法）」をご覧ください．

　　べき乗法は，任意の初期ベクトル v₀ から始め，

v_k = Av_k-1 / ∥Av_k-1∥　　　k = 0, 1, 2, ･･･

という手続きを繰り返すと，∥Av_k-1∥，及び，v_k が，行列 A の最大固有値の絶対値 ｜λ｜，及び，その対応する固有ベクトル v に収束することを利用した方法です（初期ベクトルの与え方によっては，必ずしも最大固有値に収束しない）．最大固有値から，順に，複数の固有値，固有ベクトルを求めることが可能です．具体的アルゴリズムは，以下のようになります．

　　なお，この方法は，固有値が 0 の場合や，重複固有値がある場合に対しては適用できません．また，A^-1 の固有値は，A の固有値の逆数になりますから，最小固有値を求める方法としても利用できます（もちろん，逆行列が存在する場合に限ります）．

1. v₀ を与え，B = I とする．

2. l₀ = ∥v₀∥，k = 0 とする．

3. v_k = Bv_k / ∥Bv_k∥　　（丸め誤差を取り除くためであり，必ずしも毎回行わなくても良い）

4. l_k+1 = ∥Av_k∥,　　v_k+1 = Av_k / l_k+1

5. もし，|(l_k+1 - l_k) / l_k| < ε ならば，

   1. v_k+1 の要素の内，0 でないものを見つける．

   2. 対応する v_k の要素の符号が，v_k+1 のものと異なっていれば，l_k+1 = -l_k+1 とする．

   3. 固有値及び固有ベクトルとして，l_k+1 及び v_k+1 を記憶する．

   4. B = (A - l_k+1I)B, 　v₀ = Bv₀ として，2 へ戻る（次の固有値，固有ベクトルを求める手続き）．
   そうでなければ，

   1. k = k + 1 として，3 へ戻る．

４．数値微分

　　数値微分は，微分の定義に従い，以下のような形で計算します．

５．数値積分

５．１ 台形則

C/C++によるプログラム例　→　

JavaScript 版では，JavaScript の仕様に適合した形で積分したい式を入力することによって，任意の関数の積分を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「数値積分（台形則）」をご覧ください．

　　台形則では，積分区間 [a, b] を n 等分し，上図に示すように，台形の面積の和で近似して計算します．つまり，以下の式を計算することになります．

　　h = (b - a) / n, 　x_i = a + ih

５．２ シンプソン則

C/C++によるプログラム例　→　

JavaScript 版では，JavaScript の仕様に適合した形で積分したい式を入力することによって，任意の関数の積分を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「数値積分（シンプソン則）」をご覧ください．

　　シンプソン則による積分方法は以下のようになります．積分区間 [a, b] を 2n 等分し，

h = (b - a) / 2n, 　x_i = a + ih

としたとき，たとえば，3 点，

(x₀， f(x₀))， (x₁， f(x₁)), (x₂, f(x₂))

用いて，f(x) を 3 点を通る 2 次式 g(x) で近似すると，ラグランジュ補間法によって，以下のようになります．

　　この g(x) の積分によって，区間 [x₀, x₂] における f(x) の積分を近似すると以下のようになります．

以上より，区間 [a, b] の積分は，以下の式によって近似することができます．

６．常微分方程式

６．１ ルンゲ・クッタ法

C/C++によるプログラム例　→　

JavaScript 版では，JavaScript の仕様に適合した形で微分方程式を入力することによって，任意の微分方程式の解を画面上で求めることができます．具体的には，1 階の n 元連立微分方程式，

　　

の右辺を，変数には配列を使用して入力することになります．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「微分方程式（ルンゲ・クッタ）」をご覧ください．

　　ルンゲ・クッタ法について説明する前に，オイラー法によって微分方程式を解く基本的な考え方について説明します．微分方程式，

が与えられたとします．微分の定義によって，以下のような近似式が得られます．

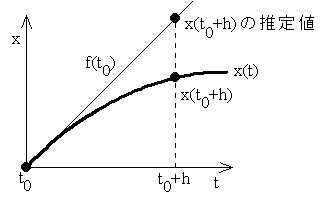
　　オイラー法では，この式に従って微分方程式を解いていきます．まず，初期値 t₀，x(t₀) (= x₀) を与えます．すると，与えられた微分方程式から，t₀ における接線の傾き f(t₀) を計算できます（下図参照）．これらのデータから，t₀+h における x(t₀+h) の推定値を計算します．

　　以下，t₀+h を 新たに t₀ と考え，この手続きを繰り返していきます．図からも明らかなように，h が大きいと，真の x(t₀+h) とその推定値の間には大きな差がありますが，h を十分小さくとることによって，この差を小さくすることができます．

　　オイラー法では，t₀ における傾き f(t₀) だけを利用して，x(t₀+h) を推定していますが，ルンゲ・クッタ法では，以下に示すように，複数点における傾きを利用しています．

g₁ = hf(t₀, x₀)

g₂ = hf(t₀ + h / 2, x₀ + g₁ / 2)

g₃ = hf(t₀ + h / 2, x₀ + g₂ / 2)

g₄ = hf(t₀ + h, x₀ + g₃)

x(t₀+h) = x₀ + (g₁ + 2g₂ + 2g₃ + g₄) / 6

７．補間法

７．１ ラグランジュ補間法

C/C++によるプログラム例　→　

JavaScript 版では，任意のデータに対して，n 次補間多項式による計算結果を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「補間法（ラグランジュ）」をご覧ください．

　　ラグランジュ補間法は，(n+1) 個の点 (x_i, y_i) (i = 0, 1, ･･･, n) が与えられたとき，与えられた点を通る n 次多項式，

f(x) = a₀xⁿ + a₁x^n-1 + ･･･ + a_n-1x + a_n

によって，補間する方法です．x が与えられたとき，f(x) は以下の式によって計算されます．

７．２ スプライン補間法

C/C++によるプログラム例　→　

JavaScript 版では，任意のデータに対して，スプライン補間法による計算結果を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「補間法（スプライン）」をご覧ください．

　　スプライン補間法は，与えられた点を通るなるべくなめらかな曲線によって，補間しようとするものです．具体的には，以下のような多項式によって補間します．

• 各区間を，最大次数が m （ここでは，m = 3 とします）である以下に示す多項式（ 3 次のスプライン関数）で近似します．
  z_i(x) = p_i + q_i(x - x_i) + r_i(x - x_i)² + s_i(x - x_i)³　　　i = 0,1,･･･,n-1

• 与えられた点を通り，かつ，1 階から m 階までの微係数の値が各点ですべて一致するように（つまり，z_i^(k)(x_i+1) = z_i+1^(k)(x_i+1)， k = 1, 2, 3），p_i，q_i，r_i，及び，s_i を決めます（一般に，r₀ = r_n = 0 とする）．

　　具体的なアルゴリズムは以下のようになります．

1. ステップ 1
   h_i = x_i+1 - x_i　　　i = 0,･･･,n-1
   b_i = 2(h_i + h_i-1)　　　i = 1,･･･,n-1
   d_i = 3{(y_i+1 - y_i) / h_i - (y_i - y_i-1) / h_i-1}　　　i = 1,･･･,n-1

2. ステップ 2
   g₁ = h₁ / b₁
   g_i = h_i / (b_i - h_i-1g_i-1)　　　i = 2,･･･,n-2
   u₁ = d₁ / b₁
   u_i = (d_i - h_i-1u_i-1) / (b_i - h_i-1g_i-1)　　　i = 2,･･･,n-1

3. ステップ 3
   r_n-1 = u_n-1
   r_i = u_i - g_ir_i+1　　　i = n-2,･･･,1
   r₀ = 0

4. ステップ 4　　x_i < x < x_i+1 のとき
   p_i = y_i = f(x_i)
   q_i = (y_i+1 - y_i) / h_i - h_i(r_i+1 + 2r_i) / 3
   s_i = (r_i+1 - r_i) / 3h_i
   y = p_i + q_i(x - x_i) + r_i(x - x_i)² + s_i(x - x_i)³

７．３ ベジエ曲線

C/C++によるプログラム例　→　

JavaScript 版では，任意のデータに対して，ベジエ曲線上の座標を画面上に出力することができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「補間法（ベジエ曲線）」をご覧ください．

　　ここで述べるベジエ曲線は，先の節で述べたような補間法とは異なります．つまり，与えられた点を通る曲線を描くのではなく，与えられた点（B₀，B₁，・・・，B_n）で構成される定義多角形（ベジエ多角形）から，次式によって決まる曲線を描きます．

P(t) = ΣB_iJ_{n , i}(t)　　　0 ≦ t ≦ 1

ここで，P(t) は曲線上の点の座標であり，t = 0 の時は B₀ に，また，t = 1 の時は B_n に一致します．また，J_{n , i}(t) は，ベジエ基底関数と呼ばれ，以下の式で計算されます．

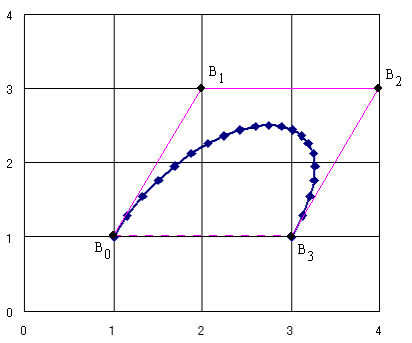
　　たとえば，n = 3 とし，ベジエ多角形を B₀ = (1 1)，B₁ = (2 3)，B₂ = (4 3)，B₃ = (3 1) とすると，ベジエ曲線は以下のようになります（プログラム例は，この曲線を描くためのものです）．

　　なお，ベジエ曲線には，以下のような性質があります．

• おおむね，定義多角形の形に従う

• 曲線の始点と終点は，定義多角形の最初と最後の点に一致する

• 曲線と始点と終点における接線ベクトルの方向は，定義多角形の最初と最後の辺の方向に一致する

• 曲線は，定義多角形の凸包の中に包含される

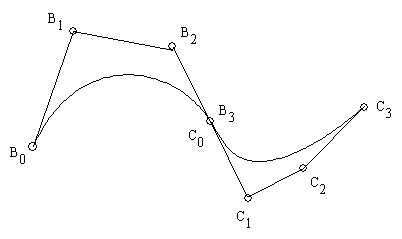
　　ベジエ曲線を複数個つなげて，下の図に示すような，複雑な曲線を描くこともできます．その際，接続点で，1 階の導関数が一致するためには，図に示すように，最初の定義多角形の最後の辺の方向と大きさが，2 番目の定義多角形の最初の辺の方向と大きさが一致していなければなりません（B₃ - B₂ = C₁ - C₀）．