
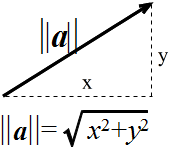
a + (ーa) = 0
 のような形で表現することも可能です.
のような形で表現することも可能です.
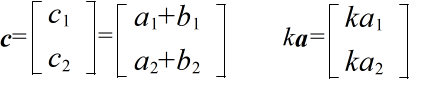
- [定義] 線形空間(ベクトル空間) 集合 V の任意の元 a,b に対して,それらの和及びスカラー倍が集合 V の元となり,かつ,それらが以下に示す性質を満たす時,V を実数全体の集合 R 上の線形空間(ベクトル空間)という.
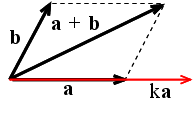
- (1) 結合則: (a + b) + c = a + (b + c)
- (2) 交換則: a + b = b + a
- (3) 0 ベクトルの存在: a + 0 = 0 + a = a を満たす元 0 がただ一つ存在する
- (4) 逆元の存在: a + x = x + a = 0 を満たす元 x = -a がただ一つ存在する
- (5) 1・a = a
- (6) k(a + b) = ka + kb k:実数
- (7) (m + n)a = ma + nb m,n:実数
- (8) (mn)a = m(n)a m,n:実数
- (1) 結合則: (a + b) + c = a + (b + c)
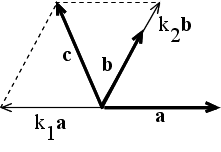
c = k1a + k2b
- [定義] 線形従属(一次従属)と線形独立(一次独立) n 個のベクトル ai ( i = 1, 2, ・・・, n )の線形結合(一次結合)が 0 となる式,
- c1a1 + c2a2 + ・・・ + cnan = 0
- において,同時には 0 でない実定数 ci が存在する場合(あるベクトルが,他のベクトルの線形結合で表現できる場合),n 個のベクトルは線形従属(一次従属)であるという.また,同時には 0 でない実定数 ci が存在しない場合,n 個のベクトルは線形独立(一次独立)であるという.
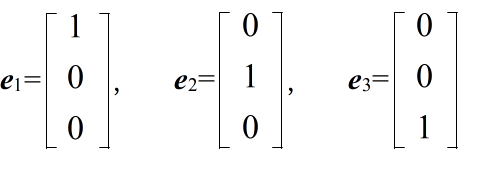
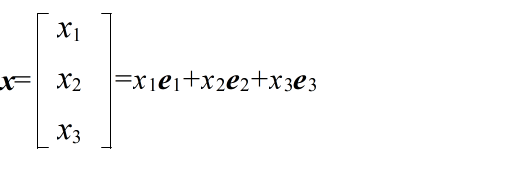
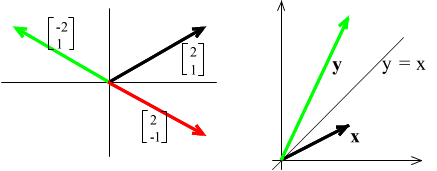
- [定義] 内積と外積 2 つのベクトル a,b が与えられ,それらのなす角を θ としたとき,ベクトル a,b の内積(スカラー積) a・b を以下のように定義する.
- a・b = ||a|| ||b|| cos θ = a1b1 + a2b2 + ・・・ + anbn
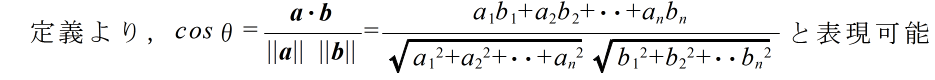
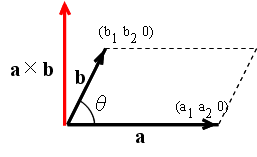
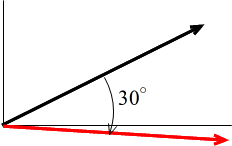
- また,外積(ベクトル積) a×b を以下のように定義する(右図の赤いベクトル).
- a×b = (||a|| ||b|| sin θ)e
- ただし,ベクトル e は,ベクトル a をベクトル b に重なるように回転したとき(θ < π),右ねじが進む方向に向かう単位ベクトルである(ベクトル a と b を含む平面に直交するベクトル).
a×b = [a2b3-a3b2 a3b1-a1b3 a1b2-a2b1]T
a×b = [0 0 a1b2-a2b1]T
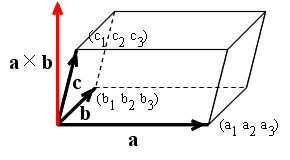
c・(a×b)
a1b2c3 + a2b3c1 + a3b1c2 - a1b3c2 - a2b1c3 - a3b2c1
- [定義] 数値を以下に示すように,n 行 m 列の形に並べたものを,n 行 m 列行列( n×m 型行列)という.
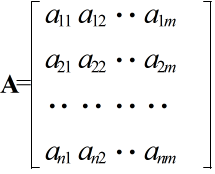
- ここで,aij を行列 A の (i,j) 要素,元,(i,j) 成分,i 行 j 列の成分等という.特に,1 行 m 列の行列を m 次の行ベクトル,また,n 行 1 列の行列を n 次の列ベクトル(単に,ベクトル)という.行列は,一般に,英大文字の太字で表現されます.
2x + y + z = 7 x + y - z = 2 3x + 2y - 2z = 5
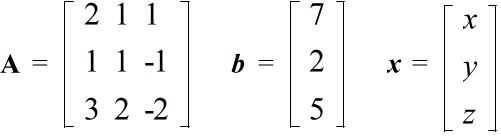
Ax = b
x = A-1b
- 0 行列 すべての要素が 0
- 実行列 aij が実数( aij は行列の i 行 j 列要素とする)
- 複素行列 aij が複素数
- 転置行列 B = AT ( bij = aji ) 行と列を入れ替えた(転置した)行列
- 正方行列 n 行 n 列の行列
- 主対角線 左上から右下に向かう対角線
- 対角成分 aii
- トレース( Trace ) tr A = Σ aii (対角成分の和)
- 対角行列 対角成分以外の成分がすべて 0 である行列
- 単位行列 対角成分が 1 である対角行列( I,または,E で表す)
- 三角行列
- 上三角行列 i > j に対し,aij = 0 である行列
- 下三角行列 i < j に対し,aij = 0 である行列
- 対称行列 A = AT
- 交代行列 A = -AT (対角成分はすべて 0)
- 直交行列 ATA = AAT = I
- 定数倍 各要素の値が定数倍されます.
- B = k A bij = k aij
- 加法と減法 同じ型の(行及び列の数が同じ)行列に対してだけ定義されます.
- 和 C = A + B cij = aij + bij
- 差 C = A - B cij = aij - bij
- 積 可換ではありません.つまり,AB と BA が定義できたとしても,一般的に,AB = BA とはなりません.なお,乗算の結果を確認したいような場合は,「ガウス-ジョルダンの消去法」を利用可能です.
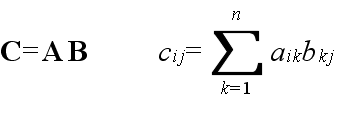
A: m × n, B: n × l のときだけ定義でき,結果 C は,m × l となる.
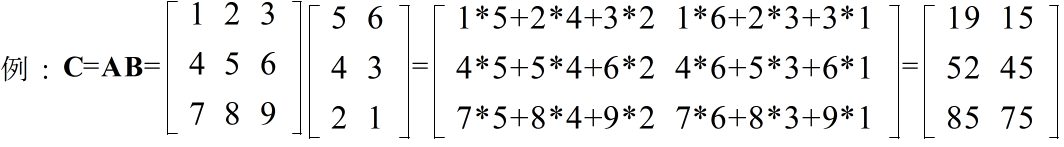
- 行列のべき乗
A0 = I, A1 = A, A2 = AA, A3 = A2A,・・・
- 行列演算の性質
- A + 0 = 0 + A = A
- A + (-A) = (-A) + A = A - A = 0
- (AB)C = A(BC)
- A(B + C) = AB + AC
- (A + B)C = AC + BC
- IA = AI = A
- 0A = A0 = 0
- AB ≠ BA
- a・b = aTb (内積)
- A + 0 = 0 + A = A
- [定義] 一つの順列において,2 要素の順序が,標準の順列における同じ 2 要素の順序と異なるときには,その 2 要素の間には一つの転位または転倒があるという.一つの順列において,転位をもつ 2 要素の組数をその順列の転位の数という.そして,偶数個の転位をもつ順列を偶順列,奇数個の転位をもつ順列を奇順列という.
- [定義] n × n ( n 次)の正方行列 A
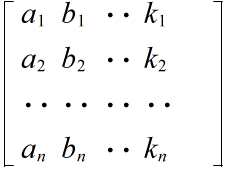
- の各行及び各列から必ず 1 個,そして,唯 1 個の要素を取って,これを a,b,・・・,k の順に並べて積を作ると,この積の中には,n 個の文字 a,b,・・・,k,及び,添え字 1,2,・・・,n は必ず一度,そして,唯一度ずつ現れる.その積は,aαbβ・・・kλ のような形をもち,αβ・・・λ は,1,2,・・・,n の一つの順列とみなすことができる.
- そこで,順列 αβ・・・λ が偶順列の時には,積 aαbβ・・・kλ に + をつけ,奇順列の時には - をつけて作ったすべての積( n! 個存在する)の和を作ると多項式が得られる.この多項式を,行列 A の行列式といい,以下のように表す.
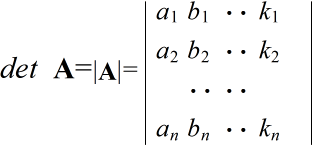
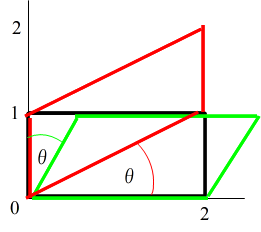
- 例2.1: n = 2 の場合,標準の順列 (1 2) に対し,積は,
- 偶順列 (1 2)
- 奇順列 (2 1)
- 奇順列 (2 1)
- であり,行列式は以下のようになります.

- = a1b2 - a2b1
- = a1b2 - a2b1
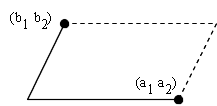
- 幾何学的には,右図に示す平行四辺形の面積を表しています.
- 例2.2: n = 3 の場合,標準の順列 (1 2 3) に対し,積は,
- 偶順列 (1 2 3), (2 3 1), (3 1 2)
- 奇順列 (1 3 2), (2 1 3), (3 2 1)
- 奇順列 (1 3 2), (2 1 3), (3 2 1)
- であり,行列式は以下のようになります.
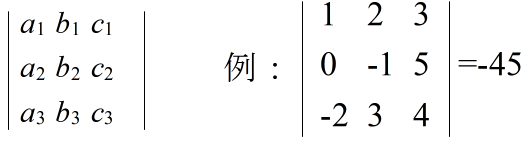
- = a1b2c3 + a2b3c1 + a3b1c2 - a1b3c2 - a2b1c3 - a3b2c1
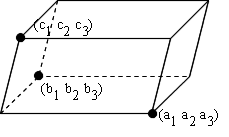
- 幾何学的には,右図に示す平行六面体の体積を表しています.
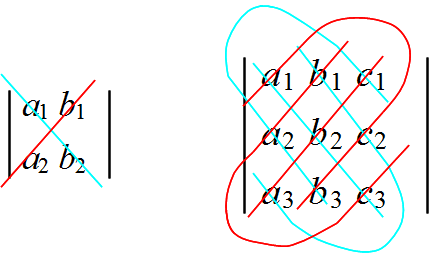
- 行と列を入れ換えても値は変わらない.
- 二つの行(列)を入れ換えると符号だけが変化する.
- ある行(列)のすべての要素が二つの数の和で表現できるときは,その行(列)の各要素を行(列)とし,他の行(列)の要素はすべて同じである二つの行列式の和として表現できる.
- ある行(列)を k 倍すると全体の値が k 倍になる.
- ある行(列)の各要素に他の行(列)の対応する要素の k 倍を掛けて加えても行列式の値は変わらない.
- ある行(列)のすべての要素の値が 0 の時は,行列式の値も 0 になる.
- 二つの行(列)の対応する要素が比例関係にあるときは,行列式の値は 0 になる.
- ある行(列)のすべての要素が,他のいくつかの行(列)の線形結合で表現可能なとき,例えば,列 k がそれ以外のいくつかの列の和,
ak = ciai + cjaj + ・・・ + cmam
として表現可能なとき,行列式の値は 0 になる.
- [定義] 行列式において,一つの要素を含む行と列を除いた残りの要素で作った行列式をその要素の小行列式という.たとえば,i 行 j 列要素の小行列式を Mij のように表す.また,
- Aij = (-1)i+jMij
- を,要素 (i,j) の余因数(余因子)という.
|A| = ar1Ar1 + ar2Ar2 + ・・・ + arnArn 第 r 行で展開 = (-1)r+1ar1Mr1 + (-1)r+2ar2Mr2 + ・・・ + (-1)r+narnMrn = a1sA1s + a2sA2s + ・・・ + ansAns 第 s 列で展開 = (-1)1+sa1sM1s + (-1)2+sa2sM2s + ・・・ + (-1)n+sansMns
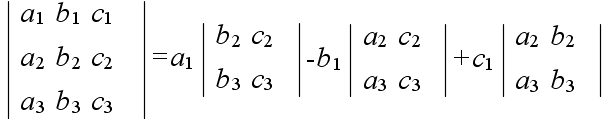
= a1b2c3 + a2b3c1 + a3b1c2 - a1b3c2 - a2b1c3 - a3b2c1
2x + y + z = 7 x + y - z = 2 3x + 2y - 2z = 5
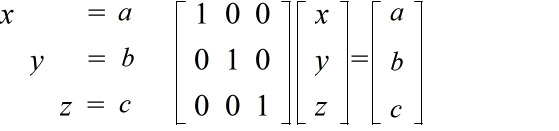
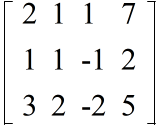
- 1 行目と 2 行目を入れ替える( 1 番目の式と 2 番目の式を入れ替える.以下同様)
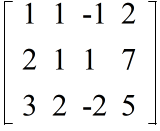
- 1 行目の 2 倍を 2 行目から引く
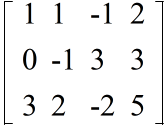
- 1 行目の 3 倍を 3 行目から引く
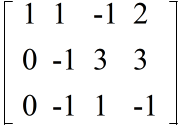
- 2 行目を -1 倍する
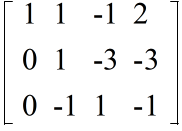
- 1 行目から 2 行目を引く
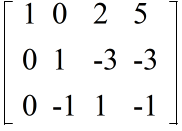
- 3 行目に 2 行目を加える
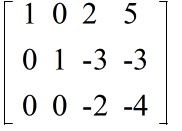
- 3 行目を -2 でわる
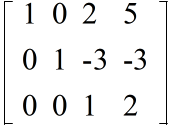
- 3 行目の 2 倍を 1 行目から引く
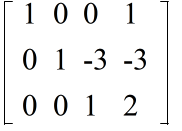
- 3 行目の 3 倍を 2 行目に加える
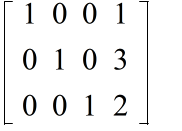
- |A| ≠ 0
- となる.
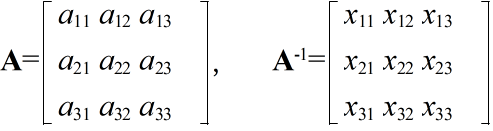
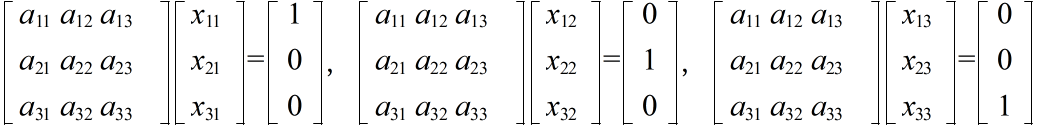
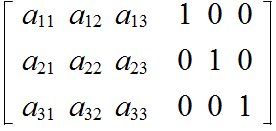
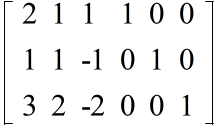
- 1 行目と 2 行目を入れ替える( 1 番目の式と 2 番目の式を入れ替える.以下同様)
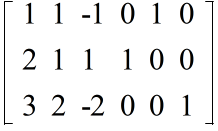
- 1 行目の 2 倍を 2 行目から引く
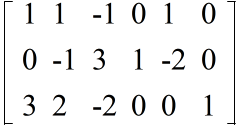
- 1 行目の 3 倍を 3 行目から引く
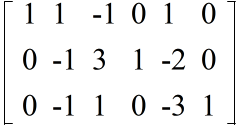
- 2 行目を -1 倍する
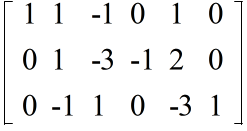
- 1 行目から 2 行目を引く
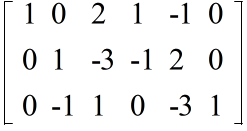
- 3 行目に 2 行目を加える
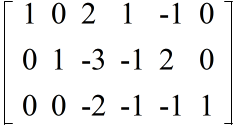
- 3 行目を -2 でわる
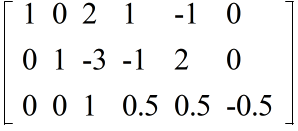
- 3 行目の 2 倍を 1 行目から引く
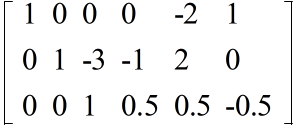
- 3 行目の 3 倍を 2 行目に加える
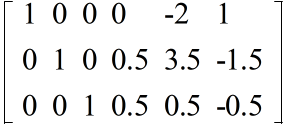
Ax = b
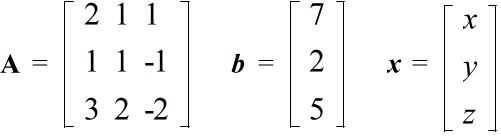
x = A-1b

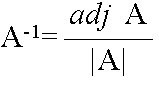
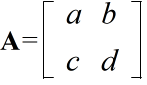
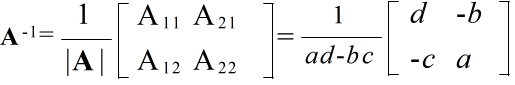
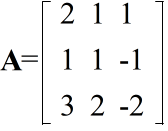
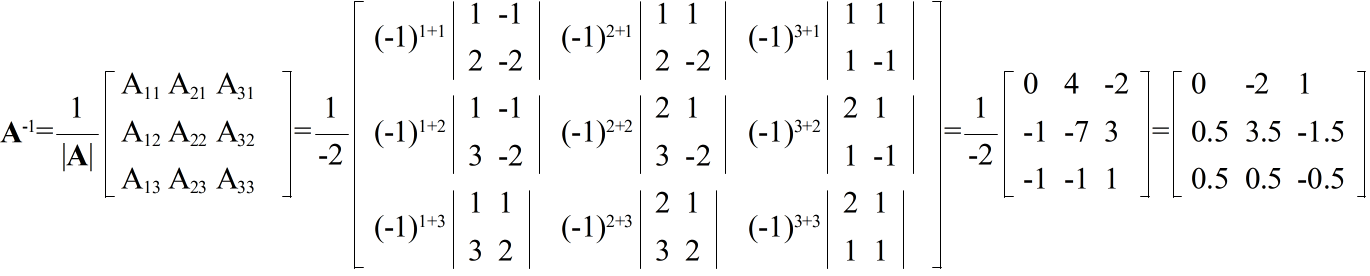
- [定義] n×m の行列 A から,任意に r 個の行と r 個の列をとって,その交わりの上にある要素をそのままとって作った r 次の行列式をAの r 次の小行列式という.r 次の小行列式の中には 0 でないものが少なくとも一つあって,(r+1) 次以上の小行列式はいずれも 0 であるとき,行列 A の階数(ランク,または,位)は r であるという.そして,A の階数を
- r = Rank A
- で表す.また,行列 A の階数は,行列 A の線形独立な列(行)ベクトルの数とも言える.従って,
- Rank A ≦ n, m
- という関係がある.
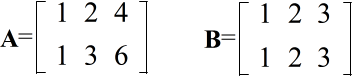
|A| ≠ 0 ⇔ Rank A = n
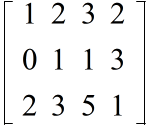
- 3 行目から 1 行目の 2 倍を引く
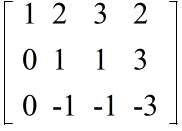
- 3 行目に 2 行目を加える
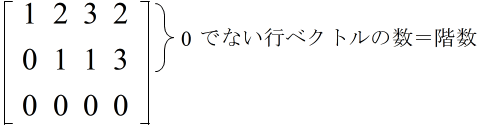
- [定義] 線形写像(線形変換) 集合 V,W が R 上の線形空間(ベクトル空間)であるとき,写像 f : V → W が,任意の a,b ∈ V,及び,k ∈ R に対して,以下の条件を満たす時,f を V から W への線形写像(線形変換)という.
- (1) f(a + b) = f(a) + f(b)
- (2) f(ka) = kf(a)
- (1) f(a + b) = f(a) + f(b)
f(V) = { f(x) | x ∈ V } y = f(x) = Ax ( x ∈ Rn,y ∈ Rm )
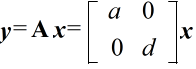
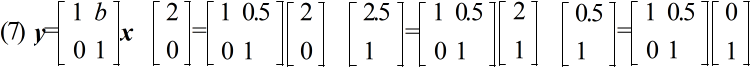
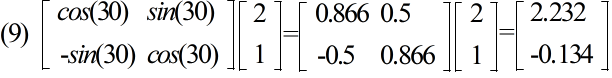
Ax + t
- 同一直線上にある 3 点は,アフィン変換後も同一直線上にある.
- 同一直線上にある 3 点 A,B,C に対して,AB : BC の比が変化しない.
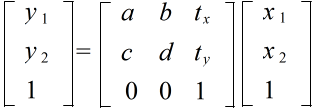
Java における AffineTransform クラス,AffineTransformOp クラス
JavaScript おける transform メソッド
- [定義] n 次の正方行列 A に対して,0 でないベクトル x があって,
- Ax = λx
- が成り立つとき( x ≠ 0 の解をもつとき),λ を A の固有値,x を固有ベクトル(一般的に,一意には決まらない.固有ベクトルをスカラー倍したものも固有ベクトルになる)という.したがって,固有値は,
- |A - λI| = 0 (固有方程式,又は,特性方程式という)
- の根となる.
- 固有値はすべて実数である.
- 二つの異なる固有値に対する固有ベクトルは直交する.
- ベクトルの直交: 2 つのベクトルの内積が 0 ( 2 つのベクトルのなす角が 90 度)
- 適当な直交行列 L によって,LTAL が対角行列になるようにすることができる.
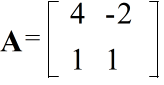
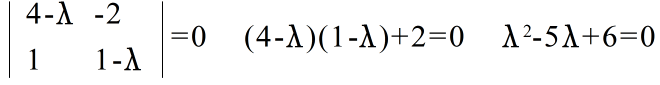
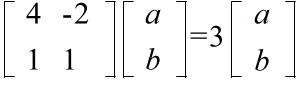
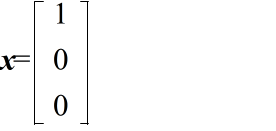
a - 2b = 0 a - 2b = 0
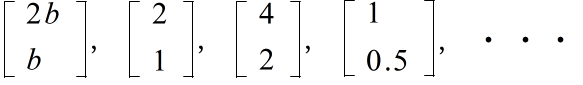
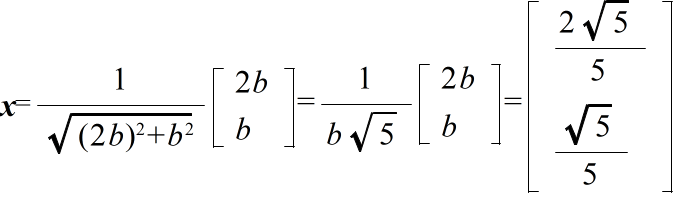
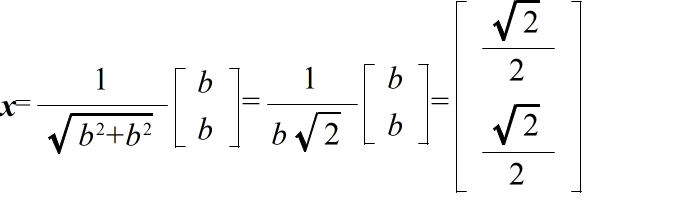
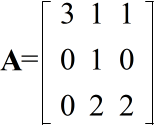
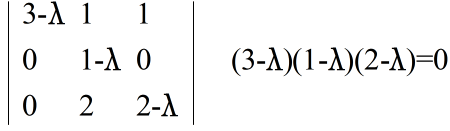
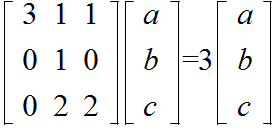
3a + b + c = 3a b = 3b 2b + 2c = 3c
3a + b + c = 2a b = 2b 2b + 2c = 2c
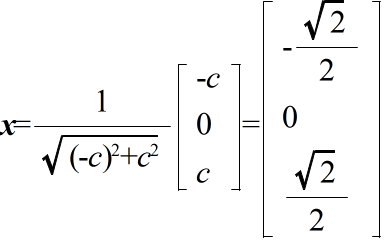
3a + b + c = a b = b 2b + 2c = c
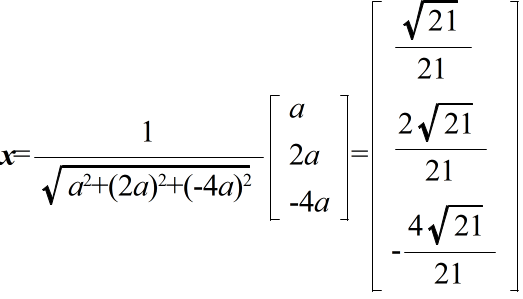
- [定理] n 次の正方行列 A が n 個の異なる固有値 λ1,λ2,・・・,λn を持ち,それぞれの固有値に対する固有ベクトルが x1,x2,・・・,xn であったとする.このとき,これら n 個のベクトルを列に持つ行列 P = [x1,x2,・・・,xn]によって,行列 A を以下に示すように対角行列に変換することができる.
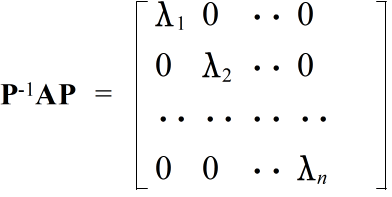

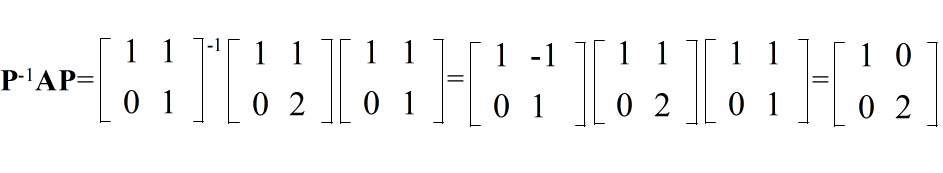

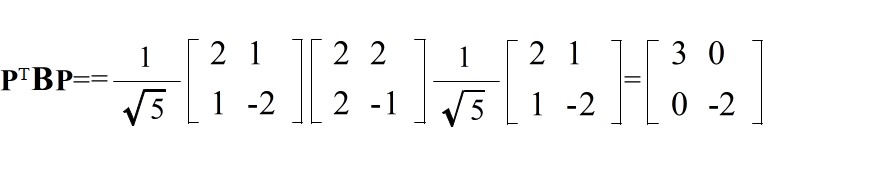
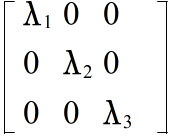
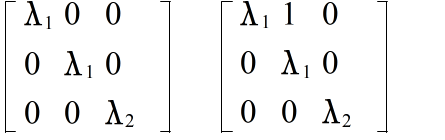
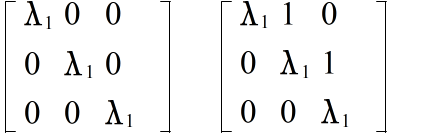
- [定義] n 次の実対称行列 A と n 次元ベクトル x に対して,
- QA(x) = xTAx = ΣΣaijxixj
- を行列 A に対する二次形式という.すべての x に対して,二次形式が非負であるとき,つまり,
- xTAx ≧ 0, ∀x ∈ Rn
- のとき,A は半正定値( positive semidefinite ),あるは,非負定値( nonnegative definite )であるという.また,すべての x≠0 に対して二次形式が正であるとき,つまり,
- xTAx > 0, ∀x≠0 ∈ Rn
- のとき,A は正定値( positive definite )であるという.正定値,及び,半正定値は,行列 A のすべての固有値が 0 より大きい,及び,0 以上であるということに対応する.
xTAx = a11x2 + 2 a12xy + a22y2 = c > 0, ただし,x = [x y]T


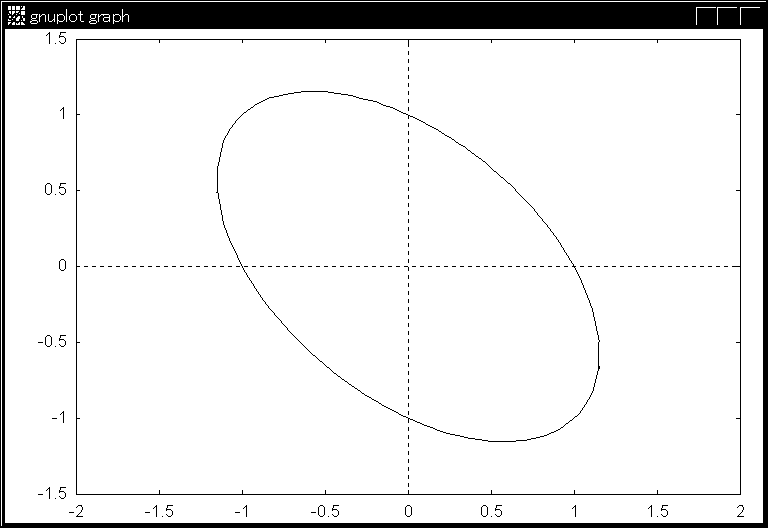

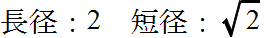
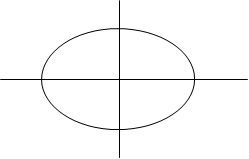
x2 + 2y2 = 1
x'TAx' = (Px)TAPx = xTPTAPx = 1
| 情報学部 | 菅沼ホーム | SE目次 | 索引 |
