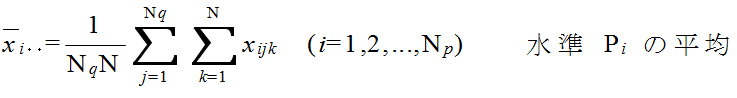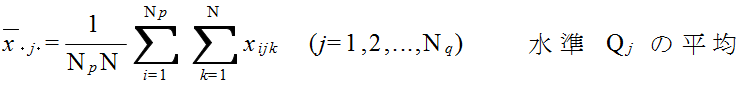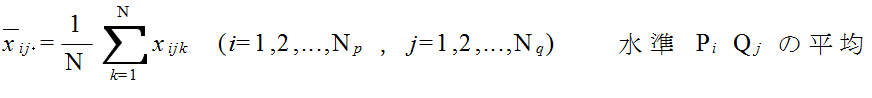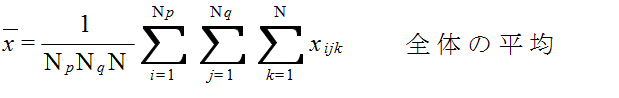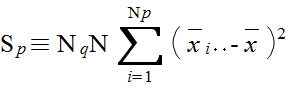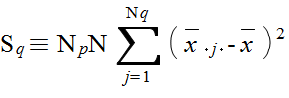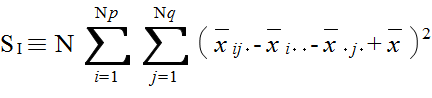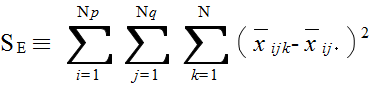- 量的データ: 数量(数値)で表されるもの(「気温」,「所得」,「身長」,・・・)
- 間隔尺度: 差が計れる,つまり,測定単位が存在する(例:摂氏温度).
- 比率尺度(比例尺度): 間隔尺度の中で,測定単位と絶対原点がある(例:長さ,重さ).
- 質的データ: 数量で表されないデータ(「好き,嫌い」,「買う,買わない」,「国籍」,・・・)
- 名義尺度: 同等関係がわかる.つまり,等しいものには同じ数字を与え,違ったものには違った数字を与えるといった方式でデータを扱う.与えられた数字の大小には意味がない.
- 順序尺度: より上位のものには大きな数字を,下位のものには小さな数字を与えるといった方式でデータを扱う(ただし,差には意味がない).たとえば,「嫌い」,「普通」,「好き」に,各々,0,1,2 を与えるといった方法である.
| 基準変数 (目的変数) | 多変量解析の目的 | 説明変数 | ||
|---|---|---|---|---|
| 量的 | 質的 | |||
| あり | 量的 | ・予測式(関係式)の発見 ・量の推定 | ・重回帰分析 ・正準相関分析 | ・数量化分析Ⅰ類 |
| 質的 | ・標本の分類 ・質の推定 | ・クラスター分析 ・判別分析 | ・クラスター分析 ・数量化分析Ⅱ類 | |
| なし | ・多変量の統合整理(減らす) ・変量の分類 ・代表変量の発見 | ・主成分分析 ・因子分析 | ・数量化分析Ⅲ,Ⅳ類 | |
(yi, xi1, xi2, ・・・, xin) i = 1, 2, ・・・, N
y = b0 + b1x1 + b2x2 + ・・・ + bnxn
s = [y - Xb]T[y - Xb]
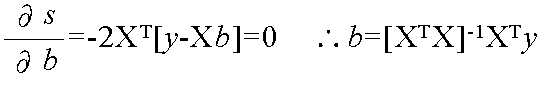
y = [y1 y2 ・・・ yN]T
b = [b0 b1 b2 ・・・ bn]T
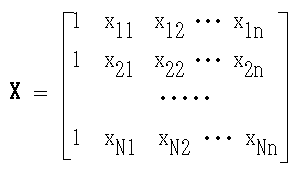
- 例1 : 偏回帰係数を計算するための C/C++ によるプログラム例 →
 JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「重回帰分析」をご覧ください.
JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「重回帰分析」をご覧ください.
- このプログラムに対して,説明変数の数(n)とデータの数(N)を与え,続いて,N 組のデータ(最初が,目的変数の値)を与えれば,偏回帰係数を計算できます.プログラム例に添付したデータに対して,偏回帰係数は以下のようになります.
b0 46.592245 b1 0.015153 b2 0.436445 b3 -0.389181
- x = [y, x1, x2, x3] としたとき,この例で使用したデータの平均値,及び,相関行列 R は,
- x の平均値 = [49.56 47.49 49.13 49.32]

- のようになっています.相関行列からも明らかなように,y と,x2 及び x3 との間に強い相関があります.そして,その結果が,偏回帰係数にも現れています.
x1, x2, ・・・, xq
r 個の変数の組: x1, x2, ・・・, xr s(= q - r ≧ r)個の変数の組: xr+1, xr+2, ・・・, xr+s
y = a1x1 + a2x2 + ・・・ + arxr z = b1xr+1 + b2xr+2 + ・・・ + bsxr+s
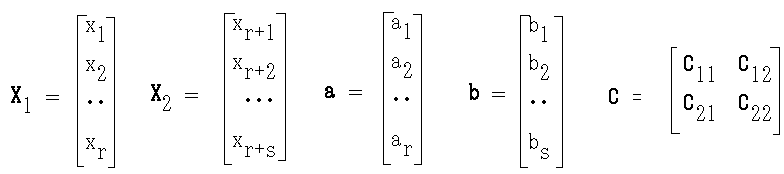
E[X1] = E[X2] = 0, V[y] = aTC11a = 1, V[z] = bTC22b = 1
ryz = aTC12b
f = aTC12b - 0.5 λ (aTC11a - 1) - 0.5 μ (bTC22b - 1)
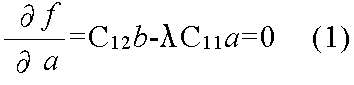
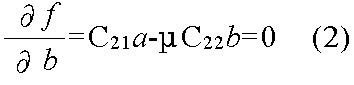
μ C12b - λμ C11a = 0 C12C22-1C21a - μ C12C22-1C22b = 0 ∴ C12C22-1C21a - μ C12b = 0
C12C22-1C21a - λμ C11a = 0
(C11-1C12C22-1C21a - λμ I) a = 0
aTC12b - λ aTC11a = 0 ∴ aTC12b = ryz = λ
aTC12b - μ bTC22b = 0 ∴ aTC12b = ryz = μ
b = C22-1C21 a / λ
(C11-1C12C22-1C21 - λ2 I) a = 0 ただし,aTC11a = 1 λ2 は,C11-1C12C22-1C21 の固有値であり,a は,対応する固有ベクトル b = C22-1C21 a / λ ただし,bTC22b = 1 ryz = λ
- 例2 : 正準相関分析を行うための C/C++ によるプログラム例 →
 JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「正準相関分析」をご覧ください.
JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「正準相関分析」をご覧ください.
- このプログラムに対して,各組の変数の数(r と s, r ≦ s)とデータの数(n)を与え,続いて,n 組のデータを与えれば,正準相関分析を実行できます.例1 と同じデータ(ただし,y を x1,x1 を x2,x2 を x3,x3 を x4 と読み替える)を使用して,正準相関分析を行ってみます.
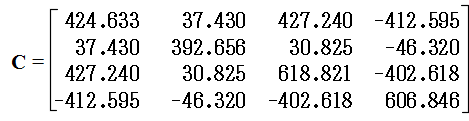
- 最初に,x1 と(x2, x3, x4)の組に対して正準相関分析を行うと以下のようになります.x1 と x3,及び,x4 の間に強い相関があるため,x3,及び,x4 に対する係数が大きくなっています.また,相関係数は,その定義より,必ず,各変数間の相関係数より大きな値になります.正準相関分析では,各データの平均値を 0 としていますので,重回帰分析における b0 に対応する部分がありませんが,基本的に,重回帰分析と同様の結果が得られています.なお,分散共分散行列 C は右のようになっています.
- このプログラムに対して,各組の変数の数(r と s, r ≦ s)とデータの数(n)を与え,続いて,n 組のデータを与えれば,正準相関分析を実行できます.例1 と同じデータ(ただし,y を x1,x1 を x2,x2 を x3,x3 を x4 と読み替える)を使用して,正準相関分析を行ってみます.
相関係数 0.904770 a 0.048528 b 0.000813 0.023409 -0.020874
- 次に,(x1, x2) と (x3, x4) に対して,正準相関分析を行うと以下のようになります.第 1 正準相関係数(0.904657)に対応する部分を見ると,データ間の相関から予想したような結果が得られています.第 2 正準相関係数は,第 1 正準相関係数に比較して非常に小さな値となっており,余り意味のないものとなっています.
相関係数 0.904657 a 0.048516 0.000138 b 0.023406 -0.020945 相関係数 0.041613 a -0.004599 0.050679 b -0.047911 -0.049606
変量: x1, x2, ・・・, xp N 個のデータ: x1i, x2i, ・・・, xpi i = 1, 2, ・・・, N
z = a1x1 + a2x2 + ・・・ + apxp = aTx ただし,a = [a1 a2 ・・・ ap]T, x = [x1 x2 ・・・ xp]T
z1 = a11x1 + a12x2 + ・・・ + a1pxp
z2 = a21x1 + a22x2 + ・・・ + a2pxp
V[z] = V[aTx] = aT V[x] a = aT C a
(xi - μ) / σ
v = aTCa - λ (aTa - 1)
Ca - λa = 0 ∴|C - λI| = 0
aTCa - λaTa = 0 ∴aTCa = λ
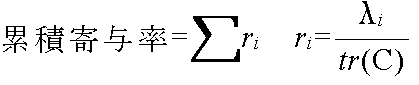

- 例3 : 主成分分析を行うためのC/C++ によるプログラム例(→
 JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「主成分分析」をご覧ください.
JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「主成分分析」をご覧ください.
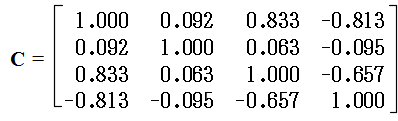
- このプログラムに対して,変数の数(p)とデータの数(n)を与え,続いて,n 組のデータを与えれば主成分分析を実行できます.再び,例1 と同じデータ(ただし,y を x1,x1 を x2,x2 を x3,x3 を x4 と読み替える)を使用します.主成分分析を行うと,以下に示すような結果になります(第 1 主成分から順には並べてありません).なお,分散共分散行列 C は右のようになっています.
主成分 0.118306 係数 0.796646 -0.008174 -0.462969 0.388520 主成分 0.987518 係数 -0.050663 0.995047 -0.080488 0.028908 主成分 2.551440 係数 0.601096 0.092426 0.563442 -0.559172 主成分 0.342736 係数 0.038354 0.035656 0.679496 0.731808
- この結果の第 1 主成分(2.551440)を見ますと,互いに相関が強い変量 x1, x3, 及び, x4から構成され,また,第 2 主成分は,それらの変量と相関が少ない変量 x2 からなっているのがよく分かります.
変量: x = [x1 x2 ・・・ xp]T N 個のデータ: x1i, x2i, ・・・, xpi i = 1, 2, ・・・, N
x = Af + e
f = [f1 f2 ・・・ fm]T e = [e1 e2 ・・・ ep]T 特殊因子(誤差)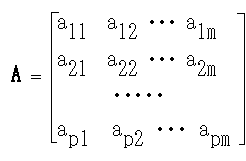
[a1i a2i ・・・ api]T i = 1, 2, ・・・, m
C = V[x] = V[Af + e] = A V[f] AT + V[e] = AAT + E = R + E
R = AAThi = Σj aij2 共通性と呼ぶ
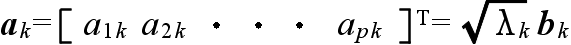
- hi を適当な値に初期設定する.
- R から因子負荷量を計算する.因子負荷量の計算には,R の固有値の大きい方から順に m 個の固有値と固有ベクトルを利用する.
- 因子負荷量から共通性を計算する.もし,|新たに計算した共通性 - 前回の共通性| < ε であれば,
- 終了.
- そうでなければ,
- R の対角要素を,新たに計算した共通性で置き換えて,2 へ戻る.
- 例4 : 因子分析を行うためのC/C++ によるプログラム例 →
 JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「因子分析」をご覧ください.
JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「因子分析」をご覧ください.
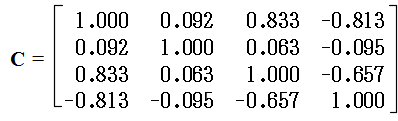
- このプログラムに対して,共通因子負荷量の数(m),変数の数(p),及び,データの数(n)を与え,続いて,n 組のデータを与えれば因子分析を実行できます.再び,例1 と同じデータ(ただし,y を x1,x1 を x2,x2 を x3,x3 を x4 と読み替える)を使用します.因子分析を行うと,以下に示すような結果になります.主成分分析の結果と非常によく似た結果が得られています.なお,分散共分散行列 C は右のようになっています.
固有値 2.360858 共通因子負荷量 1.012595 0.161506 0.818013 -0.800175 固有値 0.984701 共通因子負荷量 -0.072858 0.986512 -0.070533 0.034812
P(1|1) = ∫G1f1(x)dx : 集団 1 に属するものが,集団 1 に属すると正しく判断される確率 P(2|2) = ∫G2f2(x)dx : 集団 2 に属するものが,集団 2 に属すると正しく判断される確率 P(2|1) = ∫G2f1(x)dx : 集団 1 に属するデータが,集団 2 に属すると判断される確率 P(1|2) = ∫G1f2(x)dx : 集団 2 に属するデータが,集団 1 に属すると判断される確率
C(2|1) > 0 : 集団 1 に属するにもかかわらず,集団 2 に属すると判断されたときの損失 C(1|2) > 0 : 集団 2 に属するにもかかわらず,集団 1 に属すると判断されたときの損失
C(2|1)・P(1)・P(2|1) + C(1|2)・P(2)・P(1|2) = C(2|1)・P(1)∫G2f1(x)dx + C(1|2)・P(2)∫G1f2(x)dx = ∫G2(C(2|1)・P(1)f1(x) - C(1|2)・P(2)f2(x))dx + C(1|2)・P(2)∫Sf2(x)dx = ∫G1(C(1|2)・P(2)f2(x) - C(2|1)・P(1)f1(x))dx + C(2|1)・P(1)∫Sf1(x)dx S は,標本空間全体
C(1|2)・P(2)f2(x) = C(2|1)・P(1)f1(x)
C(1|2)・P(2)f2(x) ≦ C(2|1)・P(1)f1(x) : 集団 1 に属していると判断 C(1|2)・P(2)f2(x) > C(2|1)・P(1)f1(x) : 集団 2 に属していると判断
d2 = (x - y)T C-1 (x - y) C:分散共分散行列
x = [x1 x2 ・・・ xn]T y = [y1 y2 ・・・ yn]T
- 連続量で表されるデータ
- ユークリッド距離 d2 = Σ (xi - yi)2
- 重み付きユークリッド距離 d2 = Σ wi (xi - yi)2
- マハラノビスの距離 d2 = (x - y)T C-1 (x - y) C: 分散共分散行列
- 内積による類似度 sxy = xT y
- ユークリッド距離 d2 = Σ (xi - yi)2
- カテゴリーデータ(各変量の値が 0 または 1 )
- 以下の説明における変数の意味:
- a = Σ xkyk データ x と y において,共に 1 となる変量の個数
- b = Σ xk(1 - yk) データ xで 1,データ y で 0 となる変量の個数
- c = Σ (1 - xk)yk データ x で 0,データ y で 1 となる変量の個数
- d = Σ (1 - xk)(1 - yk) データ x と y において,共に 0 となる変量の個数
- → n = a + b + c + d
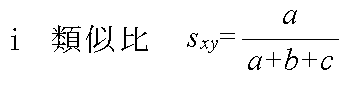

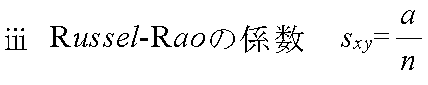
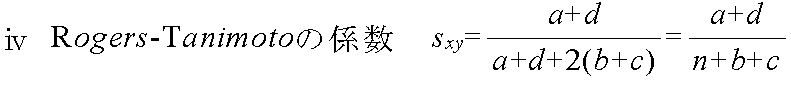

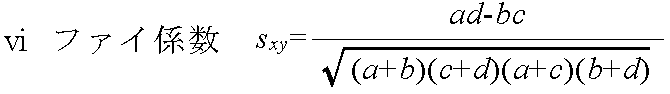
- 順位データ
- 順位データとは,例えば,n 種類のものに対して,各人がそのものに対する好みを 1 から n の値で答えるような場合に得られるデータです.従って,各データは,1,2,・・・,n のいずれかになっていることになります.
- 順位データに対しては,一般に,順位で表現された値を,連続な値に変換し,A で述べた方法を適用するか,または,以下に示すような順位相関係数を使用する方法が使用されます.
- Spearman の順位相関係数
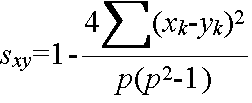
- Kendall の順位相関係数
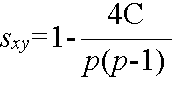
- ただし,C は,以下のような数値とします.まず,データ x を,[1 2 ・・・ n]T となるように各変量を入れ替えます.次に,この順序になるように,データ y を並べ替えます.そして,[1 2 ・・・ n]T となるように並べ替えるのにかかった入れ替え回数を C とします.
- 順位データとは,例えば,n 種類のものに対して,各人がそのものに対する好みを 1 から n の値で答えるような場合に得られるデータです.従って,各データは,1,2,・・・,n のいずれかになっていることになります.
- クラスター数 M = N とする
- クラスター(データ)間の類似度(距離)を計算する
- クラスターの中で最も類似度が大きい(距離が小さい)対を求め,それを 1 つのクラスターに融合する.
- M = M - 1 とし,もし,M > L ならば,融合されたクラスターと他のクラスタとの距離を計算し 3 へ戻り,そうでなければ終了する
- Ci: クラスター i = 1, 2, ・・・, M
- ni: クラスター Ci を構成するデータ数
- Ck: クラスター Ci と Cj の融合によって生成されたクラスター
- Dio: クラスター Ci と残りの他のクラスター Co との距離
- 最短距離法
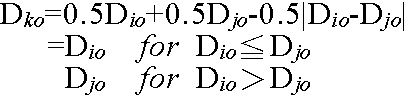
- 最長距離法
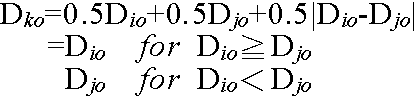
- メジアン法
Dko = 0.5 Dio + 0.5 Djo - 0.25 Dij
- 重心法
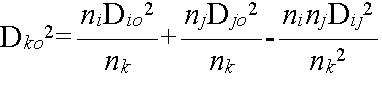
- 群平均法
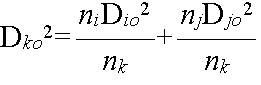
- これは,クラスター間の距離を以下の式によって計算することに相当する.
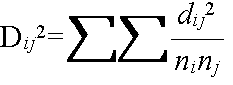
- ただし,ΣΣ dij2 は,クラスター Ci に属するデータと,クラスター Cj に属するデータ間のユークリッド距離の 2 乗を,すべて加え合わせたものとする.
- ウォード法
- クラスターを融合することによって,クラスター Ck の重心まわりの偏差平方和が最小になるように融合する.結局,次の距離が最小になるものを融合する(データ間の距離としては,ユークリッド距離).
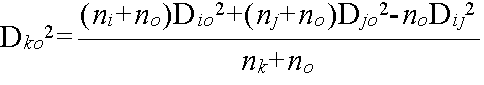
- 例5 : クラスター分析を行うためのC/C++ によるプログラム例 →
 JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「クラスター分析」をご覧ください.
JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「クラスター分析」をご覧ください.
- このプログラムに対して,クラスター間距離を計算する方法(method),クラスタの数(L,クラスタの数がこの値になったら終了),変数の数(n),及び,データの数(N)を与え,続いて,N 組のデータを与えればクラスター分析を実行できます.例として使用したデータは,(N(50, 202), N(50, 202)), (N(30, 152), N(-50, 152)), 及び, (N(-20, 202), N(10, 202)) となるデータを,各々,40,30,及び,30 個発生させたものであり,図示すれば以下のようになります.
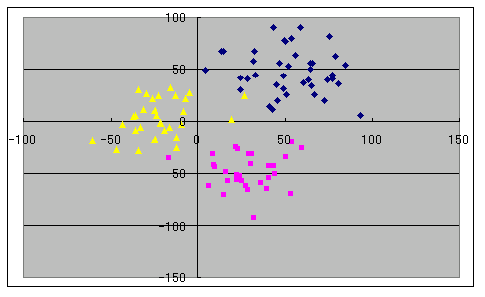
- 以下に,分類するクラスター数を 9,6,及び,3 に設定した場合に対する実行結果を示しておきます.すべてのデータに対して以下のような結果が出るとは限りません.データの種類によって,最適な分類方法を選ぶべきです.
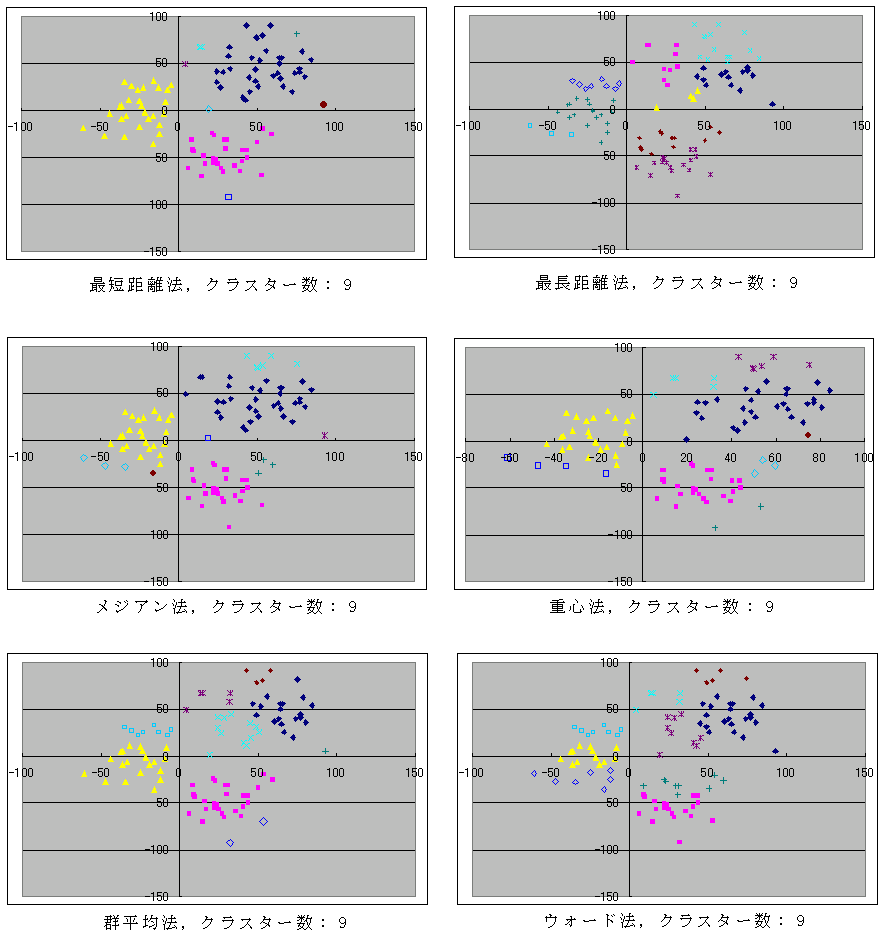
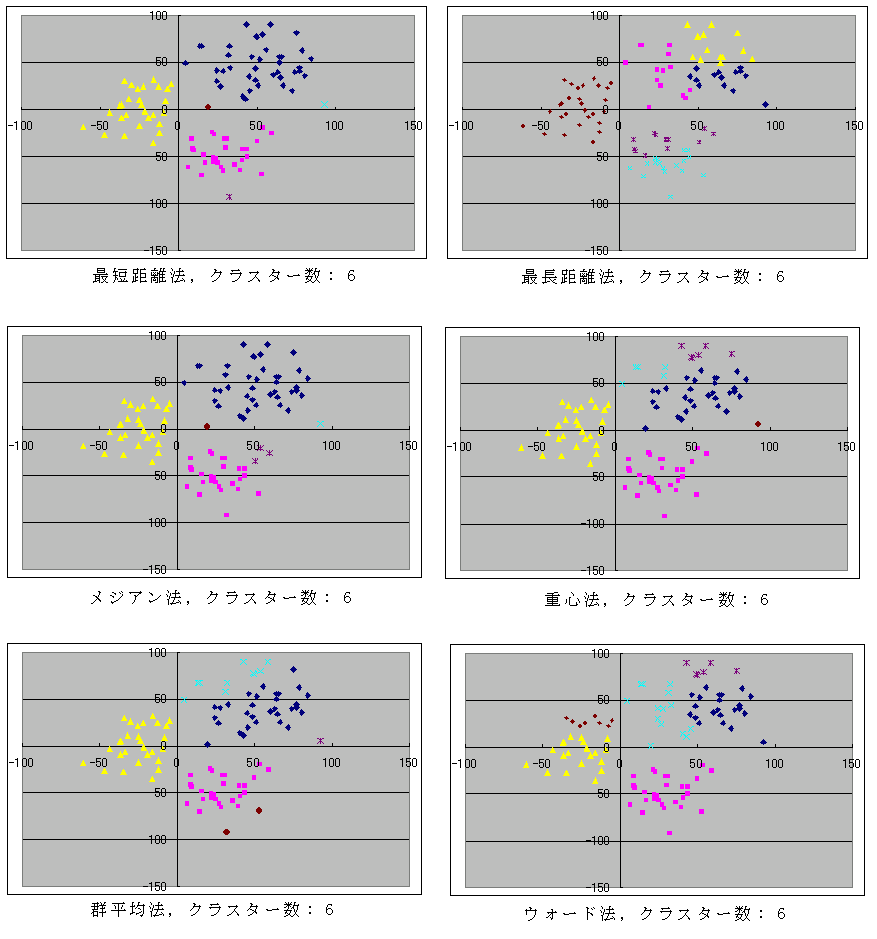
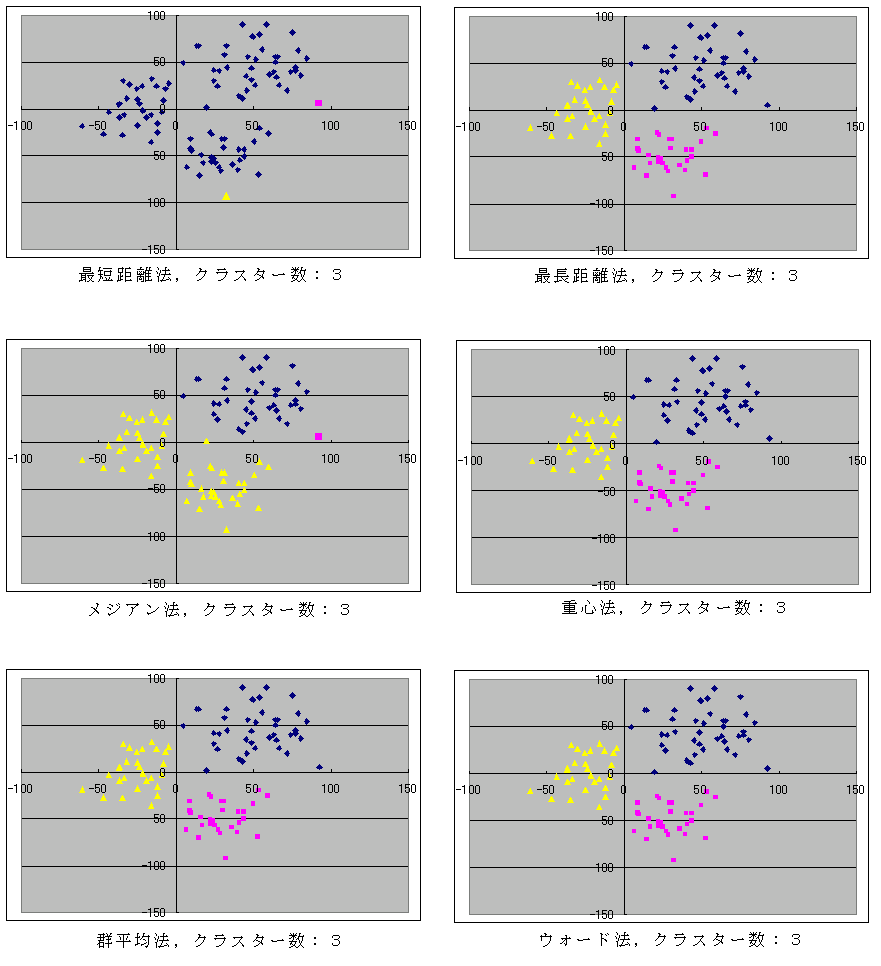
- このプログラムに対して,クラスター間距離を計算する方法(method),クラスタの数(L,クラスタの数がこの値になったら終了),変数の数(n),及び,データの数(N)を与え,続いて,N 組のデータを与えればクラスター分析を実行できます.例として使用したデータは,(N(50, 202), N(50, 202)), (N(30, 152), N(-50, 152)), 及び, (N(-20, 202), N(10, 202)) となるデータを,各々,40,30,及び,30 個発生させたものであり,図示すれば以下のようになります.
xij = μi + εij ( i = 1,2,...,Np, j = 1,2,...,N ) (1)
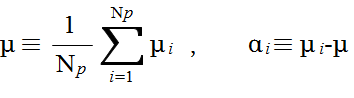
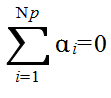
xij = μ + αi + εij ( i = 1,2,...,Np, j = 1,2,...,N ) (2)
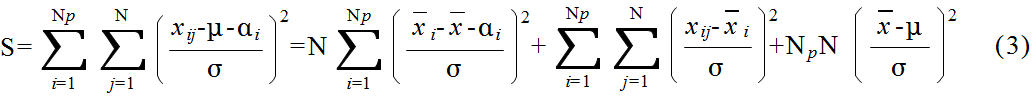
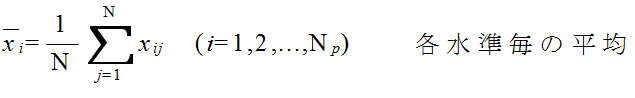
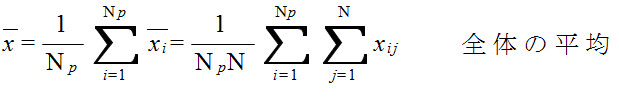
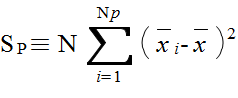
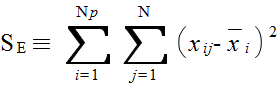
VP ≡ SP / ( Np - 1 ) VE ≡ SE / Np( N - 1 ) F ≡ VP / VE
F0 > F ( Np - 1, Np( N - 1 ) ; α )
| 平方和 | 自由度 | 不偏分散 | F | |
|---|---|---|---|---|
| 全変動 | S | NpN - 1 | ||
| 水準間 | SP | Np - 1 | VP = SP / ( Np - 1 ) | F = VP / VE |
| 水準内 | SE = S - SP | Np( N - 1 ) | VE = SE / Np( N - 1 ) |
- 例6 : 分散分析を行うためのC/C++ によるプログラム例 →
 JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「分散分析」をご覧ください.
JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「分散分析」をご覧ください.
- このプログラムは,一元配置法または二元配置法に対して適用可能です.ただし,各水準における実験回数(データ数)はすべて同じ場合だけを扱っています.なお,分散分析を行う関数は aov であり,他の関数は F 分布における α% 値を計算するためのものです.従って,関数 aov において α% 値を出力しない場合は,aov 以外の関数は必要ありません.
- このプログラムを使用した計算例として,3 つの工場で生産されたある製品の不良率(%)に差があるか否かを有意水準を 5% として検定してみます.各工場で生産された 6 つのロットに対する不良率を調べた結果が以下のようになったとします.
工場1 工場2 工場3 ロット1 3.1 4.7 5.1 ロット2 4.1 5.6 3.7 ロット3 3.3 4.3 4.5 ロット4 3.9 5.9 6.0 ロット5 3.7 6.1 3.9 ロット6 2.4 4.2 5.4 - ここで,帰無仮説 H0 を,
- このプログラムは,一元配置法または二元配置法に対して適用可能です.ただし,各水準における実験回数(データ数)はすべて同じ場合だけを扱っています.なお,分散分析を行う関数は aov であり,他の関数は F 分布における α% 値を計算するためのものです.従って,関数 aov において α% 値を出力しない場合は,aov 以外の関数は必要ありません.
- H0 : 各工場の不良率に差はない
- とし,分散分析を行ってみます.プログラムに対する入力データは,
1 6 5 // 因子の数 各水準におけるデータ数 有意水準(%) 工場 3 // 因子の名前 水準の数 3.1 4.7 5.1 // 各水準に対する1番目のデータ 4.1 5.6 3.7 // 各水準に対する2番目のデータ 3.3 4.3 4.5 // 各水準に対する3番目のデータ 3.9 5.9 6.0 // 各水準に対する4番目のデータ 3.7 6.1 3.9 // 各水準に対する5番目のデータ 2.4 4.2 5.4 // 各水準に対する6番目のデータ
- のようになります(コメント部分は除く).このデータの元でプログラムを実行すると以下のような結果が得られます.
全変動: 平方和 19.22 自由度 17 工場の水準間: 平方和 9.81 自由度 2 不偏分散 4.9039 F 7.81 5%値 3.68 水準内: 平方和 9.41 自由度 15 不偏分散 0.6277
- このように F の値( 7.81 )は F ( 2, 15 ; 0.05 ) = 3.68 より大きくなり,仮説は棄却されます.
xijk = μ + αi + βj + τij + εijk ( i = 1,2,...,Np, j = 1,2,...,Nq, k = 1,2,...,N ) (4)
| 平方和 | 自由度 | 不偏分散 | F | |
|---|---|---|---|---|
| 全変動 | S | NpNqN - 1 | ||
| P の水準間 | SP | Np - 1 | VP = SP / ( Np - 1 ) | FP = VP / VE |
| Q の水準間 | SQ | Nq - 1 | VQ = SQ / ( Nq - 1 ) | FQ = VQ / VE |
| 相互作用 | SI | ( Np - 1 )( Nq - 1 ) | VI = SI / ( Np - 1 )( Nq - 1 ) | FI = VI / VE |
| 水準内 | SE | NpNq( N - 1 ) | VE = SE / NpNq( N - 1 ) |
F0 > FP ( Np - 1, NpNq( N - 1 ) ; α )
F0 > FQ ( Nq - 1, NpNq( N - 1 ) ; α )
F0 > FI ( ( Np - 1 )( Nq - 1 ), NpNq( N - 1 ) ; α )
- 例7 : 分散分析を行うためのC/C++ によるプログラム例 →
 JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「分散分析」をご覧ください.
JavaScript 版では,任意のデータに対して画面上で結果を求めることができます.なお,他の言語( PHP,Ruby,Python,C#,VB )によるプログラム例に関しては,「プログラミング言語の落とし穴」第 9 章の「分散分析」をご覧ください.
- このプログラムは,例6 において使用したものと全く同じです.このプログラムを二元配置法に使用した計算例として,ある作物に対して,栽培時に施す薬剤及び品種によってその収穫量に差があるか否か,また,薬剤と品種の間に相互作用かあるか否かを検定してみます.5 種類の薬剤と 2 つの品種に対して,各 3 つのブロックで栽培し,その収穫量を示したのが以下の表です.なお,収穫量は,基準収穫量からの相対値で表現してあります.
薬剤1 薬剤2 薬剤3 薬剤4 薬剤5 品種1 3 4 12 -4 -4 8 -8 31 12 19 7 -5 8 0 23 品種2 8 -10 9 10 15 -5 11 26 -1 13 10 -6 13 -7 -6 - プログラムに対する入力データは,
- このプログラムは,例6 において使用したものと全く同じです.このプログラムを二元配置法に使用した計算例として,ある作物に対して,栽培時に施す薬剤及び品種によってその収穫量に差があるか否か,また,薬剤と品種の間に相互作用かあるか否かを検定してみます.5 種類の薬剤と 2 つの品種に対して,各 3 つのブロックで栽培し,その収穫量を示したのが以下の表です.なお,収穫量は,基準収穫量からの相対値で表現してあります.
2 3 5 // 因子の数 各水準におけるデータ数 有意水準(%) 薬剤 5 // 1番目の因子の名前 その水準の数 品種 2 // 2番目の因子の名前 その水準の数 3 4 12 -4 -4 // 1番目の因子の各水準に対して,2番目の因子の水準1に対する1番目のデータ 8 -8 31 12 19 // 1番目の因子の各水準に対して,2番目の因子の水準1に対する2番目のデータ 7 -5 8 0 23 // 1番目の因子の各水準に対して,2番目の因子の水準1に対する3番目のデータ 8 -10 9 10 15 // 1番目の因子の各水準に対して,2番目の因子の水準2に対する1番目のデータ -5 11 26 -1 13 // 1番目の因子の各水準に対して,2番目の因子の水準2に対する2番目のデータ 10 -6 13 -7 -6 // 1番目の因子の各水準に対して,2番目の因子の水準2に対する3番目のデータ
- のようになります(コメント部分は除く).このデータの元でプログラムを実行すると以下のような結果が得られます.
全変動: 平方和 3260.80 自由度 29 薬剤の水準間: 平方和 1289.80 自由度 4 不偏分散 322.4500 F 3.37 5%値 2.87 品種の水準間: 平方和 22.53 自由度 1 不偏分散 22.5333 F 0.24 5%値 4.35 相互作用: 平方和 34.47 自由度 4 不偏分散 8.6167 F 0.09 5%値 2.87 水準内: 平方和 1914.00 自由度 20 不偏分散 95.7000
- このように,薬剤の水準間に対する F の値( 3.37 )は F ( 4, 20 ; 0.05 ) = 2.87 より大きくなり,仮説は棄却されます.ただし,品種間の差及び相互作用に関しては棄却されません.
- 数量化分析Ⅰ類: 重回帰分析と同じ目的で使用されます
- 数量化分析Ⅱ類: 判別分析と同じ目的で使用されます
- 数量化分析Ⅲ,Ⅳ類: 主成分分析や因子分析と同じ目的で使用されます