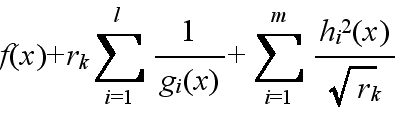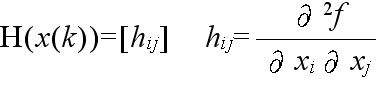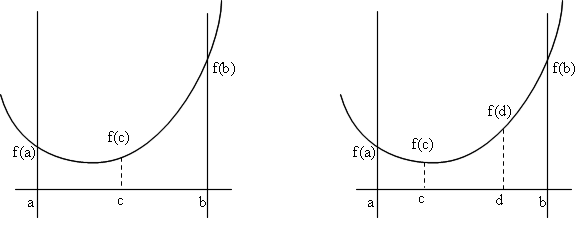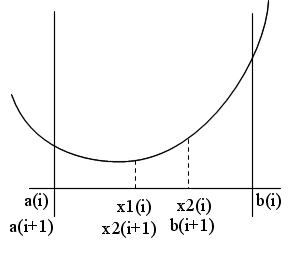非線形計画法

－２．非線形計画法（ NP: Nonlinear Programming ）－

　　非線形計画法（ NP: Nonlinear Programming ）が対象とする問題は以下のように記述できます．問題の記述方法は，基本的に線形計画法が対象とする問題と同じですが，非線形関数を含んでいることだけが異なっています．

目的関数，: y = f(x)　　x = [x₁, x₂, ･･･, x_n]^T　　　(1)
を，制約条件，: h_i(x) ＝ 0,　　i＝1，2，･･･，m　　　(2); g_j(x) ≧ 0,　　j＝1，2，･･･，l　　　(3)
のもとで，最小にする．

　　通常，最適化問題には必ずといって良いほど，制約条件が付加されます．しかし，非線形最適化問題において制約条件が付加されると，問題を解くのが格段に難しくなります．そこで，ここでは，制約条件のない場合に対する解法を中心に話を進めていきます．

　　そこで，制約のある問題について，簡単に触れておきます．等式制約条件だけの場合に対しては，ラグランジュの未定乗数法という有名な方法が存在します．この方法は，ラグランジュ関数，

という関数を導入し，この関数が，x^*, λ^* において局所的最小点となるための必要条件が，

であることを利用して，最小点を求める方法です．

　　次に，一般的な制約がある場合です．制約がある問題をそのまま解く手法も存在しますが，何らかの方法で制約のある問題を制約のない問題に変換して解く手法がよく使用されます．その方法の一つは，ペナルティ関数を使用する方法，ペナルティ関数法です．

　　ペナルティ関数法では，ペナルティ関数 g(x) を導入し，目的関数を，

拡張された目的関数： f(x) + t g(x)

のように変形し，制約のない問題として解を求めようとする方法です．ペナルティ関数法は，ペナルティ関数の性質により以下のように分類できます．

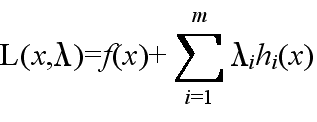
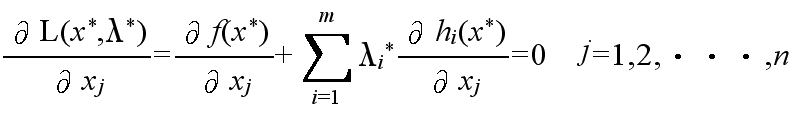
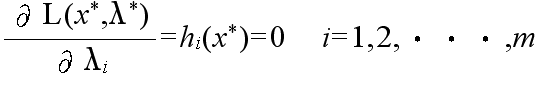
外点法　　g(x) を，x が制約を満たしていれば 0 で，満たしていなければ正の大きな値をとる x の連続関数とします．最初は t を小さな値に設定し（制約をゆるめ），徐々に大きくしながら，目的関数の最小化を行います．

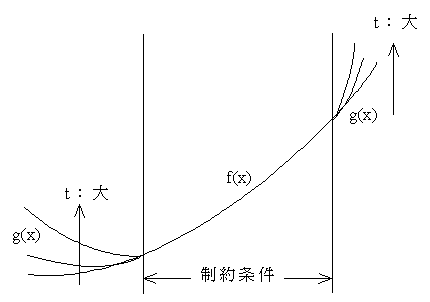
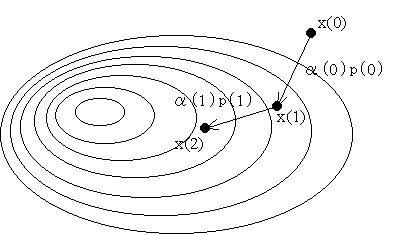
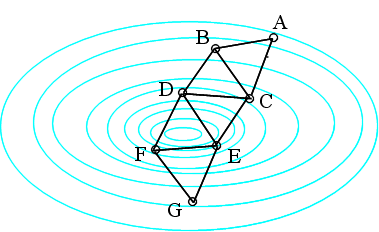
　　概念的な図を書けば上のようになります．t が小さいときは，拡張された目的関数の最小値は，制約条件の外側で，かつ，制約条件の境界から離れた位置にありますが，t が大きくなると制約条件の境界に近づいてきます．
内点法　　g(x) を，x が制約を満たしていれば非負の値をとり，制約の境界条件上の点ならば無限大となる x の連続関数とします．最初は t を大きな値に設定し，徐々に小さくしながら，目的関数の最小化を行います．

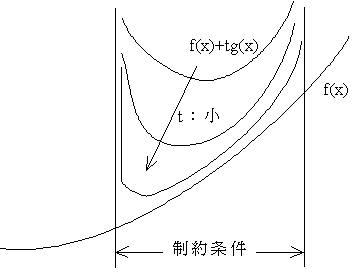
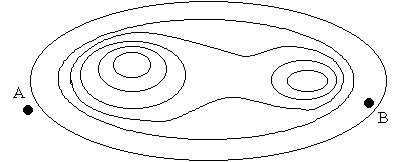
　　概念的な図を書けば上のようになります．t が大きいときは，制約条件内の拡張された目的関数は，本来の目的関数と大きく異なりますが，t が小さくなるにつれ，制約条件の境界に近い部分を除き，本来の目的関数に近づいていきます．

　　ペナルティ関数法として良く知られた方法に，SUMT: Sequential Unconstrained Minimization Technique という方法があります．SUMT では，以下のように目的関数を変換し，最適解を求めようとする方法です（ r_k が，上述の t に相当）．

２．２基本アルゴリズム

　　非線形計画法において使用されるアルゴリズムは，目的関数の勾配情報（微分）を利用するか否かによって，大きく 2 つに分類できます．ここでは，勾配を利用する方法（ 2.4 節～ 2.7 節）に対する基本アルゴリズムについて説明します．その基本アルゴリズムは以下のようになります．なお，勾配を利用しない方法に関しては，「 2.8 シンプレックス法」を参照してください．

適当な x の初期値 x(0) を与え，繰り返し回数を表すパラメータ k を 0 にしておきます．
x(k) が解であるか否かの判定を行います．つまり，最小点であるための必要条件（勾配ベクトル = 0 ），
```
∥∇f(x(k))∥ = ∥[∂f/∂x₁，･･･，∂f/∂x_n]^T∥ = 0			
```
を調べることによって行います．実際上は，厳密に 0 になることはほとんどありませんので，上記の値が，適当な小さな値（ε₁）より小さいか否かによって行います．

　　上記の判定だけですと，場合によっては，プログラムが無限ループに入ってしまう可能性もあります．従って，繰り返し回数がある回数以上になったら終了させることはもちろん，以下に示すような判定基準を併用することもあります．
```
∥f(x(k+1)) - f(x(k))∥ < ε₂
∥x(k+1) - x(k)∥ < ε₃
∥f(x(k))∥ < ε₄			
```
上記の判定の結果，解に収束していない場合は，k 回目の計算結果を基にして，関数値 f を減少させる新しい点 x(k+1) を生成し（下図参照），k = k + 1 として，ステップ 2 へ戻ります．新しい点 x(k+1) は，式，
```
x(k+1) = x(k) + α(k)p(k)			
```
によって計算されます．そのためには，探索方向 p(k) とその方向に沿った歩み幅（ step size ） α(k) を決める必要があります．

　　探索方向 p(k) を決めるための情報として，勾配ベクトル ∇f(x(k)) = [∂f/∂x₁，･･･，∂f/∂x_n]^T や Hesse 行列

等が利用されます．この p(k) の計算方法によって，アルゴリズムが異なってきますが，次節以降で順に説明していきます．一般に，多くの情報を用いれば繰り返しの回数は少なくなりますが，その反面，1 回の点を計算するために必要な計算量が増加します．

　　　歩み幅 α(k) を一定値に固定すると，一般に，f の減少が保証できなくなり，その結果アルゴリズムの収束性が成立しなくなる場合があります．そこで，1 次元探索（次節参照）によって，つまり，
```
f(x(k) + α(k)p(k))			
```
を最小にする α(k) を選択する方法がよく使用されます．

　　以上述べたアルゴリズムにおいて，最も重要な問題は，局所的最適解の問題です．先の図に示したように，山（今まで，最小値を求める方法について説明しましたので，「くぼみ」といった方が良いかもしれませんが，ここでは，最大値を求める問題にすり替え，山という表現を使用します）が一つだけの場合は問題ありませんが，一般には，右図に示すように，多くの山が存在します（多峰性）．最適化アルゴリズムは，これらの山の中から，最も最適なもの（最も高い山）を選び出す必要があります．しかし，上記のアルゴリズムを適用した場合，収束先は，ほとんど初期値によって決まってしまいます．例えば，下図の場合，点 A を初期値とすれば左の山（最適解）へ，また，点 B を初期値とすれば右の山（局所的最適解）へ収束してしまう可能性が非常に高いことになります．

２．３ 1 次元探索手法

　　1 次元探索の目的は，f(x) （x はスカラー）の最小値を求めることです（ f(x) の符号を変えれば最大値を求めることになります)．1 次元探索の手法は，ある方向ベクトル上の最小値を求めるためにも使用できますので，多次元探索の中でも歩み幅 α(k) を決めるためにしばしば使用されます．この節では，代表的な 2 つの手法について説明します．

２．３．１黄金分割法

C/C++によるプログラム例　→　: JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「最適化（黄金分割法）」をご覧ください．

　　区間 [a, b] の中に，f(x) が最小となる点が一つだけあるとします．黄金分割法では，最小点が存在する区間を徐々に狭めていくことによって，最小点を求めようとする方法です．

　　では，どのようにして存在区間を狭めていけばよいでしょうか．少なくとも区間内のいくつかの点における f(x) の値を知らなければ不可能です．下に示す図を見てください．左図のように，区間内の 1 つの点の値を知っただけでは，区間 [a, c]，区間 [c, b] のいずれに最小点があるのかを一般的に知ることはできません．

　　しかし，上の右図のように，区間内の 2 点における f(x) の値を知ることができれば，f(c) と f(d) の大小関係により，区間 [a, d]，区間 [c, b] のいずれに最小点があるかを知ることができます．これに関しては，以下のような定理が存在します．

［定理］ f(x) が区間 [a, b] で単峰性（この区間で，唯一の最小点を持つ）であるとき，最小点の存在範囲を [a, b] の中のより小さい部分区間に狭めるためには，少なくとも区間内の 2 点における関数の値を知る必要がある．

　　次に，「各ステップごとに，最小点を含む区間の幅を一定の比率 τ で減らせるようにできるか？」ということについて考えてみます．実は，これは可能です．以下にその理由（証明）について述べます．

　　今，

[a(i), b(i)] : ある段階における区間
x₁(i), x₂(i) : 区間内の点（x₁(i) < x₂(i)）

としたとき，一定比率 τ で減少するためには，次式を満たす必要があります．

(x₂(i) - a(i)) / (b(i) - a(i)) = (b(i) - x₁(i)) / (b(i) - a(i)) = τ　　(1)

したがって

x₁(i) - a(i) = b(i) - x₂(i)　　(2)

となります．いま，f(x₂(i)) > f(x₁(i)) とすると

b(i+1) = x₂(i)
a(i+1) = a(i)

が成立します．さらに，

x₂(i+1) = x₁(i)

とします．したがって，

(x₂(i+1) - a(i)) / (x₂(i) - a(i)) = (x₁(i) - a(i)) / (x₂(i) - a(i)) = τ　　(3)

となります．また，(2) 式より，

x₁(i) - a(i) = b(i) - a(i) - (x₂(i) - a(i))

という関係が得られますから，両辺を (x₂(i) - a(i)) で割ると，(1)，(3) 式より，

(x₁(i) - a(i)) / (x₂(i) - a(i)) = 1 / τ - 1 = τ

となります．従って，次の関係が得られます．

τ² + τ - 1 = 0　　　∴τ = （5^0.5 - 1) / 2 ≒ 0.618

　　黄金分割法では，この τ を使用します．初期区間 [a(0), b(0)] を与えた後，収束条件（｜b(k) - a(k)｜ < ε）が成立するまで，以下の手続きを繰り返します．

f(x₂(i)) > f(x₁(i)) のとき（上図参照）

a(i+1) = a(i)
b(i+1) = x₂(i)
x₁(i+1) = a(i) + (1 - τ)(b(i+1) - a(i))
x₂(i+1) = x₁(i)

f(x₂(i) ≦ f(x₁(i)) のとき

a(i+1) = x₁(i)
b(i+1) = b(i)
x₁(i+1) = x₂(i)
x₂(i+1) = b(i) - (1 - τ)(b(i) - a(i+1))

２．３．２ 2 次多項式近似による方法

C/C++によるプログラム例　→　: JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「最適化（多項式近似法）」をご覧ください．

　　a₁ < a₂ < a₃，かつ，f(a₁) > f(a₂) < f(a₃) となる 3 点が与えられたとき，この 3 点を通る 2 次多項式，

f(x) = ax² + bx + c

の係数は一意に決まります．また，この関数は，

x = -b / (2a)

で，最小値をとります．2 次多項式近似による方法は，この性質を利用して最小値を求めようとするものです．そのアルゴリズムは以下のようになります．

初期点 x₀ と，初期の刻み幅 δ₀ を与え，k = 0 とします．
x_k+1 = x_k + δ_k とし，f(x_k+1) を計算します．
f(x_k+1) ≦ f(x_k) ならば，δ_k+1 = 2δ_k，k = k + 1 として 2 へ戻ります．
f(x_k+1) ＞ f(x_k) で，かつ，k ≧ 1 ならば，
1. x_k+2 = x_k+1 - δ_k / 2 とし，f(x_k+2) を計算します．
2. δ_k/2 間隔の 4 点 x_k-1，x_k，x_k+2，x_k+1 の内，最小の関数値を与える点から最も遠い点を除去します．
3. 残った 3 点を小さい順に a₁，a₂，a₃ として，5 へ進みます．
f(x_k+1) ＞ f(x_k) で，かつ，k ＝ 0 ならば，
1. f(x₀-δ₀) を計算します．
2. f(x₀-δ₀) ＞ｆ(x₀) ならば，
  1. a₁ = x₀ - δ₀，a₂ = x₀，a₃ = x₁ として，5 へ進みます．
  f(x₀-δ₀) ≦ f(x₀) ならば，
  1. x₁ = x₀ - δ₀，δ₀ = -δ₀，δ₁ = 2δ₀，k ＝ 1 として，2 へ戻ります（反対方向への探索）．
a₁，a₂，a₃ を用いて，2 次多項式近似を作ります（ 3 点を通る 2 次多項式を決定します）．この 2 次多項式の最小点は，δ を 3 点の間隔とすると，

で与えられます．
|Δ|が十分小さければ，
1. ｘを最小点として採用します．
そうでなければ
1. x と a₂ の内，関数値の小さい方を x₀，δ₀ = δ / 2，k ＝ 0 として 2 へ戻ります．

２．４最急降下法（ Steepest Descent Method ）

C/C++によるプログラム例　→　　（ C/C++ 及び Java によるプログラムの使用方法）: JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「最適化（最急降下法）」をご覧ください．

　　2.2節で述べた基本アルゴリズムにおいて，

歩み幅： α(k) = 一定，探索方向： p(k) = -∇f(x(k)) = -[∂f/∂x₁，･･･，∂f/∂x_n]^T

とした方法です．アルゴリズムは簡単であり，ある条件の下で，大域的収束性（任意の初期点から出発しても，特定の性質を持つ点に収束）が保証されますが，収束が遅いという欠点があります．この方法の変形として，歩み幅 α(k) を 1 次元最適化によって求める方法を，最適勾配法( Optimul Gradient Method )と呼びます．

２．５共役勾配法（ Conjugate Gradient Method ）

C/C++によるプログラム例　→　　（ C/C++ 及び Java によるプログラムの使用方法）: JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「最適化（共役勾配法）」をご覧ください．

［定義］ n ｘ n 対称行列 Q に対して，二つの方向を表すベクトル u，v が: u^TQv = 0
を満たすとき，u および v は Q に関して共役であるという．

　　Q を単位行列に選べば，上の式は直交条件に他ならないので，共役性は直交性の拡張概念です．この共役性の概念を利用した方法が共役勾配法であり，アルゴリズムは以下の通りです．

初期点 x(0) を与えます．
k = 0, β(0) = 0 とおきます．
g(k) = ∇f(x(k)) を計算し，∥g(k)∥ < ε ならば，計算を終了します．
p(k) = -g(k) + β(k)p(k-1) とします．ただし，β(k) は以下の式で計算します．
x(k+1) = x(k) + α(k)p(k)とします（α(k) は 1 次元探索で決める）．
k = n - 1 ならば，
1. x(0) を x(n) で置き換え，ステップ 2 へ戻ります
k ≠ n - 1 ならば，
1. k = k + 1 として，ステップ 3 へ戻ります．

　　共役勾配法では，目的関数が以下に示すような 2 次形式ならば，繰り返し計算は n（ベクトル x の次元）回で終了します．

f(x) = 0.5x^TQx + b^Tx

２．６ニュートン法（ Newton 法）

C/C++によるプログラム例　→　　（ C/C++ 及び Java によるプログラムの使用方法）: JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「最適化（ Newton 法）」をご覧ください．

　　目的関数 f(x) を探索点 x(k) の近傍で 2 次多項式に近似すると，以下のようになります．なお，H(x(k)) は，Hesse 行列と呼ばれ，以下に示すように，目的関数 f(x) の 2 階偏微分要素から構成されます．

f(x) ≒ f(x(k)) + ∇f(x(k))^T(x - x(k)) + (x - x(k))^TH(x(k))(x - x(k)) / 2

∇f(x(k)) = [∂f/∂x₁，･･･，∂f/∂x_n]^T

2 次多項式ですので，この式の最小値は x で微分して 0 とおいた式，つまり，

∇f(x(k)) + H(x(k))(x - x(k)) = 0

を解くことによって得られます．従って，H(x(k)) の逆行列が存在すれば，容易に解くことができます．この最小点を x(k+1) とすることによって，次の繰り返し公式を得ることができます．

x(k+1) = x(k) - H(x(k))^-1∇f(x(k))

　　この式から，ニュートン法（ Newton 法）は，基本アルゴリズムにおいて，

歩み幅： α(k) = 1，探索方向： p(k) = - H(x(k))^-1∇f(x(k))

としたものになります．また，この方法の修正版として，α(k) を 1 次元探索で決める方法が考えられます．

　　ニュートン法（ Newton 法）の性質を上げれば，以下のようになります．

解の近傍における収束速度は速いが，初期点を解の近傍に取らなければ収束性が保証されない．
Hesse 行列，および，その逆行列を計算しなければならないことにより，1 回の繰り返し計算あたりの計算量が多い．

２．７準ニュートン法（準 Newton 法）

C/C++によるプログラム例　→　　（ C/C++ 及び Java によるプログラムの使用方法）: JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「最適化（準 Newton 法）」をご覧ください．

　　ニュートン法（ Newton 法）は収束は早いのですが，Hesse 行列の逆行列を計算しなければなりません．そこで，勾配ベクトルを用いて，Hesse 行列の逆行列に収束するような行列の列を，逐次近似によって構成していく方法がいくつか提案されています．これらの方法を，準ニュートン法（準 Newton 法）と呼び，そのアルゴリズムは以下に示す通りです．

初期点 x(0) を与え，k = 0，H(0) = I （単位行列）とします．
g(k) = ∇f(x(k)) を計算し，∥g(k)∥ ＜ ε ならば，計算を終了します．
p(k) = -H(k)g(k)， x(k+1) = x(k) + α(k)p(k) とします（ α(k) は 1 次元探索で決める）．
行列 H(k+1) を計算します．計算方法として，以下のような方法があります．ただし，各方法において，

　　　s(k) ≡ x(k+1) - x(k)， y(k) ≡ g(k+1) - g(k)

とします．
k = k + 1 として，ステップ 2 へ戻ります．

２．８シンプレックス法

C/C++によるプログラム例　→　　（ C/C++ 及び Java によるプログラムの使用方法）: JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「最適化（シンプレックス法）」をご覧ください．

　　最後に，微分を全く使用しない方法について説明します．n 次元空間のシンプレックス（単体）を利用し，最適解を求める方法です．シンプレックスとは，n 次元空間において 0 でない体積を囲む少なくとも ( n + 1 ) 個の点から構成されます．例えば，4 次元空間（ 3 変数関数）においては 4 面体，3 次元空間（ 2 変数関数）においては 3 角形に相当します．シンプレックス法では，初期シンプレックスを与えた後，そのシンプレックスを移動，縮小，又は，拡大しながら最適解に収束させようとします．

　　概念的なことを理解してもらうために，2 変数関数

z = f(x, y)

の最小値を求める場合について，上の図を参照しながら，アルゴリズムの細部は省略して説明します．まず，3 点 A，B，C （初期シンプレックス）を決めます．次に，3 点の内，z の値が最大になる点を選び，その点を他の 2 点から決まる直線に対して対称な位置に移動します．上図においては，点 A が点 D に移動し，新しい三角形 BCD ができます．同じような処理を繰り返すことによって，

B → E，　C → F，　D → G

のように移動していきます．徐々に，Z が最小となる方向に三角形が移動していくことが分かるかと思います．しかし，このまま続けると，点 G が点 D に移動し，同じ状態を繰り返すことになってしまいますので，そのようなときは，三角形の辺の長さを半分にし，同様の処理を繰り返します．三角形の辺の長さが精度的に適切な値になったときアルゴリズムは終了します．具体的なアルゴリズムは以下に示す通りです．

n 変数の場合であれば，(n + 1) 個の初期点を選択します．一般には，1 つの初期点 x₀ を選択した後，その点の座標に，各軸方向の単位ベクトル e_i に初期値決定係数 k を乗じたものを加えた点を残りの初期点とします．
```
x_i = x₀ + k * e_i     i = 1, ･･･, n			
```

(n + 1) 個の点から，以下に示す点を選択します．．

H : 関数値が最大になる点　　f_H = f( x_H )
G : 2 番目に関数値が最大になる点　　f_G = f( x_G )
L : 関数値が最小になる点　　f_L = f( x_L )

点 H を除いた残りの点の重心 x_C を計算し，この重心に関する点 H の鏡映，
```
x_R = 2x_C - x_H			
```
をもとめ，その関数値 f_R = f(x_R) を計算します．
1. もし，この点がより良い点でなければ，つまり，
  f_R ≧ f_H
  であれば，ステップが大きすぎることになるので縮小を行います．
  B>x_N = ( 1 - λ₁)x_H + λ₁x_R, f_N = f( x_N ) ただし，0 < λ₁ < 1, λ₁ ≠ 0.5
2. もし，この点がより良い点であり，かつ，
  f_R < ( f_L + (λ₂ - 1 )f_H) / λ₂ ただし，1 < λ₂
  であれば，この方向にもっと良い点がある可能性があるため，拡張，
  x_E = λ₂x_R - (λ₂ - 1 )x_H, f_E = f( x_E )
  を行い，
  f_E ≦ f_R
  であれば，x_N = x_E とします．
3. 以上述べた以外の場合は，すべて，x_N = x_R とします．
もし，
```
f_N ≧ f_G			
```
である場合は，次の探索において，前と同じことを繰り返すことになるので，シンプレックス全体を縮小します．
```
x_i = 0.5 * (x_i + x_L)   i = 1, ･･･, n+1			
```
次の条件が満たされれば停止し，そうでなければ，2 に戻ります．

システムの最適化

－ ２．非線形計画法（ NP: Nonlinear Programming ） －

－２．非線形計画法（ NP: Nonlinear Programming ）－