集合と写像

1. １．集合
   1. １．１ 集合の定義
   2. １．２ 集合の諸性質
   3. １．３ 場合の数
   4. １．４ 集合の応用
2. ２．関係
3. ３．写像

１．集合

　　集合は，数学，特に代数の基本になっている概念です．集合は，簡単にいえば，ものの集まりです．なぜ，そのようなものが，重要な概念になってくるのでしょうか．

　　我々は，あまり深く考えずに，加減乗除などの演算を行っています．しかし，その背景では，どのような数（の集合）に対して，どのような演算があり，演算結果はどのような数（の集合）になるのかなど，厳密な定義がなされています．実際，集合やその上に定義される演算が異なっていれば，異なる代数系（代数の世界）が生成されます．例えば，ブール代数は，0 と 1 だけの要素からなる集合の上に定義された代数系ですが，通常の演算の世界と同じような形で定義されています．

　　また，後半に述べるように，関数においても集合の概念は重要です．関数は，2 つのものの間の関係を示したものですが，それらのものがどのような集合に属するのかを定義しておく必要があるからです．

１．１ 集合の定義

［定義］　ある定まった範囲にある対象をひとまとめにしたものを集合（ set ）といい，集合を構成する一つ一つの対象を集合の要素あるいは元という．一般に，x が集合 A の要素であるとき，

x ∈ A

と表す．また，逆に，A の要素でないときは

x ∈／ 　A

と表す．

　　特に，集合 A に含まれる要素の数が有限の場合は，そこに含まれる要素の数を n(A) で表す．

　　集合の例として，以下のようなものがあげられます．

例1.1

A = {x | x は整数で，かつ，0 < x < 6}　：　有限集合， n(A) = 5

B = {x | x は正の偶数}　：　無限集合

C = {x | x は実数}　：　無限集合

　　集合 A のように，要素の数が有限の集合を有限集合といいます．また，集合 B や C のように，要素の数が無限の集合を無限集合といいます．有限集合の場合，または，無限集合においても要素の一部だけを記述することによって誤解が生じないような場合は，次のように，要素を羅列して集合を表すこともできます．

D = {1, 2, 3, 4, 5}
E = {2, 4, 6, 8, ･･･}		

　　同じ無限集合であっても，そこに含まれる要素の数は，B と C では異なるような感じがすると思います．しかし，無限集合に対しては，要素の数という言葉を使用できない（常に，無限大になってしまう）ため，濃度という言葉を使用します．濃度に対する詳細な説明は省略しますが，集合 B と C では濃度が異なることになります．特に，集合 B と同じような濃度を持つ（各要素に対して番号付けが可能な）無限集合を可算無限集合といいます．

　　集合にとって重要なのは，あるものが与えられたとき，それが集合の要素か否かを明確に判断できなくてはいけません．例えば，以下に示すものは，集合のように見えても集合ではありません．

F = { x | x は袋井に近い市町村 }

G = { x | x は小さい整数 }

　　集合 X に含まれるすべての要素 x が，集合 Y に含まれるならば，また，そのときに限って，集合 X は，集合 Y に含まれる，または，集合 X は，集合 Y の部分集合（subset）であるといいます．このことを形式的に記述すると，以下のようになります．また，図を使用して表現すると右図のようになります（このような図を，ベン（Venn）図と呼びます）．

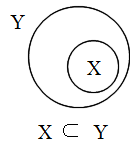
X ⊆ Y　⇔　∀x ∈ X ならば x ∈ Y		

ここで，記号「∀」は，「すべての」と読み，「∀x ∈ X」によって，「集合 X に含まれるすべての要素」を意味します．

　　同様に，2 つの集合が等しいことは，以下のようにして定義できます．

［定義］　X = Y

⇔　∀x ∈ X ならば x ∈ Y，かつ，∀y ∈ Y ならば y ∈ X

⇔　X ⊆ Y，かつ，Y ⊆ X

特に，X ⊆ Y であるが，X ≠ Y のとき，集合 X は，集合 Y の真部分集合であるといいます．

例1.2： X = {1, 2, 3}， Y = {1, 2, 3}， Z = {1, 2, 3, 5} とします．このとき，以下のようなことが言えます．

X = Y （X と Y は等しい）

X ⊆ Y （X は Y の部分集合）

Y ⊆ X （Y は X の部分集合）

X ⊆ Z （X は Z の部分集合）

X ⊂ Z （X は Z の真部分集合）

Y ⊆ Z （Y は Z の部分集合）

Y ⊂ Z （Y は Z の真部分集合）

　　部分集合に対して，対象としているすべての要素を含む集合を全体集合といいます．また，一つも要素を含まない集合を空集合と呼び，φ で表します．

［定義］　2 つの集合X，Y について，そのどちらかに含まれる要素からなる集合を X と Y の和集合といい，

X ∪ Y （= {x | x ∈ X，または，x ∈ Y}）

と表す．X と Y の両方に含まれる要素からなる集合を X と Y の共通集合（積集合）といい，

X ∩ Y （= {x | x ∈ X，かつ，x ∈ Y}）

と表す．また，X の部分集合 E について，X の要素で E に含まれない要素の集合を E の補集合といい，E^c で表す．形式的に，全体集合 X と空集合 φ について

X^c = φ

φ^c = X

とする

　　上の定義で述べた関係をベン図で表現すると，以下のようになります．

　　また，以下の定義も重要です．

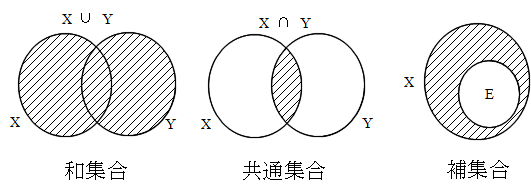
［定義］　集合 S₁ の要素 x と集合 S₂ の要素 y を，この順に順序づけた組 (x, y) 全体がつくる集合を S₁ と S₂ の直積（ちょくせき，direct product，直積集合）といい，S₁×S₂ とかく．

例1.3

1. S₁ = {x | x は実数}，S₂ = {y | y は実数} のとき，S₁×S₂ = {(x, y) | x ∈ X，y ∈ Y} は 2 次元平面における点の集合

2. S₁ = {1, 2}，S₂ = {A, B, C} のとき，S₁×S₂ = {(1, A), (1, B), (1, C), (2, A), (2, B), (2, C)}

　直積に対しては，以下の定理も成立します．

［定理1.1］　有限集合 A，B について

n(A×B) = n(A) × n(B)

が成立する．

１．２ 集合の諸性質

　　以下に述べる集合の諸性質において，

X ： 全体集合

E， F， G ： X の任意の部分集合

とします．

［定理1.2］　有限集合 A，B について

1. 可換律
   E ∪ F = F ∪ E
   E ∩ F = F ∩ E

2. 結合律
   E ∪ ( F ∪ G ) = ( E ∪ F ) ∪ G
   E ∩ ( F ∩ G ) = ( E ∩ F ) ∩ G

3. 分配律
   E ∪ ( F ∩ G ) = ( E ∪ F ) ∩ ( E ∪ G )
   E ∩ ( F ∪ G ) = ( E ∩ F ) ∪ ( E ∩ G )

4. 二重否定律
   ( E^c )^c = E

5. 排中律
   E ∪ E^c = X

6. 矛盾律
   E ∩ E^c = φ

7. ド・モルガン律
   ( E ∪ F )^c = E^c ∩ F^c
   ( S ∩ F )^c = E^c ∪ F^c

　　上の定理の証明は，ベン図を描いてみれば明らかだと思います．同様に，有限集合に対しては，要素の個数について以下の定理が成り立ちます．

［定理1.3］

1. n( E ∪ F ) = n(E) + n(F) - n( E ∩ F )

2. E ∩ F = φ のとき，n( E ∪ F ) = n(E) + n(F)

3. n(E^c) = n(X) - n(E)

１．３ 場合の数

　　ある事柄 A について，A の起こりうるすべての場合の総数を「 A の起こる場合の数といいます．例えば，

A： サイコロを振ったとき偶数がでる事柄

とすれば，A の起こる場合の数は 3 になります．具体的に A は，サイコロを振って 2，4，または，6 がでる場合に相当し，集合で表現すれば，

{2, 4, 6}		

になります．この集合を同じ文字 A で表せば，A の起こる場合の数は，集合 A の要素の数 n(A) になります．つまり，場合の数とは，集合における要素の数に相当します．

　　2 つの事柄 A，及び，B が同時に起こらない場合，2 つの事柄は排反（exclusive）するといい，同じ文字を使用した集合で表現すれば，

A ∩ B = φ		

を意味します．例えば，

A： サイコロを振ったとき偶数がでる事柄

B： サイコロを振ったとき奇数がでる事柄

C： サイコロを振ったとき 3 以上がでる事柄

において，事柄 A と B は排反しますが（同時に起こりませんが），事柄 A と C は排反しません（同時に起こる場合があります）．排反する事柄に対しては以下の定理が成立します．これは，定理1.3 の 2 番目を言い換えたものに過ぎません．

［定理1.4］（和の法則）　2 つの事柄 A，B が同時に起こらないとき，A または B が起こる場合の数は

n(A) + n(B)

である．

　　事柄 A に続いて 事柄 B が起こる事柄を，集合で表すと直積 A × B となります．従って，定理1.1 と同様，以下の定理が成立します．

［定理1.5］（積の法則）　事柄 A の場合の数を n(A)，事柄 B の場合の数をn(B) とすると，事柄 A に続いて事柄 B が起こる場合の数は，

n(A) × n(B)

である．

１．４ 集合の応用

　　ここでは，集合の考え方を理解するために，集合を利用したいくつかの問題を解いてみます．

例1.4　1 から 200 までの整数の集合 A があったときに，以下の問に答えなさい．

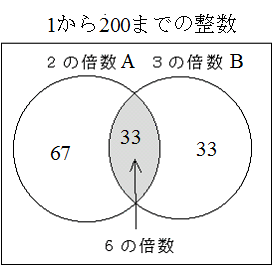
1. A の中に 2 の倍数でも 3 の倍数でもある数は何個ありますか．
   2 と 3 の最小公倍数である 6 の倍数の数を数えれば良い．6 の倍数の数は 200 / 6 = 33 個となる．　A ∩ B

2. A の中に 2 の倍数または 3 の倍数となる数は何個ありますか．
   2 の倍数が 100 個，3 の倍数が 66 個あるので，上図と a より，100 + 66 - 33 = 133 個となる．　A ∪ B

3. A の中に 2 の倍数だが 3 の倍数ではない数は何個ありますか．
   2 の倍数が 100 個あるので，上図と a より，100 - 33 = 67 個となる．

例1.5　100 人を対象に，やったことがあるスポーツについて調査をしました．その結果，ゴルフをしたことがある人は 46 人，テニスをしたことがある人は 37 人，ゴルフもテニスもしたことがない人は 23 人いました．この結果に基づき，以下の問に答えなさい．

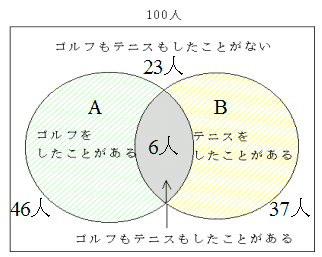
1. ゴルフもテニスもしたことがある人は，何人いますか．
   上図より，n(A) + n(B) + 23 - 100 = 6 人

2. ゴルフをしたことはあるが，テニスはしたことがない人は何人いますか．
   上図より，n(A) - 6 = 40 人

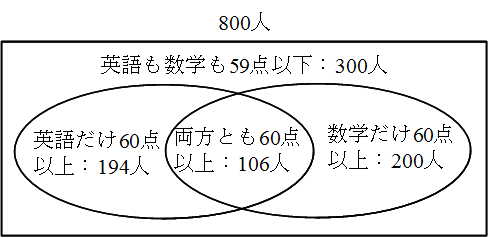
例1.6　800 人が英語，数学，国語の 3 科目に対して 100 点満点のテストを行った結果，以下に示すような結果になりました．英語も数学も 60 点以上という人が 106 人いました．英語が 60 点未満の人のうちの半分は国語が 60 点以上だといいます．また，数学も国語も 60 点以上の人が 118 人，そのうち 3 科目とも 60 点以上である人は 34 人いるといいます．

科目	60 点以上	60 点未満
英語	300 人	500 人
数学	306 人	494 人
国語	352 人	448 人

1. 英語も数学も 60 点未満の人は何人いることになりますか．　下図より，300 人

   

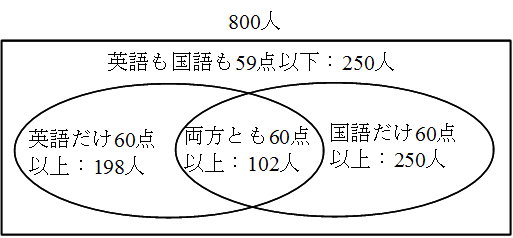
2. 英語と国語の両方が 60 点以上の人は何人いることになりますか．　下図より，102 人

   

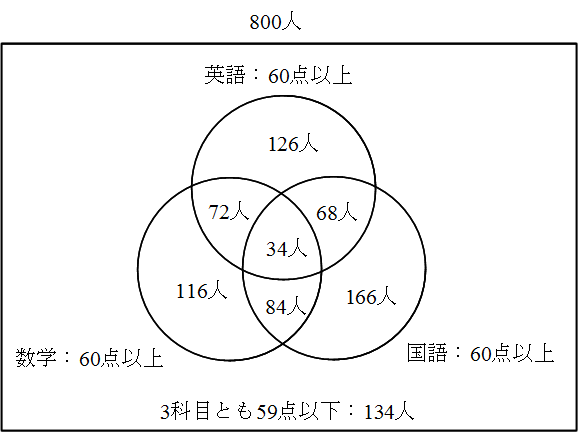
3. 3 科目のいずれも 60 点未満の人は何人いることになりますか．　下図より，134 人

   

例1.7　50 円玉，100 円玉，及び，500 円玉の 3 種類の硬貨を使用して 1000 円を支払いたいとします．このとき，お金の支払い方法は何通りありますか．ただし，使わない硬貨があってもよいものとします．

すべての場合を数は，以下に示すように 18 通りとなる．

500円硬貨枚数	2	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0
100円硬貨枚数	0	5	4	3	2	1	0	10	9	8	7	6	5	4	3	2	1	0
50円硬貨枚数	0	0	2	4	6	8	10	0	2	4	6	8	10	12	14	16	18	20

２．関係

　　2 つの成分 a，b を ( a, b ) のように並べたものを順序対と呼びます．また，順序対の第 1 成分 x が集合 S₁ の要素，第 2 成分 y が集合 S₂ の要素であるとき，順序対 ( x, y ) のすべての集合を，2 つの集合 S₁，S₂ の直積（直積集合）と呼び，S₁ × S₂ のように記述します．

　　今，2 つの集合 S₁，S₂ が各々自然数の集合であったとします．直積集合の要素のうち，第 2 成分が 第 1 成分の倍数になっている要素，たとえば，( 2, 4 )，( 3, 6 ) のような要素のすべての集合 M を考えます．明らかに，集合 M は，直積集合 S₁ × S₂ の部分集合となっています．このような部分集合 M を，S₁ から S₂ への関係（ relation ）と呼びます．この例の場合は，関係 M は「 y が x の倍数である関係」となり， ( x, y ) ∈ M であることを，

x M y		

と記述します．

　　関係は，上の例のように，数値的なものだけに定義されるわけではありません．今，A 及び B を，各々，A 町及び B 町の住人の集合とします．このとき，A 町の住人と B 町の住人との友人関係 M を定義できます．たとえば，太郎は A 町の住人，次郎，三郎，及び，花子が B 町の住人であり，次郎及び三郎は太郎の友人であり，花子は友人でなかったとします．このような場合，友人関係 M によって，

太郎 M 次郎，太郎 M 三郎

のように記述できます．つまり，(太郎，次郎) ∈ M，(太郎，三郎) ∈ M となりますが，(太郎，花子) は M には含まれません．

３．写像

　　写像は，関係の特別なものです．集合 S₁ から 集合 S₂ への関係 M が次の条件を満たすとき関係 M を写像（ mapping, map ）と呼びます．

1) S₁ の任意の元 x は必ず S₂ のある元 y に関係する．

2) 1つの x が異なる 2 つ以上の y に関係しない．

厳密に写像を定義すると，以下のようになります．

［定義］　S₁， S₂ を集合とするとき，S₁ の任意の要素を S₂ の 1 つの要素に対応させる規則 φ を，S₁ から S₂ への写像とよび，

φ ： S₁ → S₂

と書く．このとき，S₁ を φ の定義域，S₂ を値域という．また，S₁ の要素 x が S₂ の要素 y に対応することを

φ ： x |→ y

と書く．y は φ(x) とも書かれ，φ(x) を x の像，x を y の原像という．

　　上の定義によると，先に述べた友人関係 M は写像ではありません．しかし，

a) 集合 A を B 町に友人を持っている人だけに限定する

b) B 町に持っている友人に対して，何らかの条件を付加し，1 名だけに限定する

のような修正を加えれば，友人関係 M は写像となります．

　　また，普段我々が使用している関数はまさに写像そのものです．例えば，

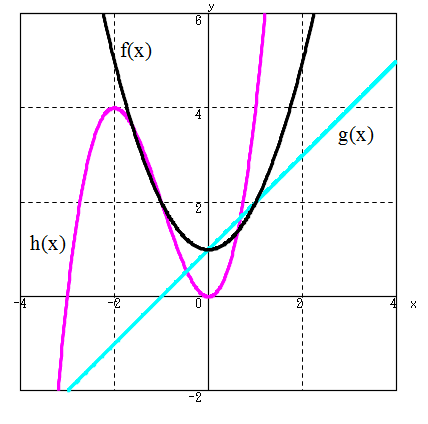
y = f(x) = x2 + 1		

という関数について考えてみます．この関数において，変数 x に任意の実数を代入すれば，関数値 y （実数値）が得られます．つまり，関数（規則） f は，定義域と値域が共に実数の集合 R である写像となっています．従って，この関数を写像の定義に従った書き方をすれば以下のようになります．

f ： R → R
f ： x |→ y = x2 + 1		

関数によっては，多値関数（ ある x に対して複数の y の値を持つ関数）のように，そのままでは写像の条件を満たさない場合もありますが，上で述べた友人関係のように，定義域や値域を適当に再設定してやれば写像の条件を満たすように定義可能です．

　　関数は，関係の特別な場合ですから，関係としての表現も可能です．上の例の場合，「 y = x² + 1 」となる関係を M とすれば，この関数は，

( 2, 5 )，( 1, 2 )，(1.5, 3.25 )，・・・ ∈ M		

のように，直積集合 R × R の部分集合 M に含まれる要素の集合と同等なものとなります．

　　次に，関数 f(x) と同様，定義域と値域を R とした関数，

y = g(x) = x + 1
y = h(x) = x3 + 3x2		

という関数について考えてみます．これらの関数は，先に述べた関数 f(x) と共に図示すれば，下のようになります．

　　いずれの関数においても，x の値が決まれば y の値が決まる点では同じです．しかし，関数 g(x) においては，任意の y を与えたとき，x の値は一意に決まりますが，関数 h(x) や f(x) においては，必ずしも一意とは限りません．例えば，右図からも明らかなように，y の値が 2 となる x の値は複数個存在します．さらに，関数 f(x) においては，1 未満の y に対応する x の値は存在しません．このように，関数（写像）毎に，定義域と値域との関係が異なってきます．この点に関する定義が，以下に示すものです．この定義に従えば，関数 g(x) は全単射，関数 h(x) は全射ではあるが単射ではない，また，関数 f(x) は全射でも単射でもないことになります．

［定義］　写像 φ ： S₁ → S₂ について，任意の x₁，x₂ ∈ S₁ に対し，x₁ ≠ x₂ ならば，φ(x₁) ≠ φ(x₂) であるとき，φ は 1 対 1 の写像，または，単射であるという．また，写像 φ ： S₁ → S₂ が，すべての y ∈ S₂ に対し，φ(x) ＝ y となる x ∈ S₁ をもつとき，φ は S₁ から S₂ の上への写像，または，全射という．写像 φ が全射で単射であるとき φ は全単射という．