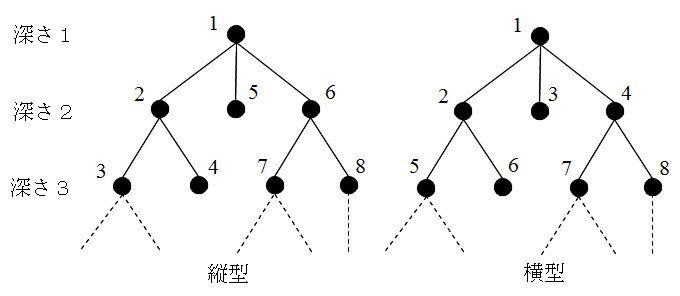
- 分枝操作: 与えられた問題 P0 を,それらを解くことで等価的に P0 が解かれるような,つまり,
f(P0) = min f(Pi) f(P0),f(Pi): 問題 P0 及び Pi の最適値
- となるような部分問題 Pi(i = 1,2,・・・)に分解する操作です.ただし,最適化問題 Pi は,以下に示すような問題とします.
目的関数: f(x) 制約条件: x ∈ Si, Si ⊂ Xi, Xi ⊂ X, S = S ∩ (∪ Xi), Si = S ∩ Xi
- 限定操作: 部分問題 Pi を何らかの方法で終端させます.つまり,それ以上部分問題に分割させないようにします.そのために,部分問題 Pi よりも制約条件が緩く,解きやすい問題を考えて P’i と置きます.このような問題を緩和問題と呼び,問題 Pi の緩和問題 P’i は,以下のように定義されます.
目的関数: g(x) 制約条件: x ∈ S’i, Si ⊂ S’i ⊂ Xi
- 制約条件を緩めてありますので,一般に,x ∈ Si となる x に対しては,g(x) ≦ f(x) のような結果になるはずです.緩和問題の性質を一般的に述べれば以下のようになり,これらの性質を利用して終端させることになります.
- g(P’i) ≦ f(Pi) g(P’i): P’iの最適値(下界値と呼びます)
- P’i が許容解を持たなければ,Pi も持たない.
- P’i の目的関数に g(x) = f(x) を用いるとき,P’i の最適解が Pi の許容解であれば,それは Pi の最適解でもある.
- それまでに他の部分問題によってもとの問題 P0 の許容解が求められており(その中の最小値を z とする),g(P’i) ≧ z なる関係があるとき,部分問題 Pi,及び,それから生成される部分問題に対する許容解は z 以上の値を持つ.
- 初期設定: A = {P0}, z = ∞
- A = φ ならば終了.
- z = ∞: 問題 P0 は解を持たない
- z < ∞: f(P0) = z
- 集合 A の中から,部分問題 Pi を選択(選択方法に関しては後述)
- もし,緩和問題 P’i が解を持たなければ,
- A = A - {Pi} として,2 へ戻る
- そうでなけでば,
- もし,g(P’i) = f(Pi) として,Pi の最適値が得られたら,
- z = min {z, f(Pi)}, A = A - {Pi} として,2 へ戻る.
- そうでなければ
- もし,g(P’i) ≧ z ならば
- A = A - {Pi} として,2 へ戻る.
- そうでなければ
- 問題 Pi を,部分問題 Pi1,・・・,Pik に分解し, A = (A - {Pi}) ∪ {Pi1,・・・,Pik} として,2 へ戻る.
- 発見的探索: 各部分問題 Pi に対し,f(Pi) の推定値 h(Pi) を何らかの方法で求めておき,h(Pi) が最小の部分問題を選ぶ方法です.良い h が見つかれば,非常に優れた方法です.
- 最良下界探索: 発見的探索における h(Pi) として,下界値 g(P’i) を利用する方法です.
- 深さ優先探索: 深さが最大のものから,h あるいは g を基準に選択します.ある部分問題が分解されると,その分解された部分問題から選ばれることになります.この操作が,部分問題が終端されるまで繰り返され,終端されるとバックトラック(たどってきた道筋を戻る)します.
- 幅優先探索: 深さが最小のものから,h あるいは g を基準に選択します.
- 0-1 ナップザック問題
- 目的関数: f(x) = -Σcjxj j = 1, ・・・, n (符号を変え,最小値問題に変換してある)
- 制約条件: Σajxj ≦ b xj = 0 or 1
- たとえば,最大利益を上げる投資先を決定する問題の場合,各変数は以下のようなものに相当します(カッコ内は,本来のナップザック問題).
- n: 投資先の数(品物の数)
- aj: j 番目の計画の必要経費( j 番目の品物の重さ)
- cj: j 番目の計画の期待利益( j 番目の品物の効用)
- b: 投資金額の上限(ナップサックの容量)
- xj: =0: 投資先 j に投資しない(品物 j を入れない)
=1: 投資先 j に投資する(品物 j を入れる)
- 目的関数: f(x) = -Σcjxj j = 1, ・・・, n (符号を変え,最小値問題に変換してある)
- 0-1 ナップザック問題に対する緩和問題 xj の値として連続値を許す
- 目的関数: f(x) = -Σcjxj j = 1, ・・・, n
- 制約条件: Σajxj ≦ b 0 ≦ xj ≦ 1
- 0-1 ナップザック問題に対する緩和問題の解法
- xj を,cj / aj が小さい(最大値を求める場合は,大きい)順に優先度が高いとみなします.
- 優先度順に xj = 1 とおいていきます.ただし,xj = 1 とおくと条件式が満たされなくなる場合には,その xj を xj = k(1 / aj) (k は定数)とおき,制約条件の等式が成立するように k を決定します.それ以降の xj については xj = 0 とおきます.
- 目的関数: f(x) = -Σcjxj j = 1, ・・・, n
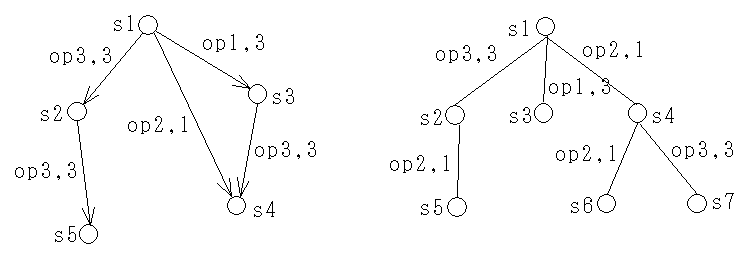
- [節点 0 ] 問題 P0
- 目的関数: f = -2x1 - 5x2 - 4x3 - 3x4
- 制約条件: x1 + 3x2 + 3x3 + 3x4 ≦ 6
- の緩和問題を,変数の優先度,
- x1 → x2 → x3 → x4
- を利用して解くと,以下のようになります.
- (x1, x2, x3, x4) = (1, 1, 2/3, 0) のとき g(x) = -29/3
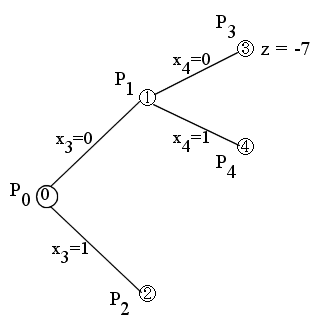
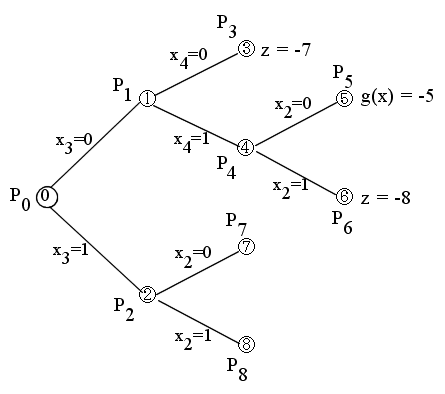
- 明らかにこの解は,元の問題 P0 の解ではありません(制約条件を満たしていない)ので,z = ∞ とおき,変数 x3 の値により,2 つの部分問題 P1 と P2 (接点 1 と接点 2 )に分解します.
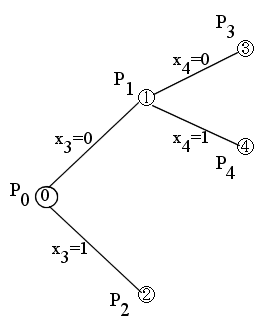
- 目的関数: f = -2x1 - 5x2 - 4x3 - 3x4
- [節点 1 ] 問題 P1 (x3 = 0)
- 目的関数: f = -2x1 - 5x2 - 3x4
- 制約条件: x1 + 3x2 + 3x4 ≦ 6
- を解くと,以下のようになります.
- (x1, x2, x3, x4) = (1, 1, 0, 2/3) のとき g(x) = -9
- この解も,元の問題 P0 の解ではありませんので,変数 x4 の値により,2 つの部分問題 P3 と P4 (接点 3 と接点 4 )に分解します.
- 目的関数: f = -2x1 - 5x2 - 3x4
- [節点 3 ] 問題 P3 (x3 = 0, x4 = 0)
- 目的関数: f = -2x1 - 5x2
- 制約条件: x1 + 3x2 ≦ 6
- を解くと,以下のようになります.
- (x1, x2, x3, x4) = (1, 1, 0, 0) のとき g(x) = -7
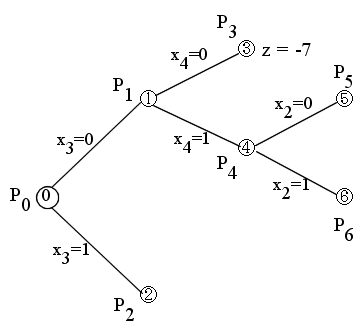
- この解は,元の問題 P0 の解となりますので,z = -7 とおき,終端とします.
- 目的関数: f = -2x1 - 5x2
- [節点 4 ] 問題 P4 (x3 = 0, x4 = 1)
- 目的関数: f = -2x1 - 5x2 - 3
- 制約条件: x1 + 3x2 + 3 ≦ 6
- を解くと,以下のようになります.
- (x1, x2, x3, x4) = (1, 2/3, 0, 1) のとき g(x) = -25/3
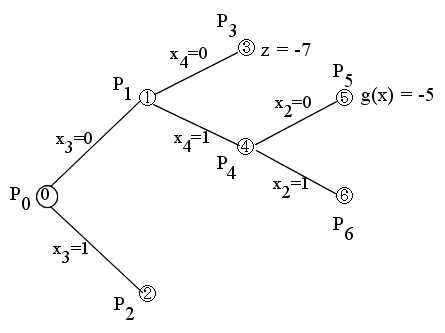
- この解は,元の問題 P0 の解ではなく,かつ,g(x) < z ですので,変数 x2 の値により,2 つの部分問題 P5 と P6 (接点 5 と接点 6 )に分解します.
- 目的関数: f = -2x1 - 5x2 - 3
- [節点 5 ] 問題 P5 (x2 = 0, x3 = 0, x4 = 1)
- 目的関数: f = -2x1 - 3
- 制約条件: x1 + 3 ≦ 6
- を解くと,以下のようになります.
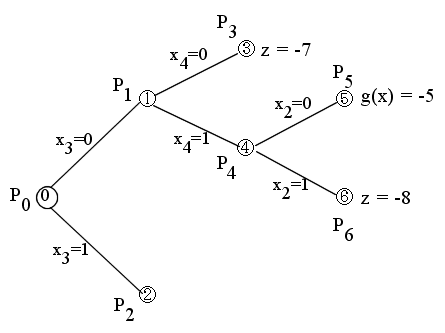
- (x1, x2, x3, x4) = (1, 0, 0, 1) のとき g(x) = -5
- この解は,元の問題 P0 の解ですが,g(x) ≧ z ですので,終端とします.
- 目的関数: f = -2x1 - 3
- [節点 6 ] 問題 P6 (x2 = 1, x3 = 0, x4 = 1)
- 目的関数: f = -2x1 - 5 - 3
- 制約条件: x1 + 3 + 3 ≦ 6
- を解くと,以下のようになります.
- (x1, x2, x3, x4) = (0, 1, 0, 1) のとき g(x) = -8
- この解は,元の問題 P0 の解となります.さらに,g(x) < z ですので,z = -8 とおき,終端とします.
- 目的関数: f = -2x1 - 5 - 3
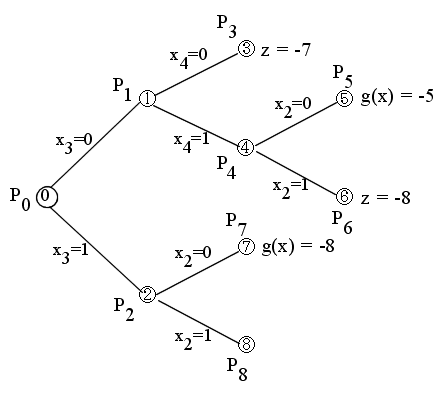
- [節点 2 ] 問題 P2 (x3 = 1)
- 目的関数: f = -2x1 - 5x2 - 4 - 3x4
- 制約条件: x1 + 3x2 + 3 + 3x4 ≦ 6
- を解くと,以下のようになります.
- (x1, x2, x3, x4) = (1, 2/3, 1, 0) のとき g(x) = -28/3
- この解は,元の問題 P0 の解ではなく,かつ,g(x) < z ですので,変数 x2 の値により,2 つの部分問題 P7 と P8 (接点 7 と接点 8 )に分解します.
- 目的関数: f = -2x1 - 5x2 - 4 - 3x4
- [節点 7 ] 問題 P7 (x2 = 0, x3 = 1)
- 目的関数: f = -2x1 - 4 - 3x4
- 制約条件: x1 + 3 + 3x4 ≦ 6
- を解くと,以下のようになります.
- (x1, x2, x3, x4) = (1, 0, 1, 2/3) のとき g(x) = -8
- この解は,元の問題 P0 の解ではなく,かつ,g(x) ≧ z ですので,終端とします.
- 目的関数: f = -2x1 - 4 - 3x4
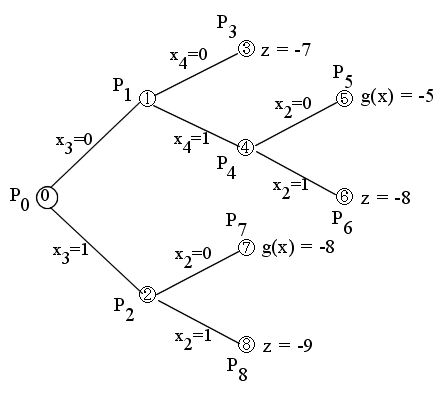
- [節点 8 ] 問題 P8 (x2 = 1, x3 = 1)
- 目的関数: f = -2x1 - 5 - 4 - 3x4
- 制約条件: x1 + 3 + 3 + 3x4 ≦ 6
- を解くと,以下のようになります.
- (x1, x2, x3, x4) = (0, 1, 1, 0) のとき g(x) = -9
- この解は,元の問題 P0 の解であり,かつ,g(x) < z ですので,z = -9 とおき,終端とします.
- 目的関数: f = -2x1 - 5 - 4 - 3x4
P0 → P2 → P8 → P7 → P1