システムのモデルとシミュレーション

1. １．システムのモデル
2. ２．微分方程式モデル
   1. ２．１ 物理システムの微分方程式による記述
   2. ２．２ 微分方程式の解析解
      1. ２．２．１ 解析解の求め方
      2. ２．２．２ 特性方程式の解とシステムの挙動
   3. ２．３ シミュレーション（微分方程式の数値解）
   4. ２．４ 具体例
3. ３．待ち行列モデル
   1. ３．１ 待ち行列
      1. ３．１．１ 確率過程
      2. ３．１．２ 待ち行列システム
      3. ３．１．３ 待ち行列システムの解析
   2. ３．２ 乱数とモンテカルロ法
      1. ３．２．１ 乱数の生成
      2. ３．２．２ 種々の分布に従う乱数
   3. ３．３ 待ち行列問題のシミュレーション

１．システムのモデル

　　実際のシステムを作成し，それを用いてそのシステムの評価を行いながら，解析・設計を進めていく方法は，最も確実な方法でしょうが，経済的等の理由から不可能な場合がほとんどであると思われます．対象とするシステムのモデルを作成し，そのモデルに従って，システムの解析，設計等を行う方法が一般的です．

　　システムのモデルを作成する方法としては，例えば，上図に示すようなものがあります．ただし，対象とするシステム，また，その目的等によって，モデル化の手法は異なってきます．例えば，エレベータについて考えてみます．エレベータの速度，加速度，停止位置等の制御方法を設計することを目的とするならば，微分方程式モデル（決定論的モデル・線形or非線形モデル・動的モデル）を選択することが多いはずです．

　　しかし，あるビルの中に，どのようなタイプ（速度，停止階，大きさ）のエレベータを，何台設置すべきかを検討するような場合，微分方程式モデルでは役に立ちません．例えば，待ち行列モデル（確率論的モデル・動的モデル）などが使用されるはずです．また，エレベータ内部や外部のボタン（目的の階，扉の開閉）が押された場合に対するロジックの設計を行いたい場合は，別のモデルが選択されるはずです．

　　ここでは，数学モデルの内，決定論的及び確率論的なモデルの代表である，微分方程式モデル及び待ち行列モデルに関して，その解析モデルと計算機モデル（シミュレーションモデル）について簡単に解説します．

２．微分方程式モデル

　　決定論的モデル・線形or非線形モデル・動的モデルの代表例である微分方程式モデルについて説明します．微分方程式モデルは，先のエレベータの例で述べましたように，システムの制御方式等を検討する際には欠かせないモデルです．

　　ここでは，右図に示すような，剛体の倒立振り子を例にして，モデルの作成方法，作成されたモデルの解析方法等について説明します．

２．１ 物理システムの微分方程式による記述

　　右図に示す倒立振り子の運動を微分方程式によって記述してみます．棒は剛体とし，棒の質量は m，長さは 2r，重心は中心にあるとします．また，重力の加速度を g とします．このとき，このシステムに働く力は，図に示したように，

mg : 重力の加速度によって，重心に働く下向きの力

F : 床からの水平抗力

G : 床からの垂直抗力

となります．従って，重心の運動は，以下に示す微分方程式によって記述することができます．

　　また，重心回りの運動は，棒の慣性モーメントを I （= (2r)² / 12） とすると，

と書き表せます．ただし，

k : 角速度に比例する摩擦の比例係数

u : 外力

とします．

　　図より，

x = r sinθ

y = r cosθ

という関係が得られますので，これらの関係を利用することによって，最終的に以下に示す微分方程式を得ることができます．この 2 階の定係数非線形常微分方程式が，倒立振り子システムの微分方程式モデルになります．このモデルは，棒が剛体である場合であり，棒のたわみ等を考慮したい場合は，別の微分方程式モデル（偏微分方程式モデル）になります．

　　また， DD>

とおくと，(1) 式は，

のように，1 階の連立微分方程式に変換できます．一般に，n 階の微分方程式は，適当な変数変換によって，1 階の n 元連立微分方程式に変換可能です（変換方法は，一意ではありません）．この連立微分方程式のことをシステムの状態方程式，また，x₁, x₂, ･･･ 等をシステムの状態と呼びます．

２．２ 微分方程式の解析解

２．２．１ 解析解の求め方

　　次は，得られたモデルを使用して，システムの解析，設計を行う段階に入ります．システムを解析する手段としては様々な方法が考えられますが，その一つは，得られた微分方程式を解析的に解くことです．(1) 式は，非線形の微分方程式です．残念ながら，一般の非線形微分方程式を解析的に解く方法は存在しません．

　　ほとんどの実在システムにおいて，システムの状態は，時間と共に，連続的に，かつ，なめらかに変化していくのが普通です．従って，ある状態の近傍だけを考えれば，線形システムと考えても大きな誤差が生じないのが普通です．そこで，(1) 式を，θ = ｄθ/dt = 0 の近傍で線形化すると（この例では，sinθ を，マクローリン展開し，θ の 2 次以上の項を無視する），以下のようになります．

また，状態方程式は，

とおくと，

のように書き表せます．

　　定係数 n 階線形微分方程式

は，一般に，解析的に解くことが可能です．ここでは，2 階の微分方程式，

を例に取り，解析解の求め方について説明していきます．今，入力項 r(t) = 0 と置いた，

を，補助方程式と呼びます．このとき，微分方程式の解には，以下のような性質があります．

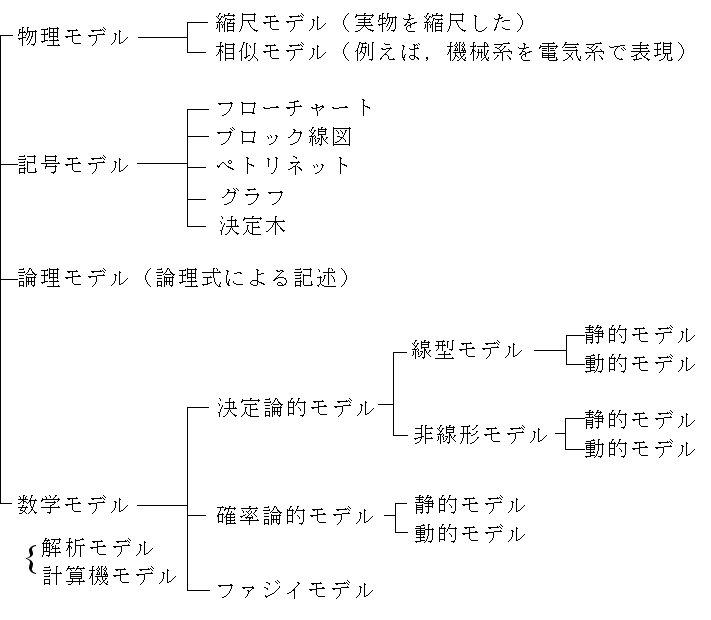
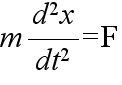
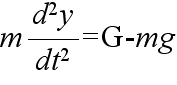
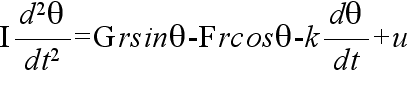
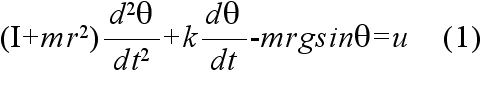
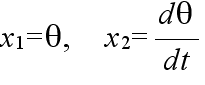
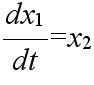
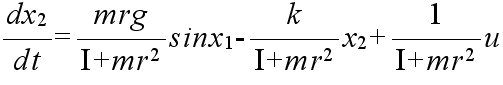
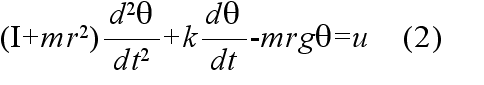
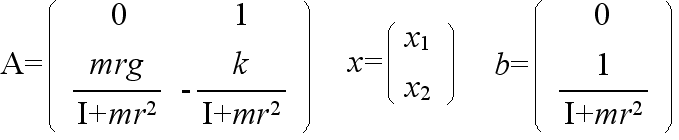
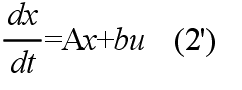
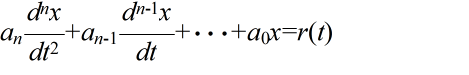
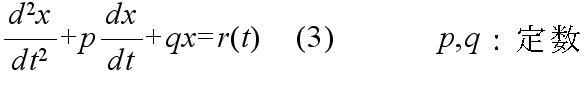
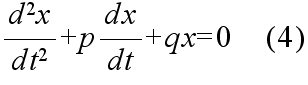
1. (3) 式の一般解は補助方程式 (4) の一般解に，(3) 式の一つの特別解を加えることによって得られる．

2. 補助方程式 (4) の一次的に独立である二つの解を x₁, x₂ とすると
   x = c₁x₁ + c₂x₂

   は (4) の解で，これは (4) の一般解である．従って，(3) 式の特別解を η とすると，

   x = c₁x₁ + c₂x₂ + η

   は，(3) 式の一般解である．

　　そこで，まず，(4) 式の一般解を求める必要があります．(4) 式の解を，

x = e^mt

とおき，(4) 式に代入すると，

m²e^mt + pme^mt + qe^mt = 0

という関係が得られます．e^mt ≠ 0 ですので，

m² + pm + q = 0　　　(5)

となります．この方程式を，特性方程式と呼びます．この方程式は，m の 2 次式ですので，m について解くことができます．一般に，定係数 n 階線形微分方程式に対する特性方程式は，n 次の代数方程式になり，n 個の根を持ちます．その次数が 2 次以下の場合は，簡単に根を求めることができますが，3 次以上のときは，場合によっては，コンピュータを使用して数値的に求める必要があります．

　　(5) 式の根は，p や q の値によって，実根または虚根になります．各場合に対して，(4) 式の一般解の求め方について説明していきます．

1. p² - 4q > 0 の場合　　二つの実根を m₁, m₂ とすると，
   e^m₁t，　e^m₂t
   は，一次的に独立な (4) 式の解となります．従って，(4) 式の一般解は，以下のようになります．

   x = c₁e^m₁t + c₂e^m₂t

2. p² - 4q = 0 の場合　　重根を m とすると，
   e^mt
   は，(4) 式の解となります．今，(4) 式の解を，

   e^mtu
   とおき，(4) 式に代入すると，

   u = c₁t + c₂
   という関係が得られます．この結果，

   e^mt(c₁t + c₂)
   が，(4) 式の一般解となります．つまり，一次的に独立な 2 つの解は以下のようになります．

   x = te^mt，　e^mt

3. p² - 4q < 0 の場合　　二つの虚根を α ± iβ とします．(4) 式の解を，
   e^αtu
   とおき，(4) 式に代入すると，

   u = c₁sinβt + c₂cosβt
   という関係が得られます．従って，(4) 式の一般解は，以下のようになります．

   x = e^αt (c₁sinβt + c₂cosβt)
   　= k₁e^αt sin(βt + k₂)
   ただし，
   　　　　k₁ = (c₁² + c₂²)^0.5
   　　　　cos k₂ = c₁ / (c₁² + c₂²)^0.5

　　1 階や 3 階以上の微分方程式に対しても，全く同じ方法で解くことができます．例えば，1 階の微分方程式の場合は，特性方程式が 1 次の代数方程式になりますので，その根を m₀ とすると，一般解は，

c₀e^m₀t

となります．3 階の微分方程式の場合は，特性方程式が 3 つの根を持ち，一つは実根 m₀，他の 2 つは，2 階の微分方程式の場合と同様，実根又は虚根になりますので，その一般解は以下に示すいずれかの形になります．

x = c₀e^m₀t + c₁e^m₁t + c₂e^m₂t　　　// 3 つの異なる実根

x = c₀e^m₀t + e^mt(c₁t + c₂)　　　// 1 つの実根と 1 つの重根

x = e^m₀t(c₀t² + c₁t + c₂)　　　// 3 重根

x = c₀e^m₀t + k₁e^αt sin(βt + k₂)　　　// 1 つの実根と虚根

　　次に，(3) 式の特別解の求め方ですが，残念ながら，それほど一般的な方法はありません．r(t) の形によって，適当な関数を設定し，必要な係数を決定するという方法が最も一般的です．例えば，下に示す例のように r(t) が定数の場合は定数 k を仮定，t に関する 1 次関数の場合は ( k₁t + k₂ )のような t の 1 次式を仮定，さらに，三角関数のような場合は k₁sin(θt + k₂ ) のように三角関数を仮定して，各係数 k_i を，それらの関数が微分方程式を満足することから決定する方法です．

例1： 微分方程式，

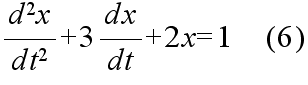
を，初期条件，

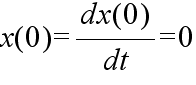
のもとで，解いてみます．特性方程式の解より，補助方程式の一般解は，

x = c₁e^-t + c₂e^-2t

となります．r が定数ですので，(6) 式の特別解を

x = k　　　k : 定数

とおいて，(6) 式に代入し，左辺と右辺の係数を比較することによって k の値を決定すると，k = 0.5 となります．従って，(6) 式の一般解は以下のようになります．

x = c₁e^-t + c₂e^-2t + 0.5

初期条件より，

c₁ + c₂ + 0.5 = 0

-c₁ - 2c₂ = 0

という関係が成立しますので，最終的な解は，以下のようになります．

x = -e^-t + 0.5e^-2t + 0.5

２．２．２ 特性方程式の解とシステムの挙動

　　この節では，特性方程式の解とシステムの挙動について説明します．前節における説明からも明らかなように，特性方程式の根が実数となる場合，いずれかの根が正になると，x の値は無限大に発散してしまいます．また，虚根の場合は，αの値が正の場合に同様の現象が発生します．従って，安定した（無限大に発散しない）システムであるためには，特性方程式の根におけるすべての実部が負である必要があります．

　　システムが安定であれば，時間の経過と共に，システムは微分方程式から決まる何らかの状態に収束していきます．特性方程式の根が実根の場合は，振動せず，収束していきます（下の左図）．また，虚根の場合は，振動しながら，収束していくことになります（下の右図）．

　　ここで，行列の固有値との関係を考えてみます．

とおくと，(3) 式は，

のように書き表せます．行列 A の固有方程式は，

λ² + pλ + q = 0

となり，特性方程式 (5) と一致します．このように，線形システムの挙動は，行列 A の固有値によって決まってきます．

２．３ シミュレーション（微分方程式の数値解）

　　前節においては，線形微分方程式の解析解を求める方法について説明しました．しかし，倒立振り子の例でも示しましたように，ほとんどのシステムの微分方程式モデルは非線形になると言っても過言ではありません．それを線形化したモデルで十分な場合は問題ありませんが，どうしても非線形微分方程式を解かざるを得ない場合が存在します．

　　そのような場合，コンピュータを使用して数値解を求める（コンピュータ上でシステムをシミュレーションする）必要があります．その際，最もよく使用されるのが，ルンゲ・クッタ法です．

　　C/C++ によるプログラム例は，(1) 式を解くためのものであり，各パラメータは以下のようになっています．(1) 式が，1 階の連立微分方程式に変換されて解かれていることに注意してください．なお，ルンゲ・クッタ法内に記述してある JavaScript 版を使用して，画面上で解を求めることも可能です．　→　

m : 10.0

r : 0.5

k : m

u = -k₁θ　　ただし，k₁ = 2 m r g

　　微分方程式を解く際，特に刻み幅（プログラムにおける h の値）に注意してください．刻み幅が，大きすぎると，ルンゲ・クッタ法の箇所で説明したように，正確に微分方程式を解けなくなります．しかし，余り小さくすると，丸め誤差のためかえって精度が悪くなったり，または，計算時間がかかりすぎたりします．

２．４ 具体例

　　ここでは，具体的な例に基づき，システムの挙動についてもう少し詳しく見ていきます．

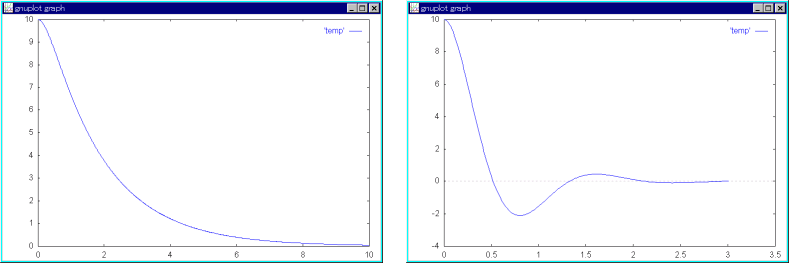
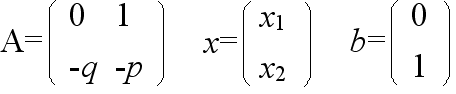
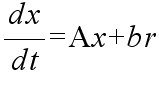
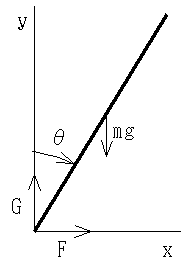
1. 剛体振り子
   　　右図に示すような剛体振り子について考えてみます．このシステムに対する微分方程式は，倒立振り子の場合と同様にして，簡単に求めることができ，以下のようになります．
   
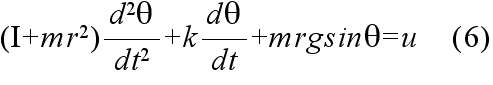
   また，この式を，θ = dθ/dt = 0 の近傍で線形化すると以下のように成ります．
   
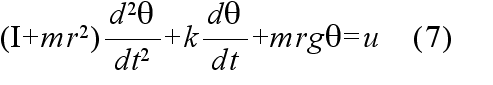
   なお，以下の検討において，各パラメータは，次のように設定します．

   m : 1.0
   r : 0.5
   u = -k₁θ

   　　まず最初に，k = -k₁ = 0 の場合について考えます．この場合，摩擦がありませんので，棒をある角度まで持ち上げ，そこで手を離せば，永久に振動し続けるはずです．実際，線形化された式 (7) を，θ = 10°， dθ/dt = 0°/s の初期条件の下で解くと，

   θ = 10.0 cos ( 3.83406 t )

   のようになります．また，非線形の微分方程式 (6) を，ルンゲ・クッタ法によって解くと，下の左図のようになり，上で得られた解析解とほぼ一致します．下図において，左側の図は，刻み幅 h を 0.01 にした場合であり，また，右側の図は，0.3 にした場合です．このように，刻み幅を大きくすると，微分方程式を正しく解くことができません．
   
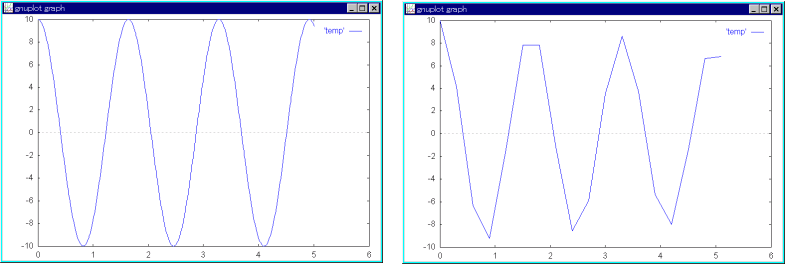
   　　次に，初期条件 θ = 170°， dθ/dt = 0°/s の下で解くと，下の図のようになります．
   
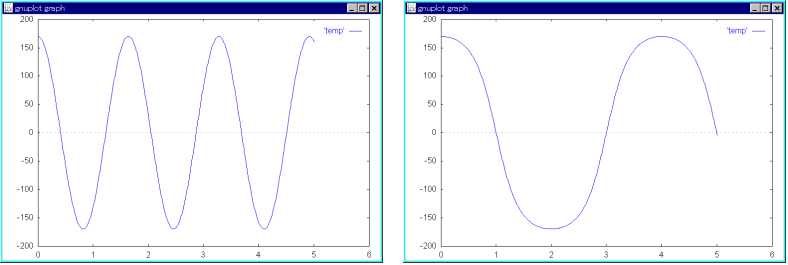
   この図において，左側は線形化された (7) 式，右側は元の微分方程式 (6) 式を解いた結果です．明らかに二つは異なっています．θ = 10° の場合は一致したのに，なぜ，この場合は異なってくるのでしょうか．線形化は，θ = dθ/dt = 0 の近傍 で行われたことを思い出してください．θ = 170° が，θ = 0° の近傍とはみなされないことがこの原因です．

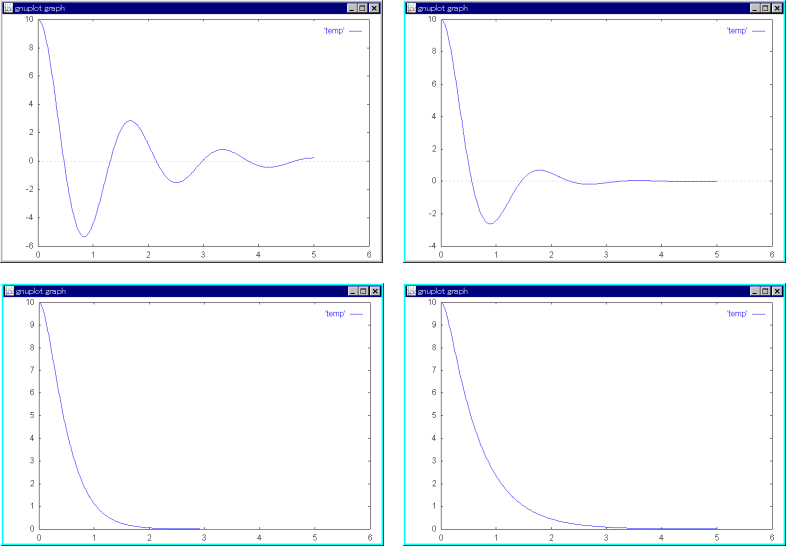
   　　摩擦を増加させる（ k の値を大きくする）と，どのようになるでしょうか．θ = 10°， dθ/dt = 0°/s の状態で手を離せば，永久に振動し続けることなく，いつかは止まってしまうはずです．k の値が小さいときは，振動しながら停止に向かいますが，k の値を大きくすると，振動することなしに停止に向かうはずです．以下は，各 k の値に対して，微分方程式 (7) を解いた結果です．特性方程式の根がどのように変化していくかという点に注目してください．

   k = 0.5　　θ = 10.19700 e-0.75000 t sin (3.75999 t + 1.37391)
   k = 1.0　　θ = 10.86611 e-1.50000 t sin (3.52846 t + 1.16883)
   k = 2.6　　θ = -22.30546 e-4.61414 t + 32.30546 e-3.18586 t
   k = 3.5　　θ = -2.31925 e-8.83643 t + 12.31925 e-1.66357 t			

   下に示すのは，上記の各場合に対する結果を図示したものです（上左：k = 0.5， 上右：k = 1.0， 下左：k = 2.6， 下右：k = 3.5）．特性方程式の根との関係に注目してください．
   
2. 倒立振り子
   　　次に，倒立振り子について検討してみます．剛体振り子の場合と同様，k = -k₁ = 0 の場合について考えます．この場合，摩擦がありませんので，棒をある角度まで持ち上げ，そこで手を離せば，非常に大きい振動幅ですが（ 2 章の最初の図に示したように，剛体振り子の場合と，角度の取り方が異なっている），永久に振動し続けるはずです．

   　　では，線形化された式ではどうでしょうか．線形化された式 (2) を，θ = 10°， dθ/dt = 0°/s の初期条件の下で解くと，以下のようになります．

   θ = 5.0 e3.83406 t + 5.0 e-3.83406 t			

   明らかに，この式は振動を表現していません．また，特性方程式の一つの実根が正（ 3.83406 ）ですので，時間の経過と共に無限大に発散してしまいます．
   
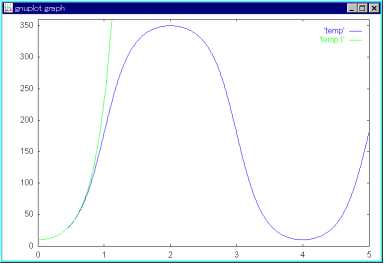
   　　上の図は，線形（緑のグラフ）及び非線形微分方程式を解いたものを一つの図に表したものです．非線形微分方程式を解いた結果は，予想通り，10 度から 350 度の範囲で振動しています．線形微分方程式を解いた結果は，無限大に発散していますが，θ の小さな範囲では，非線形微分方程式の結果とほぼ一致しています．この現象は，線形微分方程式の結果が，時間と共に，線形近似した近傍から遠ざかることによって生じています．

３．待ち行列モデル

　　待ち行列モデルも，先に述べたエレベータシステムだけでなく，電話通信システム，計算機システム，輸送システム（道路，鉄道，航空），工場や機械の保守・サービス，在庫・生産システム等，様々な分野で利用されています．ここでは，待ち行列モデルについて，簡単に説明します．

３．１ 待ち行列

３．１．１ 確率過程

　　待ち行列システムは，一種の確率過程です．そこで，確率過程に関して簡単に説明します．確率過程とは，確率的法則に支配されながら時間と共に経過し変動する現象をいいます．代表的な確率過程としては，以下のようなものがあります．

1. ランダム系列： 時刻 t_n の確率変数 X(t_n) の値が過去や未来の X(t) の値に完全に独立な過程です．つまり，

   P(X1, t1 : X2, t2 : ･･･ : Xn, tn) = Π P(Xk, tk)			

   と表されるような過程です．特に，常に同じ確率の法則に支配されるランダム系列を，ベルヌーイ試行の列と呼びます．

2. マルコフ過程： 時刻 t_n における系の状態は t_n-1 の状態だけで決まるような過程です．つまり，

   P(X1, t1 : X2, t2 : ･･･ : Xn, tn) = P(Xn, tn | Xn-1, tn-1)			

   と表されるような過程です．各時刻において取りうる状態の種類が，

   X = {x1, x2, ･･･, xn}			

   のように有限であり，かつ，遷移確率（ある時刻で状態が x_j であるとき，次の時刻で状態が x_i となる確率），

   P(Xn+1 = xi | Xn = xj) = pij			

   が，時間によらず一定な場合を，有限状態定常マルコフ過程と呼びます．このとき，

   P = [pij]　　　p1j + p2j + ･･･ + pnj = 1			

   を，遷移確率行列と呼びます．

３．１．２ 待ち行列システム

　　以下，下図に示すような待ち行列システムについて検討します．

このシステムは，待ち行列システムとして最も簡単な例です．客が到着すると，窓口が空いていればサービスを受け，空いていなければ唯一存在する待ち行列に並ぶというシステムです．

　　このシステムを表現するのに，以下に示すような，ケンドール記号がよく使用されます．

X / Y / s(N) ： ケンドール記号

X, Y ： 到着分布とサービス分布を表す．分布により，以下の記号を使用する．

• M ： 指数分布
• E_n ： n 相アーラン分布
• G ： 一般分布
• D ： 一定分布

s ： 窓口の数

N ： システムの容量（待ち行列の許容最大長，∞のときは省略可能）

３．１．３ 待ち行列システムの解析

　　物理システムに対して微分方程式を導出したように，待ち行列システムを記述する方程式を導出することについて検討してみます．ただし，任意の待ち行列システムを取り扱うことは不可能であるため，到着分布が母数 λ の指数分布，サービス分布が母数 μ の指数分布に従い，窓口の数が s であり，かつ，システムの容量が無限大であるシステム， M / M / s を対象として考えてみます．

　　到着分布は，母数 λ の指数分布ですので，その確率密度関数と分布関数は以下のようになります．

密度関数　f(x) = λe^-λx　x ≧ 0

　　　　　　　 = 0　　 x < 0

分布関数　F(x) = 1 - e^-λx　x ≧ 0　　x 時間内に客が到着する確率

　　　　　　　 = 0　　　 x < 0

このとき，母数 λ は，到着率（単位時間に到着する平均客数）と呼ばれ，また， 1 / λ は，平均到着時間間隔に相当します．

　　また，サービス分布は，母数 μ の指数分布ですので，その確率密度関数と分布関数は以下のようになります．

密度関数　f(x) = μe^-μx　x ≧ 0

　　　　　　　 = 0　　 x < 0

分布関数　F(x) = 1 - e^-μx　x ≧ 0　　x 時間内にサービスが終了する確率

　　　　　　　 = 0　　　　 x < 0

このとき，母数 μ は，サービス率（単位時間に窓口が処理する平均客数）と呼ばれ，また， 1 / μ は，平均サービス時間に相当します．

　　いま，

p_n(t) : 時刻 t においてこのシステムが状態 n にある確率．ただし，状態 n とは，サービスを受けている客と行列の中で待っている客の数 の和が n である状態をいう．

とおき，p_n(t) に対する方程式を求めてみます．

　　最初に，窓口の数が 1 である場合（M / M / 1）について検討します．Δ 時間内に客が到着する確率（到着時間間隔が Δ 以下である確率），及び，Δ 時間内にサービスが終了する確率は，各分布関数のマクローリン展開から，

F(Δ) = λΔ + o(Δ2)
(Δ) = μΔ + o(Δ2)		

となります．時刻 (t + Δ) において状態 n である確率 p_n(t+Δ) は，以下に示す 4 つのケースに対する各確率を加え合わせることによって得られます．

1. 時刻 t で状態 n にあり，続く時間 Δ で客が到着もせず，立ち去りもしない場合

2. 時刻 t で状態 (n-1) にあり，続く時間 Δ で 1 人の客が到着し，だれも立ち去らない場合

3. 時刻 t で状態 (n+1) にあり，続く時間 Δ で客が到着せず，1 人が立ち去る場合

4. Δ 時間内に 2 人以上の客が到着，あるいは，立ち去る場合

例えば，ケース A の場合に対する確率は次のようになります．

（時刻 t で状態 n にある確率）×（Δ 時間内に客が到着しない確率）×（Δ 時間内にサービスが終了しない確率）
　　= pn(t) (1 - λΔ - o(Δ2)) (1 - μΔ - o(Δ2))
　　= pn(t) (1 - λΔ - μΔ - o(Δ2))		

同様に他の確率も求め，それらを加え合わせることによって，

pn(t+Δ) = (1 - λΔ - μΔ) pn(t) + λΔpn-1(t) + μΔpn+1(t) + o(Δ2)		

という関係が得られます．ただし，状態 0 の場合は，これ以上減ることがありませんから，

p0(t+Δ) = (1 - λΔ - μΔ) p0(t) + μΔp1(t) + o(Δ2)		

となります．Δ → 0 とすることによって，結局，以下の確率微分方程式が得られます．

　　これらが，物理システムに対する微分方程式に対応する式となります．残念ながら，この式を直接解くことはできません．そこで，定常状態（十分時間がたち，システムがある状態に収束した状態）について考えてみます．定常状態では，状態は時間に関係なく一定となり，それを微分したもの（左辺）は 0 となります．従って，以下の関係が得られます．

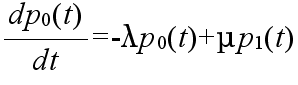
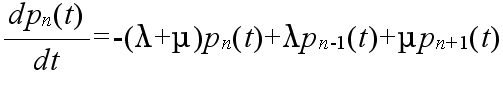
0 = -λp0 + μp1
0 = -(λ + μ)pn + λpn-1 + μpn+1		

上式より，

という関係が得られます．ここで，ρ のことをトラフィック密度（窓口利用率）と呼びます．定常状態になり得るためには，ρ < 1 である必要があります．これは，直感的にも明らかだと思います（単位時間に到着する平均客数が，単位時間に窓口が処理する平均客数より小さい）．

　　また，p_k は確率ですから，

という関係が成立します．したがって，p₀ は，以下のようになります．

p₀ = 1 - ρ

　　窓口の数が s である場合（M / M / s）に対しても，同様に，以下のような確率微分方程式が得られます．

また，ρ や p₀ は，以下のようになります．

　　最後に，以上得られた関係を使用して，待ち行列システムの性質を計算した結果を羅列しておきます．

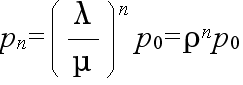
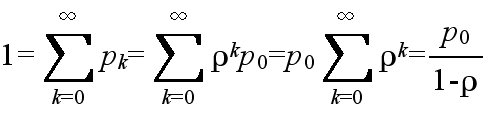
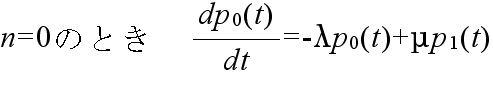
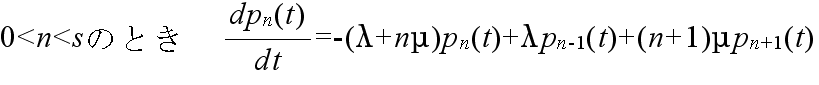
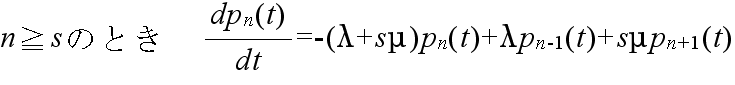
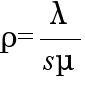
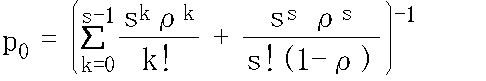
1. 窓口がふさがっている確率： π
   
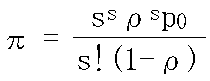
   s = 1 の場合

   π = ρ

2. 平均待ち行列長（サービスを受けている客を除く）： L_q
   
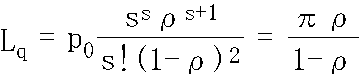
   s = 1 の場合
   

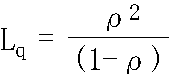
3. 平均系内客数： L
   L = sρ + L_q
   s = 1 の場合
   

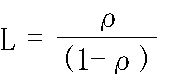
4. 平均待ち時間： W_q
   
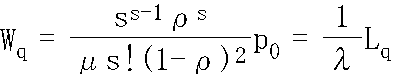
   s = 1 の場合
   

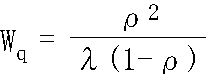
5. システムの平均滞在時間： W
   W = W_q + 1 / μ
   s = 1 の場合

   

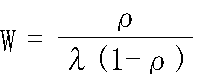
6. t 時間以上待たされる確率
   P(>t) = π e^-(1-ρ)sμt
   s = 1 の場合

   P(>t) = ρ e^-(1-ρ)μt

３．２ 乱数とモンテカルロ法

　　前節において，待ち行列システムの数式モデルについて話しました．しかし，実際上，数式モデルを作成することが不可能である場合がほとんどです．そこで，待ち行列システムの解析手段としては，モンテカルロ法的なシミュレーションに頼る以外方法はありません．そこで，この節では，乱数とモンテカルロ法について説明します．

　　モンテカルロ法とは，乱数を取り扱う技法の総称です．また，乱数とは，ある指定された確率分布を持つ数列であり，計算機では，近似的にランダムな数列を発生させることによって作成します．このようにして生成された乱数を，疑似乱数と呼びます．以後，混乱が起きない限り，疑似乱数を単に乱数と呼ぶことにします．

３．２．１ 乱数の生成

1. 乗算合同法
   　　適当な初期値 x₀ を与え，

   x_i+1 = ax_i　（mod m）

   に従って，系列を計算していきます．この式からも明らかなように，疑似乱数には，必ず周期が存在します（以下に述べる方法においても同様）．つまり，数列を発生していくと，いつか必ず，x₀ に戻ってしまいます．したがって，m， x₀， 及び，a を適当に選択し，できるだけ周期を長くしてやる必要があります．

2. 混合合同法
   　　適当な初期値 x₀ を与え，

   x_i+1 = ax_i + c　（mod m）　　　c と m は互いに素

   に従って，系列を計算していきます．

　　いずれの方法においても，余りを計算しなくてはなりませんが，乱数の品質をそれほど問題にしない場合は，整数演算の性質を使えば，余りを計算せず，非常に簡単に乱数を生成できます（整数が 4 バイトで表現されている場合は，m = 2³¹ となる）．C/C++ によるプログラム例は，[-2³¹, 2³¹] 区間の一様乱数を，混合合同法で生成した例です．　→　

　　　乱数を生成した際，実際には，疑似乱数が十分真の乱数に近いか否かを調べる（乱数の検定を行う）必要がありますが，説明は省略します．

３．２．2 種々の分布に従う乱数

　　以下の説明において，r は，[0, 1] 区間の一様乱数とします．

1. 一様分布

密度関数　　f(x) = 1 / (b - a)　　　a ≦ x ≦ b

　　　　　　　　 = 0　　　　　　　x < a， または， x > b

　　　E[X] = (a + b) / 2

　　　V[X] = (a - b)² / 12

[a, b] 区間の一様乱数の生成方法

x = a + (b - a) r

2. 指数分布

   分布関数　　F(x) = 1 - e^-λx　　　x ≧ 0

   　　　　　　　　 = 0　　　　　　　 x < 0

   密度関数　　f(x) = λe^-λx　　　x ≧ 0

   　　　　　　　　 = 0　　　　 x < 0

   　　　E[X] = 1 / λ = m

   　　　V[X] = 1 / λ²

   指数乱数の生成方法

   x = - m log r

3. 正規分布　N(μ, σ²)

   

   

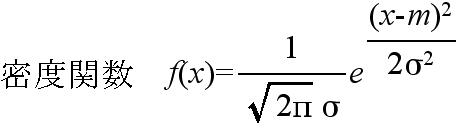
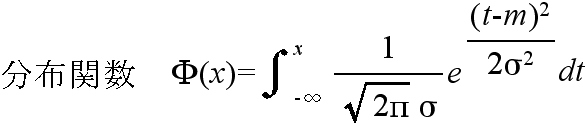
   　　　E[x] = μ

   　　　V[x] = σ²

   　　中心極限定理より，n 個の [0, 1] 区間の一様乱数 r₁, r₂, ･･･, r_n の和は，n が ∞ のとき，平均値 n / 2，分散 n / 12 の正規分布となります．そこで，以下の式によって，N(μ, σ²) の正規乱数を生成します．

   

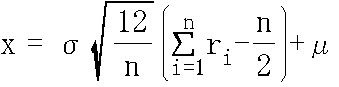
   一般に，n = 12 とする場合が多いと思われます

　　最後に，一様乱数，指数乱数，及び，正規乱数を発生させるC/C++ によるプログラムを提示しておきます．このプログラムにおいては，標準関数の rand を使用していますが，rand は，16 ビットを使用しているためその周期が短く（最大でも，32767 ），あまり質が良い乱数を生成してくれません．そこで，メルセンヌ・ツイスタを使用した例（ MT.h を含む）も添付しておきます．なお，メルセンヌ・ツイスタでは，以下に示すような乱数を生成できます．　→　．

genrand_int32() //符号なし32ビット長整数

genrand_int31() //符号なし31ビット長整数

genrand_real1() //一様実乱数[0,1] (32ビット精度)

genrand_real2() //一様実乱数[0,1) (32ビット精度)

genrand_real3() //一様実乱数(0,1) (32ビット精度)

genrand_res53() //一様実乱数[0,1) (53ビット精度)

　　C++11 で記述可能であれば，メルセンヌ・ツイスタ法を使用した乱数生成関数が，標準ライブラリ内に含まれています．さらに，標準ライブラリ内には，ベルヌーイ分布乱数，二項分布乱数，幾何分布乱数，負の二項分布乱数，一様分布乱数，ポワソン分布乱数，指数分布乱数，ガンマ分布乱数，ワイブル分布乱数，極値分布乱数，正規分布乱数，対数正規分布乱数，カイ二乗分布乱数，コーシー分布乱数，フィッシャーの F 分布乱数，ステューデントの t 分布乱数，確率分布生成器，重み付き確率分布生成器，線形重み付き確率分布生成器を生成する関数も含まれています．他の言語（ JavaScript，PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「乱数の発生」をご覧ください．

　　モンテカルロ法は，様々な分野で使用されます．ここで問題としている確率的な現象を扱う場合に限らず，例えば，多重積分のような確定的な問題にも使用されます．C/C++ によるプログラム例は，乱数を使用して，y = x² を，0 から 1 まで積分するプログラムです．　→　

３．３ 待ち行列問題のシミュレーション

　　微分方程式モデルのように，動的なシステムをシミュレーションする場合は，コンピュータ内部で時間を進めていく必要があります．微分方程式モデルでは，刻み幅という形で，一定時間毎に時間を進めていきました．

　　しかし，待ち行列システムの場合はどうでしょうか．例えば，自動券売機を何台設置すべきかをシミュレーションによって決めたいとします．このとき，時間を進める基本単位である刻み幅をどの程度にすればよいでしょうか．かなり小さくしないと，たくさんの人がほぼ同時に券売機に殺到したような場合に，適切な処理を行うことができません．しかし，誰も来ないときは，システムの状態が変化しないため計算をする必要が無いにもかかわらず，無駄な計算を頻繁に行わなければ成りません．

　　待ち行列システムのように，何か事象（客の到着，サービスの開始・終了等）が発生しない限り状態が変化しないようなシステムを事象駆動システムと呼びます．このようなシステムでは，時間を一定毎に進めず，事象が発生した時点へ次々と時間を進めていく方法がとられます．つまり，次に発生する事象の内，最も早く発生する事象を調べ，その時点まで時間を進め状態の変更等何らかの処理を行うといった方法です．この方法に従い，待ち行列システムをシミュレーションするための基本的な流れを以下に示します．実際のプログラムに関しては，その下に示すプログラム例を参照して下さい．

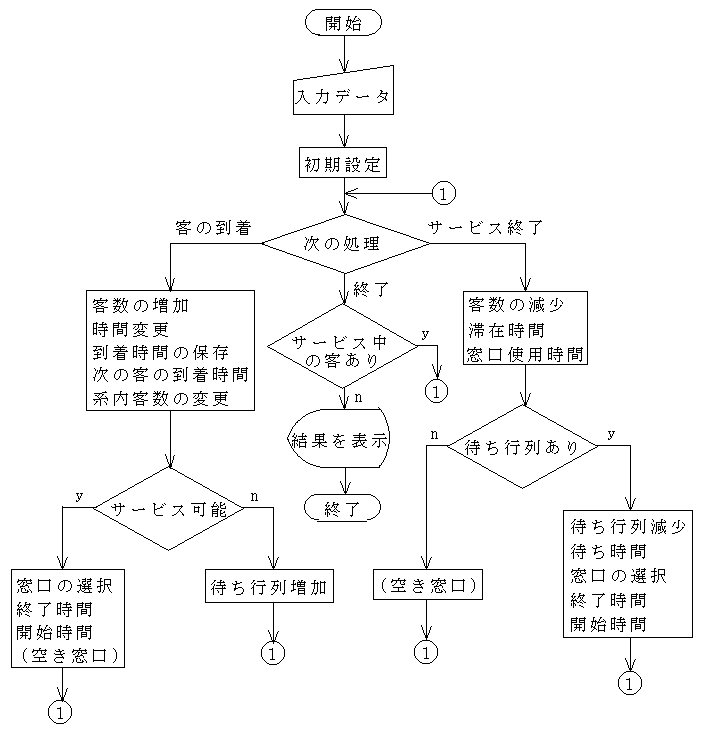
1. 待ち行列が 1 つで，かつ，サービス窓口の数が s であるような非常に簡単な例
   
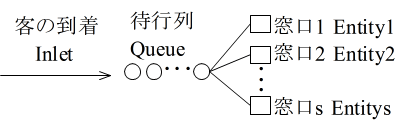
   に対する C/C++ によるプログラム例です．出力結果において，括弧内に書かれた数値は，3.1.3 節で計算された理論値です．到着分布，サービス分布，共に指数分布を仮定していますので，十分長い時間シミュレーションを実行すれば，シミュレーション結果が理論値に近い値になるのが分かると思います．なお，JavaScript 版では，画面上でシミュレーションを実行し，結果を得ることができます． → ，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「待ち行列（簡単な例）」をご覧ください．

2. 次は，図，
   
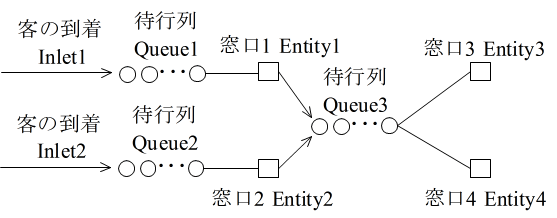
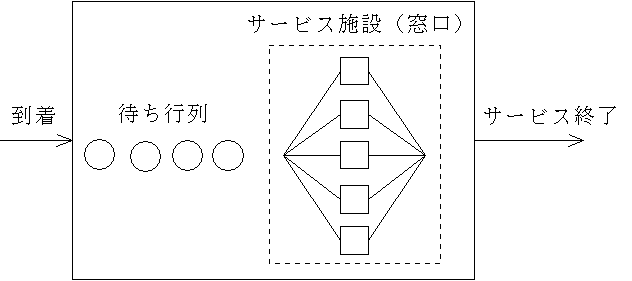
   に示すように，多少複雑な待ち行列問題に対するシミュレーションも可能にした C/C++ によるプログラム例です．入力データによって，様々な構造のモデルに対するシミュレーションが可能です．また，到着時間に関しては，（指数分布，一定時間間隔，客の人数と到着時間の指定）の中から，また，サービス時間に関しては，（指数分布，一定時間）の中から選択可能です．プログラムの最後に，上の図に示したモデルをシミュレーションするための入力例，及び，最初に示した簡単な例に対する入力例が与えてあります． → ，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「待ち行列（複雑な例）」をご覧ください．
   　　JavaScript 版では，画面上でシミュレーションを実行し，結果を得ることができます．初期設定の状態は，上の図に示したモデルをシミュレーションするためのものです．入り口，待ち行列，窓口の数などを変えれば（変更して，その位置に対するフォーカスを外せば)，対応した状態が表示されます．なお，入り口，待ち行列，及び，窓口数の最大値は 10 に設定してありますが，ファイル complex.htm の 11 ～ 13 行目を修正することによって，容易に変更可能です．