　　システムを制御するには，大きく分けて二つの方法があります．フィードフォワード制御：Feedforward Control （開ループ制御：Open Loop Control ）とフィードバック制御：Feedback Control （閉ループ制御：Closed Loop Control ）です．部屋の温度を制御しようとした場合，一日の気温の変化，室内の人数変化，扉の開閉時間・回数などを正確に予測できれば，空調機の運転スケジュールを前もって決めておくことによって部屋の温度を目標とする温度に正確に設定できるはずです．このような制御をフィードフォワード制御と呼び，その概念図は以下のようになります．この図において，制御対象が温度制御をしたい部屋，制御要素が空調機，被制御量が室温に相当します．

　　しかし，この方法では，温度変化や人数変化が予測と異なった場合(システムに外乱が加わった場合)は，目標とする温度を保つことはできません．さらに，設定温度を変更したいような場合は，最初から制御スケジュールを設計し直す必要があります．そこで考えられるのが，現時点における部屋の温度（被制御量）を測定し，その値を制御要素の前まで戻し（フィードバックし），目標値（設定したい室温）と比較し，その差に見合った操作を行ってやる方法です．つまり，室温が目標値より高ければ，空調機に室温を下げるような動作をさせ，逆に低ければ室温を上げるような動作を行わせる方法です．これがフィードバック制御であり，その概念図は以下のようになります．基準入力要素は，目標値を基準入力信号（電流，電圧など，制御要素を操作する信号）に変換する要素，また，フィードバック要素は，被制御量を基準入力信号と比較できる信号に変換する要素です．

　　この章では，基本的に，フィードバック制御を扱います．特に，制御というものを概念的に理解してもらうために，制御理論に関する詳細な説明は省略すると共に，制御システムの解析に重点を置き，制御システムをどのようにして設計するかについてはほとんど触れません．

　　制御に関する詳細な説明に入る前に，もう少し，フィードバック制御の概念的な説明を行っておきます．制御の専門家の方から見れば，多少おかしな説明になるかもしれませんがご容赦ください．制御を行うための基本的な要素として 3 つの要素が存在します．それは，比例要素，微分要素，及び，積分要素です．非常に一般的にいえば，これらの要素を適当に組み合わせて，目的の出力が得られるようにするのが制御であるといえます．各要素の概念的な役割は以下に示すとおりです．

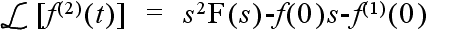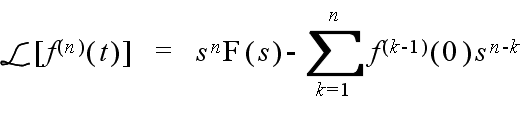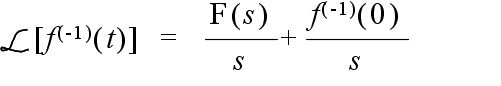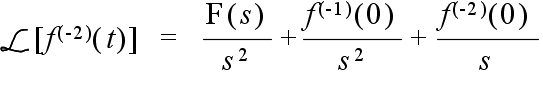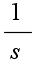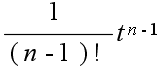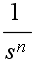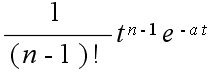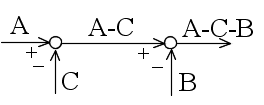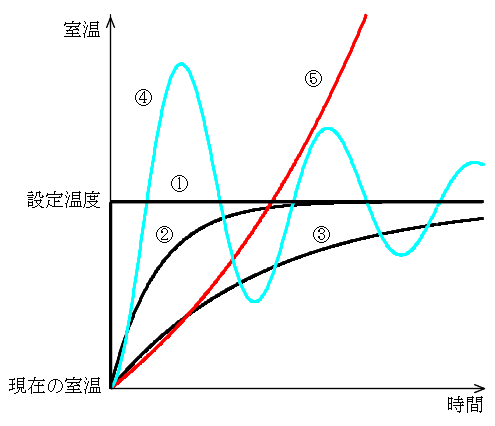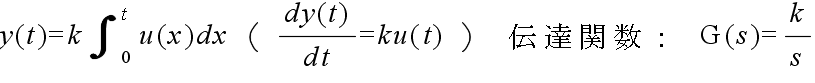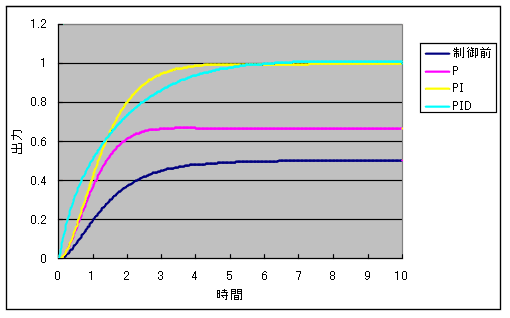
比例要素：　現在の出力値と目標値との間に何らかの差があれば，その差に比例した量に基づいた操作を行うのが最も簡単な方法です．しかし，差が小さすぎて測定できない，差が生じた時点で操作を行っては遅すぎる，などといった問題が生じる場合があります．
微分要素：　「微分積分」の章でも説明しましたように，微分とは予測演算子です．出力の変化率から，「将来は～になるであろうから，前もって，～のような操作を行っておく」といった操作が，微分要素に対応します．予測が的中すれば，非常に良い結果が得られるでしょうが，誤っていた場合は，とんでもない結果（システムが不安定になる）になる可能性もあります．
積分要素：　非常にわずかな水滴（誤差）であっても，それが蓄積（積分）されれば，その量は非常に多くなります．積分要素の基本動作はこの点に基づいています．しかし，この例からも明らかなように，蓄積された後に操作が行われることになりますので，操作を加えるタイミングはどうしても遅れがちになります．遅れが大きければ，システムの安定性を損なうような場合も発生します．

２．制御システムのモデル

２．１伝達関数モデル

　　制御システムを解析・設計するためには，そのモデルが必要になります．「システムのモデルとシミュレーション」の章で述べたように，一般に，物理システムは常微分方程式によって記述可能です．熱の移動に関するシステムのように，偏微分方程式で記述される分布定数系も存在しますが，それらのシステムも，場合によっては，常微分方程式で記述される集中定数系で近似して解析することが可能です．そこで，制御理論においては，主として，常微分方程式で記述されるシステムを対象とします．

　　厳密に言えば，ほとんどの場合，システムは非線形常微分方程式で記述されます．非線形常微分方程式は，その一般解を求めることができないため，解析が非常に困難になります．しかし，興味の対象となる状態の近傍（例えば，部屋の設定温度の近傍）だけを考えれば，定係数線形常微分方程式によって近似することができます．定係数線形常微分方程式の一般解を求めることは可能であり，また，線形システムにおいては，「重ね合わせの理」が成立し，解の導出や解析が容易になります．「重ね合わせの理」とは，システムへの入力が u₁ のときその出力が y₁，入力が u₂ のとき y₂ であったとすると，a，b を定数としたとき，(au₁ + bu₂）の入力に対してその出力は (ay₁ + by₂）となるような性質です．このため，制御理論においては，多くの理論が定係数線形常微分方程式で記述されるシステムを対象としています．この節においても，1 入力 1 出力の定係数線形常微分方程式で記述されるシステムを対象とします．具体的には，システムへの入力を u(t)，出力を y(t) としたとき，次の微分方程式によって記述されるシステムを対象とします．ここで，a₀，･･･，a_n，b₀，...，b_mは定数とします（ n ≧ m ）．

　　線形であるとはいえ，次数が高くなると解を求めることは面倒な仕事になります．そこで微分方程式を直接解くことなく，システムの解析・設計を行う方法として，伝達関数を使った方法がよく使用されます．この節では，微分方程式で表現されたシステムを伝達関数に変換する方法について説明します．伝達関数モデルを利用することによって，微分方程式を代数方程式として取り扱うことが可能になり，解析・設計が容易になります．

２．１．１ラプラス変換

　　ラプラス変換とは，時間領域の関数 f(t) を複素領域の関数 F(s) に変換する操作であり，以下のように定義されます．

ここで，f(t) は，t > 0 で定義される 1 価関数です．上記の変換を，記号的には，

と書きます．勿論，すべての関数に対してラプラス変換が可能なわけではありません．(2.2) 式で示した積分が収束する必要がありますが，制御システムに現れるほとんどの関数がラプラス変換可能であることもあり，詳細な議論は省略します．

　　逆に，F(s) から f(t) への変換は，ラプラス逆変換と呼ばれ，以下のように定義されます．

また，記号的には，

と書きます．以下，ラプラス変換の諸性質，及び，主要な関数のラプラス変換をあげておきます．なお，以下の表において，f⁽ⁿ⁾(t) は，f(t) の n 階微分，f^(-n)(t) は，f(t) の n 重積分を表すものとします．

*表2．１ラプラス変換の諸性質*
名称	性質・定理
線形性
線形性
ｔ領域での微分

	・・・・・

ｔ領域での積分

	・・・・・

スケール変換
ｔ領域での推移定理
ｓ領域での推移定理
たたみ込み積分
初期値定理
最終値定理

*表2．2 主要な関数のラプラス変換*
時間関数 f(t)	複素関数 F(s)
単位インパルス関数 δ(t)	１
単位ステップ関数 u(t)

２．１．２伝達関数とブロック線図

　　伝達関数は，

「すべての初期値を零にしたときの出力信号と入力信号の比」

として定義されます．つまり，システムへの入力信号のラプラス変換を U(s)，出力信号のラプラス変換を Y(s) とすると，システムの伝達関数 G(s) は，以下のようになります．このとき，伝達関数の分母を零とおいた方程式を特性方程式と呼びます．また，分子を零とおいた方程式の根を零点，特性方程式の根を極と呼びます．

例えば，(2.1) 式で表現されるシステムの伝達関数 G(s) は，両辺を，初期値 = 0 としてラプラス変換することによって，以下のようになり，

その特性方程式は，次のようになります．「システムのモデルとシミュレーション」の「微分方程式の解析解」の節で述べた特性方程式と一致していることが分かると思います．

a_nsⁿ + a_n-1s^n-1 + ･･･ + a₀ = 0

　　システムのモデルとして伝達関数が使用されるとき，ブロック線図がしばしば使用されます．ブロック線図は，システム内における信号（情報）の流れを表すものであり，以下に示す 4 つの基本単位で構成されます．回路図などと似ていますが，回路図とは異なり，信号の流れだけを表現し，エネルギー等の流れを表現していないことに注意してください．

基本単位	説明	図
矢印が付いた線分	信号の流れる方向を表します．
ブロック	システム内の要素（サブシステム）を表します．要素の伝達関数を G(s)，入力信号の伝達関数を A(s) とすると，その出力は G(s)A(s) となります．
加え合わせ点	2 つの信号の和，又は，差を生成します．
引き出し点	信号の分岐を表します．分岐により信号の値は変化しないことに注意してください．

　　通常，代表的なフィードバック制御システムは下の左図のようになります．このとき，その右に示す基準入力から出力までの伝達関数，

を閉ループ伝達関数，偏差から偏差までの伝達関数 GH を開ループ伝達関数と呼びます．

　　制御システムが複雑になると，ブロック線図も複雑になります．しかし，以下の性質を利用して等価なブロック線図に変換可能です．

操作	変換前	変換後
引き出し点の交換
加え合わせ点の交換
引き出し点とブロックの交換
加え合わせ点とブロックの交換
ブロックの交換
ブロックの直列結合
ブロックの並列結合
ブロックのフィードバック結合

　　上に述べた性質は，ブロック線図の基本から簡単に導くことができるものです．従って，これらの性質を知らなくてもブロック線図の等価変換を行うことができます．例として，以下に示すブロック線図を等価変換してみましょう．

最初に，上図に示すように，ブロック線図の適当な箇所の信号に名前を付けます（この例では，x と z ）．次に，これらの信号と他の信号との関係を記述します．この例では，以下のようになります．

x = U(s) - G₂z

z = G₁x - Y(s)

Y(s) = G₂G₃z

これらの式から，x 及び z を消去し， Y(s) / U(s) を求めれば，以下のようになります．

２．２状態方程式モデル

２．２．１状態方程式

　　伝達関数モデルでは，1 入力 1 出力システムだけを扱い，また，入力や出力の導関数などを消去しています．しかし，場合によっては，導関数を利用した方がより優れた制御が可能な場合もあります．さらに，一般のシステムにおいては，多入力多出力になり，それらの変数間の相互関係が重要になります．そこで，システムの構造に基づき，その内部状態を使用したシステムの記述が望まれます．それが状態方程式モデルです．

　　一般に，n 次の線形システムの状態方程式は以下のようになります．なお，x の上に書かれた点（「・」）は，時間による微分（ d / dt ）を表しています．これらの式において，x をシステムの状態変数と呼びます．また，(2.5) 式を状態方程式，(2.6) 式を出力方程式と呼ぶ場合もあります．

	x： 状態ベクトル（ n × 1 ）
	u： 入力ベクトル（ p × 1 ）
	y： 出力ベクトル（ m × 1 ）
	A，B，C，D： 行列（各々， n × n， n × p， m × n， m × p ）

　　状態方程式の次元数（状態ベクトルの次元数）は，システムを記述するのに必要十分なものでなくてはなりませんが，状態変数の選び方は唯一ではありません．例えば，(2.1) 式を状態方程式に変換するとき，その次元数は n となりますが，その方法は状態変数の選び方によって異なってきます．ここでは，例として，同伴形式といわれる方法を紹介します．

　　以下，一般性を失うことなく，a_n = 1 とします．また，n > m とします．まず，

を満たす変数を x₁ を一つの状態変数に選択します．残りの状態変数を，

のように選ぶと，状態方程式は以下のようになります．

出力方程式を得るために，(2.7) 式を時間に関して微分します．

(2.9) 式の最初の関係より，この式は以下のようになります．

更にこの式を微分して同様の手続きを繰り返せば u の m 階微分まで計算することができます．その後，それらを (2.1) 式に代入し，左辺と右辺を比較することによって，以下に示す出力方程式を得ることができます．

以上の結果をまとめると，(2.1) 式に対する状態方程式（と出力方程式)は以下のようになります．

なお，n = m の場合は，以下のようになります．

また，ブロック線図は以下のようになります．

２．２．２可制御性と可観測性

　　まず，最初に，次の微分方程式について考えてみます．入力 u として単位ステップ入力を加えたときの解をルンゲ・クッタ法によって求めた結果が上図の一番下の曲線（空色）です．図からも明らかなように，時間と共にある一定値に収束していきます．

　　次に，この微分方程式を，先に述べた方法で状態方程式に変換すると以下のようになります．この状態方程式において，出力だけではなく，状態 x₁，x₂ も表示すると，上図の黄色とピンクの曲線になります．これら 2 つの状態は時間と共に大きくなっています(実際には，無限大に向かう)．

　　このように，この微分方程式においては，観測される出力と内部の状態が大きく異なっています．なぜこのようなことが起きるのでしょうか．先に述べたように，状態の選び方は唯一ではありません．そこで，別の状態を選び状態方程式を書き換え，その様子を見てみます．今，

のような x' を新たな状態に選び直しますと，状態方程式は以下のようになります（ x' を改めて x と置き直しています）．

ここで，T^-1AT，T^-1b，cT を，改めて，A，b，c に置き直しますと，具体的な状態方程式は以下のようになります．

　　この微分方程式を解くと，下図のようになります．当然，出力 y に変化はありません．この図，及び，上の状態方程式からも明らかなように，(2.13) 式で与えられる微分方程式では，出力に上記の状態方程式の状態 x₂ が反映されていません（状態 x₁ を -3 倍した結果だけが出力されている）．つまり，状態 x₂ を外部から観測できないわけです．観測できないことは，場合によっては，大きな問題を引き起こします．この例の場合，もし，状態 x₂ がある箇所の温度や圧力に対応していた場合はどうでしょうか．それらが無限大になってしまうことは大きな問題です．さらに，そのことを観測データから知ることができなければとんでもないことになってしまいます．

　　同様に，状態を入力によって制御できないような場合も存在します．一般に，システムの出力から内部状態を知ることができるとき，そのシステムは可観測（ Observability ）であるといいます．また，任意の初期状態 x₀ から希望する状態 x_d まで入力によって遷移させることができる場合，そのシステムを可制御（ Controllability ）であるといいます．

　　n 次のシステムが可観測であるための必要十分条件は，

が成立することです．実際，例として与えたシステムは，最初の状態方程式において，

となり，可観測ではありません．又，可制御であるための必要十分条件は，

が成立することです．なお，rank は行列の階数を意味しています．

　　次に，可制御性や可観測性について，伝達関数モデルの立場から眺めてみます．(2.13) 式の両辺をラプラス変換して，このシステムの伝達関数を求めると以下のようになります．

この伝達関数 G(s) に対応する微分方程式は，

となり，その解は，(2.13) 式の出力と一致します．なぜこのようなことになるのでしょうか．それは，伝達関数を求める際，この例では，(s-2) の項が分母と分子で消去されてしまうからです．このように，システムが，可制御や可観測でない場合は，分母と分子間で消去が行われます．つまり，伝達関数では，可制御や可観測の部分を表現できない，逆に言えば，システムの中の可制御でかつ可観測な部分だけを伝達関数で表現できることになります．

３．制御システムの特性

３．１システムに要求される特性>

　　例として，部屋の温度を制御する空調システムについて考えてみます．このシステムの場合，まず，「時間がたてば，室温が設定温度に一致する」といったことが当然要求されます．つまり，

1) 十分時間がたてば，被制御量（室温）が目標値（設置温度）に一致する（定常特性）

ことが要求されます．さらに，

2) できるだけ速く被制御量が目標値に一致する（速応性）

ことも要求されます．

　　温度設定を変更すると同時に室温がその温度になる（室温と時間の関係を図示した上図の①）ことが理想ですが，実際にはほとんど不可能です．一般的には，室温は②～④のような形で設定温度に近づいていきます．この中で，②と③を比較すれば，速応性の面からは，③よりも②のように変化することが望まれます．

　　定常特性を満足し，かつ，速応性が良いとはいっても，例えば④のように，大きく振動しながら目標値に近づくような変化はあまり好ましくありません．空調システムの場合で見れば，設定温度は 20 度であるのに，30 度以上の温度になったり，15 度以下の温度になったりということを繰り返しながら設定温度に近づくことは望ましいことではありません．まして，⑤に示すように，室温が時間と共に上昇し続ける（現実には，どこかで止まりますが）ことは論外です．つまり，

3) 時間の経過と共に，定常状態に近づく（安定性）

がシステムに対する最低限の要求になります．実際には，安定であるだけでなく，振動ができる限り速く減衰することが望まれます（減衰性）．

　　制御システムを設計する際には，これら 3 つの特性，定常特性，速応性，及び，安定性を同時に満足させる必要があります．しかしながら，線形制御の範囲では，速応性を良くすれば安定性が悪くなるなど，これら 3 つの特性は競合する関係にあり，それらの妥協点を見つけることになります．システムの特性を見る方法には幾つか存在しますが，ここでは，過渡応答，及び，周波数応答について説明します．

３．２システムの過渡応答

　　システムの特性を見る一つの方法は，システムに何らかの入力を加え，その出力を観察することです．制御理論では，入力として単位インパルス関数や単位ステップ関数がよく使用されます．そして，すべての初期値を 0 としたとき，単位インパルス関数に対する出力をインパルス応答，単位ステップ関数に対する出力をインディシャル応答（単位ステップ応答）と呼びます．ここでは，インディシャル応答に基づいて，システムの特性を見てみます．

３．２．１ラプラス変換と微分方程式の解

　　インディシャル応答を見るためには，まず，微分方程式を解く必要があります．定係数線形常微分方程式の解法については，「システムのモデルとシミュレーション」の「微分方程式の解析解」の節で述べましたが，ここでは，ラプラス変換を使用した方法について説明します．

　　一般に，微分方程式の解は，まず，与えられた微分方程式をラプラス変換し，それを逆変換することによって求めることができます．例えば，(2.1) 式の両辺をラプラス変換すれば，

となります．従って，(2.1) 式の解は，

となります．

　　すべての初期値が 0 の場合は，(3.1) 式は，

となります．表 2.2 から，単位インパルス関数のラプラス変換は 1 ですので，(3.2) 式の右辺は伝達関数に一致します．つまり，伝達関数は，インパルス応答そのものであるといえます．

　　では，具体的に，微分方程式を解く方法について考えてみます．単位ステップ関数のラプラス変換は 1 / s ですので，(3.1) 式は以下のようになります（ b' 等の ' は省いてあります）．

　　従って，(3.3) 式を逆変換することによってインディシャル応答を求めることができます．しかし，このままでは，簡単に逆変換することはできません．そこで，一般的には，(3.3) 式の右辺を部分分数に展開して求めることになります．以下，一般的な議論はかえって理解しにくいかと思いますので，次の微分方程式を対象として説明を進めていきます（ u(t) は，単位ステップ関数）．

(3.4) 式をラプラス変換すると（以下の説明では，初期値は 0 とするが，一般的には 0 でなくても構わない），

となります．従って，(3.5) 式を部分分数に展開しラプラス逆変換すればよいことになります．以下，その方法について説明していきます．

p² - 4q > 0 の場合（特性方程式 s² + ps + q = 0 が異なる 2 実根）

　　s² + ps + q = 0 の 2 つの根を m₁，m₂ とすると，(3.5) 式は以下のように部分分数に展開できます．

表2.1に示したラプラス逆変換の性質より，右辺は各項のラプラス逆変換の和になりますので，表2.2より，インディシャル応答は以下のようになります．

　　k₁～k₃は，(3.6) 式において係数比較を行って求めることもできますが，もっと簡単な方法があります．例えば，上式の両辺に ( s - m₁ ) をかけると以下のようになります．

ここで，s に m₁ を代入すると，右辺は第 2 項及び第 3 項が 0 となり k₁ だけが残りますので，左辺の値が k₁ の値になります．つまり，

の計算を行えばよいことになります（ m₃ は 0 ）．例として，p = 3，q = 2 の場合，k_i の値は以下のようになります．

従って，部分分数に展開した結果は次のようになり，

インディシャル応答は，以下のようになります．
p² - 4q = 0 の場合（特性方程式 s² + ps + q = 0 が重根）

　　s² + ps + q = 0 の重根を m とすると，(3.5) 式は以下のように部分分数に展開できます．

　　k₁ 及び k₃は，先の場合と同様，両辺に，それぞれ，(s-m)² 及び s をかけることによって求めることができます．しかし，k₂ に対しては，(s-m) をかけても．分母に (s-m) が残り，同様の方法では求めることができません．そこで，両辺に (s-m)² をかけたものを s で微分すると，以下のようになります．

このように，右辺の k₁ の項はなくなり，k₂ と k₃ の項が残ります．しかし，s に m を代入すると，k₃ の項は 0 となり，右辺は，k₂ だけとなります．つまり，k₂ は，

の計算によって求めることができます．なお，3 重根以上の場合も同様の考え方で求めることができます．以下，例として，p = 2，q = 1 の場合，k_i の値は以下のようになります．

従って，部分分数に展開した結果は次のようになり，

インディシャル応答は，以下のようになります．
p² - 4q < 0 の場合（特性方程式 s² + ps + q = 0 が虚根）

　　基本的に，2 実根の場合と同様の方法で計算可能です．ただし，計算はかなり面倒になりますので，表2.2 のようなラプラス変換表を用いた方が簡単だと思います．例として，p = 1，q = 1 の場合，表 2.2 の最後の公式を使用すると，インディシャル応答は以下のようになります．

なお，この場合，特性方程式の根は以下のようになり，

指数関数の t の係数はα，三角関数の t の係数はβとなっています．

３．２．２特性方程式の根とシステムの特性

　　以上述べたインディシャル応答からも明らかなように，システムが時間の経過と共に定常状態に近づくためにはインディシャル応答の指数関数における t の係数が負である必要があります．逆に，負であれば時間の経過と共にそれらの項は 0 となり，定常状態に近づいていきます．従って，システムが安定であるための必要十分条件は，

「特性方程式のすべての根の実部が負である」（状態方程式で表現された場合は，(2.5) 式における「行列 A のすべての固有値の実部が負である」）

ことになります．しかし，特性方程式の次数が高くなると，特性方程式の根を求めることは容易ではありません．そこで，次節において，特性方程式の根を求めることなくシステムの安定判別を行う方法について述べます．

　　システムの速応性も，特性方程式の根によって決まってきます．つまり，根の実部の絶対値が大きいほど，指数関数の項は急速に 0 に近づきますので，速応性が良いことになります．

　　システムが安定であれば，時間の経過と共に指数関数の部分は 0 となり，定常状態に近づいていきます．微分方程式を解けば，その状態を知ることは容易ですが，表 2.1 に示した最終値定理を使用すれば，微分方程式を解くことなくその状態を知ることができます．例えば，先に示した例(入力は単位ステップ関数)では，以下のようになります．なお，一般的には，入力信号が一定値であるとは限りませんので，一定速度入力や一定加速度入力に対する性質も重要になりますが，ここでは省略します（以下においても同様)．

　　一般には，微分方程式の特定の係数や特性方程式の特定の根だけを動かすことは不可能です．通常，システム内の変更できるパラメータを修正すれば，微分方程式全体が影響を受けます．そこで，まず最初に，下に示す二次の例を使用して，パラメータの変化によって，システムの特性がどのように変化するのかを見てみます．

　　このシステムにおいて，K の値を変化させると，特性方程式（ s² + 3s + 1 + k = 0 ）の根は，以下のように変化します．

K	特性方程式の根
0.5	2 実根（ -2.37, -0.63 ）
1.0	2 実根（ -2.0, -1.0 ）
2.0	虚根（ -1.5 ± j 0.87 ）
10.0	虚根（ -1.5 ± j 2.96 ）

　　また，インディシャル応答は，K の値により，下図のように変化します．このシステムの定常値は k / (1 + k) ですので，図からも明らかなように，K を大きくすればするほど定常特性は改善されていきます．また，速応性についても同様です．しかしながら，K を大きくするに従って，振動が激しくなってきます．

　　次に，下に示す三次の例を使用して，パラメータの変化によって，システムの特性がどのように変化するのかを見てみます．

　　このシステムにおいて，K の値を変化させると，特性方程式（ s³ + 6s² + 11s + 1 + k = 0 ）の根は，以下のように変化します．

K	特性方程式の根
5.0	3 実根（ -1.0, -2.0, -3.0 ）
10.0	1 実根＋虚根（ -3.90, -1.05 ± j 1.31 ）
20.0	1 実根＋虚根（ -4.60, -0.70 ± j 2.02 ）
50.0	1 実根＋虚根（ -5.65, -0.17 ± j 3.00 ）
100.0	1 実根＋虚根（ -6.64, 0.32 ± j 3.89 ）

　　また，インディシャル応答は，K の値により，下図のように変化します．このシステムにおいても，K を大きくすればするほど定常特性は改善されていきますが，K = 100 の場合に見るように，ついには不安定になってしまいます．

３．２．３安定判別

　　安定判別法には様々なものが存在しますが，ここでは，フルビッツの方法について説明します．今，システムの特性方程式が，

a₀sⁿ + a₁s^n-1 + ･･･ + a_n-1s + a_n = 0　　(3.7)

の形で与えられているものとします．このとき，次の 2 つの条件を満たすときシステムは安定になります．

すべての係数 a₀, a₁, ･･･ ,a_n が 0 でなく，同符号となること
次のフルビッツ行列式 H_i のすべて（ i = 1, 2, ･･･, n-1 ）が 0 でなく，同符号となること

　　例として，次の 2 つのシステムの安定判別を行ってみます．

1) s³ + 6s² + 11s + 6 = 0　　根： -1, -2, -3
2) s⁴ + s³ + s² + 11s + 10 = 0　　根： -1, -2, 1 ± j2

いずれのシステムも，すべての係数は正ですので条件 A は満たされています．そこで，フルビッツの行列式を計算してみます．まず，最初のシステムに対しては，

となり，安定となります．2 番目のシステムに対しては，

となり，不安定となります．

３．２．４状態方程式の解

　　(2.5) 式で与えられた状態方程式の両辺をラプラス変換すると以下のようになります．

従って，

となり，これを逆変換すれば過渡応答が得られますが，詳細については省略します．なお，

は遷移行列と呼ばれ，以下の性質を持っています．

３．３システムの周波数応答

３．３．１周波数応答

　　一般に，システムの出力は，インディシャル応答の場合と同様，過渡応答と定常応答の和で表現されます．システムが安定であれば，十分時間が経過した後には，過渡応答の部分は 0 となり，定常応答の部分だけが残ります．線形システムに対して正弦波信号を付加すると，その定常応答も同じ周波数の正弦波信号となります．例えば，一次のシステム，

に正弦波信号を加えた場合について考えてみます．この場合の微分方程式は，

となり，その出力を求める（微分方程式を解く）と以下のようになります．最初の項（ c は初期状態で決まる定数）が過渡応答であり，時間と共に 0 になっていきます．定常応答の部分を見ると，周波数は入力信号と同じで，振幅と位相だけが異なっています．

　　また，一般に，任意の信号は各種の周波数の正弦波信号の和として表現できます．そこで，各種の周波数の正弦波信号に対するシステムの定常応答からシステムの特性を見て，解析設計を行おうとするのが周波数応答法です

　　しかし，システム毎に微分方程式を解くことは大変な作業です．そこで，上の例において伝達関数の s に jω を代入した複素数，

について考えてみます．すると，G(jω) の絶対値（以下，ゲインと呼びます）と位相は，下に示すように，先に求めた出力の A 及び Φ と一致します．詳細については省略しますが，このように，伝達関数の s に jω を代入することによって，出力信号のゲインと位相が求まる，つまり，微分方程式の定常解が求まることになります．

３．３．２ボード線図

　　横軸に角周波数 ω を対数目盛でとり，縦軸にゲイン |G(jω)| の対数値 20 log₁₀|G(jω)|（単位：デシベル ( dB ) ），及び，位相 ∠G(jω) （単位：度）をとって表示したグラフをボード線図と呼びます．特に，角周波数とゲインを表示したグラフをゲイン線図，角周波数と位相を表示したグラフを位相線図と呼びます．例えば，(3.9) 式で示したシステムのボード線図は以下のようになります（青い線．ピンクの折れ線については後ほど説明します）．

　　このボード線図から以下のようなことが分かります．低い周波数の正弦波に対しては，位相は少し遅れますが，ほぼ同じ振幅の正弦波が出力されます．しかし，周波数が高くなると，出力信号の振幅は急激に小さくなっていきます．つまり，高い周波数の信号ほどこのシステムを通過できない，高い周波数の信号には応答できない，つまり，高い周波数を多く含む速い動作には対応できないことを意味しています．ちなみに，ω → 0 の低周波ゲインより 3 ｄB 低下する周波数をカットオフ周波数と呼びますが（この例の場合は，ω = 1 ），カットオフ周波数が高いほど速応性が良くなることになります．

　　一般に多くの物理システムがこのボード線図のような性格を持っています．例えば，自分の右手をまっすぐ前に突き出し一定のリズム（周波数）で上下に動かしてみてください．この場合，脳から出る信号が基準入力信号，腕の動きが出力になります．ゆっくり動かしている間は，自分の思ったとおりの動きができるはずです．しかし，動きを速くすると，徐々に同じ振り幅（振幅）を維持できなくなるはずです．勿論，この場合は，線形システムでもありませんので全く同じにはなりませんが，上記のゲイン線図と同様の傾向が感じ取れるはずです．

C/C++ により，伝達関数からボード線図を作成するのに必要なゲインと位相を計算するためのプログラム例　→　: Java 版や JavaScript 版では，グラフを表示し，グラフの色や線の太さを変更することが可能です．JavaScript 版では，式の数（グラフの数）や次数に制限をかけていますが（最大の式の数：5，最大次数：10 ），プログラム内の変数 max_g や max_order の値を変えることによって容易に変更できます．なお，他の言語（ PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「ボード線図」をご覧ください．

　　ボード線図がしばしば使用される理由の一つとして，ボード線図の描きやすさがあります（正確なボード線図の計算方法については上に示したプログラム例を参考にしてください）．描きやすさの理由の一つは，

20 log₁₀|G₁(jω)G₂(jω)| = 20 log₁₀|G₁(jω)| + 20 log₁₀|G₂(jω)|
∠G₁(jω)G₂(jω) = ∠G₁(jω) + ∠G₂(jω)

のように，伝達関数の積が和の形で表現できることにあります．また，特にゲイン線図に関しては，直線によって近似的に描いた図と正確な図との差が小さいこともその理由となっています．例として，上であげた (3.9) 式について考えてみます．ω << 1 の範囲では，

G(jω) ≒ 1

と近似できますので，

20 log₁₀|G(jω)| ≒ 0　　∠G(jω) ≒ 0 度

となります．さらに，ω >> 1 の範囲では，

と近似できますので，

20 log₁₀|G(jω)| ≒ 20 log₁₀1 - 20 log₁₀ω = -20 log₁₀ω　　∠G(jω) ≒ -90 度

となります．ゲインは，log₁₀ω を一つの変数とみなせば（ボード線図の横軸），傾きが -20 / デカードの（ 10 倍になる毎に -20 デシベル下がる）直線になります．そこで，この直線と，ω << 1 の範囲の直線（一定値 : 0 ）とを，ω = 1 の箇所で接続したのが，先のゲイン線図中に示したピンクの折れ線です．直線で近似したゲイン線図と正確なゲイン線図の差が最も大きくなるのは ω = 1 （カットオフ周波数）のときですが，その差は 3 デシベルに過ぎません．

３．３．３周波数応答とシステムの特性

　　以下に示すのは，3.2.2 節で例に挙げた二次のシステムに対するボード線図です．いずれも，K の値が小さい場合が下（左）のグラフになっています．定常特性は，ω → 0 の部分に対応しますが，K の値が大きいほど定常特性が改善されている（ゲイン線図において 0 dB に近づいている）のが分かるかと思います．インディシャル応答と比較すると，カットオフ周波数が高いほど速応性が良くなっています．また，ω = 1 付近のピークは，システムが振動し，その値が基準入力信号より大きくなっている（オーバーシュートしている）ことに対応します．

　　以下に示すのは，同じ節であげた三次のシステムに対するボード線図です（ K = 100 の不安定となる場合は除く）．二次のシステムと同様のことが言えます．インディシャル応答と比較してみてください．

　　では，安定性についてはどうでしょうか．三次のシステムの開ループ伝達関数，

のボード線図は以下のようになります．ゲイン線図（上の 5 つのグラフであり，上から，K の値が 100，50，20，10，5 ）と位相線図（一番下のグラフ）が同じ図に描かれているため，縦軸の単位は dB または度となります．ゲインが 0 dB を切る周波数における位相の -180 度との差を位相余有，位相が -180 度を切る周波数におけるゲインの 0 dB との差をゲイン余有といいます．図中に黒の点線と矢印で K = 5 の場合に対する位相余有とゲイン余有（いずれも，矢印の向きが正），また，赤の点線と矢印で K = 100 の場合に対する位相余有が描かれています．この位相余有とゲイン余有が共に正の時システムは安定になります．図からも明らかなように，K = 100 の場合は，いずれの値も負となり，不安定であることが分かります．

　　次に，なぜこのようになるかを概念的に説明してみます．ゲイン余有が正であるとは，対応する周波数に対して，ブロック線図，

における信号 y(t) の振幅が信号 z(t)の振幅より小さくなり（このときのゲインが，0 dB，つまり，1 倍より小さいため），位相が 180 度遅れる（正弦波であれば，符号が逆になる）ことを意味しています．従って，システムに対して，開ループ伝達関数を通過した後の位相が 180 度遅れるような信号を半波長分だけ入力すると，信号 z(t) は以下のように変化します．

このように，ゲイン余有が正であれば，信号 z(t) は時間と共に減衰し，0 になっていきます．しかし，ゲイン余有が負であれば，信号 y(t) の振幅が信号 z(t)の振幅より大きくなるため（このときのゲインが，0 dB，つまり，1 倍より大きいため），同じ信号を入力した場合，以下に示すように z(t) は時間と共に大きくなっていきます．つまり，不安定になるわけです．

４．制御システムにおける基本要素

　　この章では，制御システムの解析・設計の際に重要となる基本的な構成要素の性質について説明します．

４．１比例要素

　　入力信号 u(t) と出力信号 y(t) の関係が

y(t) = ku(t)　　伝達関数： G(s) = k

によって表される要素を比例要素といいます．入力信号が k 倍されて出力される要素であり，そのインディシャル応答や伝達関数は明らかだと思います．

４．２積分要素

　　入力信号 u(t) と出力信号 y(t) の関係が

によって表される要素を積分要素といいます．積分要素のインディシャル応答は

y(t) = kt

となり，k = 1（下），及び，k = 10（上）の場合に対するボード線図は以下のようになります(位相はいずれの場合も -90 度)．

４．３微分要素

　　入力信号 u(t) と出力信号 y(t) の関係が

によって表される要素を微分要素といいます．微分要素のインディシャル応答は

y(t) = kδ(t)　　δ(t)： 単位インパルス関数

となり，k = 1（下），及び，k = 10（上）の場合に対するボード線図は以下のようになります(位相はいずれの場合も 90 度)．

４．４一次遅れ要素

　　入力信号 u(t) と出力信号 y(t) の関係が

によって表される要素を一次遅れ要素といいます．一次遅れ要素のインディシャル応答は，例えば，a = b = 1 で T = 1，及び，T = 10 の時は，
y(t) = 1 - e^-t/T

となり，T = 1（上），及び，T = 10（下）の場合に対するボード線図は以下のようになります．

４．５二次遅れ要素

　　入力信号 u(t) と出力信号 y(t) の関係が

によって表される要素を二次遅れ要素といいます．二次遅れ要素のインディシャル応答は，ω = 1 とすると，

となり，ζ = 2（下），ζ = 1（中），及び，ζ = 0.25（上）の場合に対するボード線図は以下のようになります．

４．６むだ時間要素

　　入力信号 u(t) と出力信号 y(t) の関係が

y(t) = u(t - L)

によって表される要素をむだ時間要素といいます．むだ時間要素は，時間 L だけ出力が遅れる要素であり，そのインディシャル応答は

となり，そのボード線図は，L = 1 の場合，以下のようになります．

４．７ PID 制御

　　制御設計の中でしばしば使用される方法として PID 制御があります．PID は，各々，

P : Proportinal

I : Integral

D : Differential

の略であり，比例，積分，微分を意味します．そこで，PID 制御とは，比例要素，積分要素，及び，微分要素を適当に組み合わせて使った制御方法を意味します．ここでは，3.2.2節でも使用した簡単な例，

を用いて，各要素による制御の影響を見てみます．まず，制御を全く加えないときのインディシャル応答は下に示す図の一番下のグラフになります．

　　まず，定常特性や速応性を改善するために，比例要素だけを使用した P 制御

を行ってみます．その結果が，先に示した図のピンクのグラフになります．なお，K₁ = 2.0 としています．さらに，K₁ を大きくすれば定常特性や速応性は改善されますが，振動が激しくなってしまいます．

　　P 制御では，現在の偏差に比例した制御を行いますが，偏差が小さくなると制御量も小さくなり，十分な効果を発揮できなくなります．また，単に比例定数 K₁ を大きくすれば安定性や減衰性が損なわれる可能性があります．しかし，たとえ偏差が小さくても，それを積分した値は時間と共に大きくなっていきます．そこで，過去のデータの積分（累積）に比例した制御を行おうとするのが積分要素です．次に，比例要素と積分要素を利用した制御，PI 制御，

を行ってみます．その結果が，先に示した図の黄色のグラフになります．なお，K₂ = 0.75 としています．K₂ の値を大きくしていくと，速応性は改善されますが，振動が激しくなり，さらには，不安定になってしまいます．

　　最後に，PID 制御，

を行ってみます．その結果が，先に示した図の空色のグラフになります．なお，K₃ = 1.0 としています．では，微分要素はどのような働きをするのでしょうか．微分要素は，変化率に比例した制御を行います．この例の場合，偏差の変化率が大きいときは，その後偏差が急激に大きくなることを予想して，大きな制御量を出力することになります．上で示したインディシャル応答において，初期の立ち上がりが速くなっている（速応性の改善）のはこのためです．

　　以上のように，比例要素が現在の値に基づいた制御，積分要素は過去の値に基づいた制御，また，微分要素は未来の値に基づいた制御であるとも言えます．積分要素は，過去のデータに基づいているため，必ず制御のタイミングが遅れてきます．一般に，遅れが大きくなるほど，制御しにくく，かつ，不安定になりやすくなります．それを補償するのが，将来を予測した制御を行う微分要素であり，PID 制御は，現在，過去，未来のデータを上手に利用した制御であるといえます．

情報学部

菅沼ホーム

SE目次

索引