情報学部 菅沼ホーム SE目次 索引

システムの最適化

－ １．線形計画法（ LP: Linear Programming ） －

（プログラム例　→　）　：　使用方法

（他の言語（ JavaScript，PHP，Ruby，Python，C#，VB ）によるプログラム例に関しては，「プログラミング言語の落とし穴」第 9 章の「最適化（線形計画法）」をご覧ください）
    1. １．１ 図による解法
    2. １．２ 単体法（シンプレックス法）
    3. １．３ 単体表の使用
    4. １．４ 基底可能解の求め方
　　先に述べましたように，線形計画法（ LP: Linear Programming ）で扱うのは，目的関数，制約条件共に，すべて線形式で成り立っている場合です．つまり，

目的関数，

f(x) = cTx,　　c：n×1, x：n×1　　　(1)

を，制約条件，

Ax ≦ b,　　A：m×n，x：n×1，b：m×1　　　(2)

のもとで，最大にする．

のような問題を扱います．
１．１ 図による解法

　　線形計画法の例として，以下の問題を考えてみます．

［例1.1］ ある製品 A 及び B を生産するためには，3 種類の原料 a，b，及び，c を必要とする．各製品 1 単位を生産するために必要な各原料の量，及び，各原料の現在庫量は以下の表に示す通りとする．また，各製品 1 単位を売却すると，各々，3 及び 2 万円の利益が得られるものとする．利益を最大にする各製品の生産量を決定せよ．
原料 製品 A に対する必要量 製品 B に対する必要量 在庫量
a 3 1 9
b 2.5 2 12.5
c 1 2 8
　　各製品の生産単位を，それぞれ，x1 及び x2 としたとき，この問題を式で表現すると，以下のようになります．

目的関数，

z = 3x1 + 2x2　　　(1)

を，制約条件，

3x1 + x2 ≦ 9　　　(2)
2.5x1 + 2x2 ≦ 12.5　　　(3)
x1 + 2x2 ≦ 8　　　(4)
x1， x2 ≧ 0

のもとで，最大にする．

　　制約条件を満足する領域を図示すると，下図の斜線部分のようになります．したがって，目的関数は，赤線の位置で最大になります．つまり，x1 = 2，かつ，x2 = 3 のとき，最大値 12 となります．
１．２ 単体法（シンプレックス法）

　　前節で述べたように，例1.1 の解は，図を描くことによって簡単に求めることができます．しかし，変数の数が 3 以上になると，図を描くことがほとんど不可能になります．

　　図を使用した解法からも直感的に明らかなように，最大値は，目的関数が制約条件式のいずれかの交点を通るときに得られます．従って，制約条件式が生成するすべての交点に対して，目的関数が各交点を通るときの z の値を調べれば必ず解が得られるはずです．しかし，例1.1 のような簡単な例でさえ，多くの交点が存在します．

　　そこで，交点を調べる作業を効率的に行うようにした方法が以下に述べる単体法（シンプレックス法）です．単体法のアルゴリズムを，例1.1 を使用しながら説明していきます．

  1. 制約条件式を等式に変換するため，スラック変数 x3，x4，及び，x5 を導入し，問題を書き換えます．
    最大： z = 3x1 + 2x2　(1)
    　　 3x1 + x2 + x3 　 　 = 9 　 (2)
    　　 2.5x1 + 2x2 　 + x4 　 = 12.5 　 (3)
    　　 x1 + 2x2 　 　 + x5 = 8 　 (4)
    x1, x2, x3, x4, x5 ≧ 0　(5)
  2. 式(2)～(4)では，3 つの方程式に対して 5 つの変数が存在します．従って，任意の 2 つの変数を 0 とすれば，一意解を得ることができます．この解を基底解と呼びます．さらに，すべての変数がすべての制約条件を満たしていれば（可能解），そのような解を基底可能解と呼びます．このとき，0 とおいた変数を非基底変数，その他の変数を基底変数と呼びます．

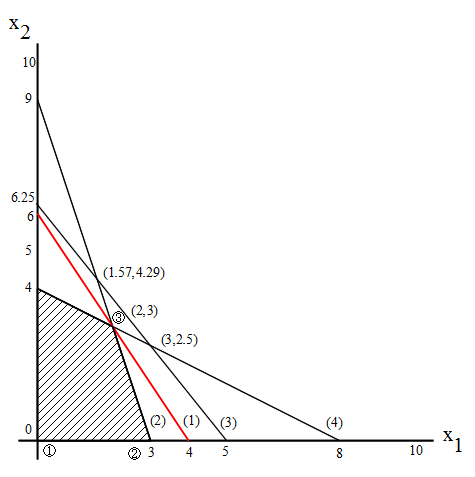
    　　まず，最初のステップとして，基底可能解を見つけます．どのような基底可能解でも良いのですが，一般的に，式を見て直感的に見つかる解を利用します．例えば，この例において，x1 = 0，x2 = 0 （x3 = 9，x4 = 12.5，x5 = 8） は，明らかに基底可能解であり，そのときの目的関数の値 z は 0 となります．（図の交点：①）

  3. 現在の解が最適解か否か，つまり，z = 0 より最適な解は存在するか否かを調べます．式 (1)～(4) より，x1，または，x2 を 1 だけ増加させても，制約条件を侵しませんし，また，目的関数の値は増加します．したがって，現在の解は最適解ではないことになります．

  4. 最適解でないことが分かりましたので，解を改良します．(1) 式の係数の関係から，同じ量だけ増加させる場合，x2 を増加させるよりも，x1 を増加させる方が目的関数の増加量は大きくなります．そこで，x1 を α だけ増加させることにします．もちろん，増加させることによって制約条件 (2)～(4) を侵すことは許されませんので，最大限増加させた場合において，以下の式を満足する必要があります． 
    3 * α + x3 = 9     ∴ x3 = 9 - 3 * α
2.5 * α + x4 = 12.5     ∴ x4 = 12.5 - 2.5 * α
α + x5 = 8     ∴ x5 = 8 - α
    制約条件 (5) より，これら 3 つの変数の値は 0 以上である必要があります．従って，3 つの変数の値が 0 以上になる最大の α の値は 3 となります．明らかにこれも一つの解（x1 = 3, x2 = 0, x3 = 0, x4 = 5, x5 = 5）であり，目的関数の値 z は 9 となります．（図の交点：②）

  5. 再び，現在の解が最適解か否かを調べます．変数 x2 と x3 の値が 0 ですので，x2，または，x3 を増加させることによって，目的関数の値が増加するか否かを調べます．そのためには，目的関数を，x2 と x3 を使用して書き直す必要があります．そこで，α = 3 を導出した式 (2) を使用し，他の式から x1 を削除します．
    最大： z = 9 + x2 - x3　(6)
    　　 3x1 + x2 + x3 　 　 = 9 　 (7)
    　　 (3.5 / 3)x2 - (2.5 / 3)x3 + x4 　 = 5 　 (8)
    　　 (5 / 3)x2 - (1 / 3)x3 　 + x5 = 5 　 (9)
    式 (6) より，x2 を増加させれば，目的関数の値も増加することが分かります．つまり，現在の解は，最適解でないことになります．

  6. 前回と同様にして，x2 の増加量を α とし，式 (7)～(9) より，変数 x1，x4，及び，x5 に対する条件式を導くと，以下のようになります． 
    x1 = (9 - α) / 3 ≧ 0
x4 = 5 - (3.5 / 3)α ≧ 0
x5 = 5 - (5 / 3)α ≧ 0
    これらの条件を満足する α の値は 3 になります．また，この解（x1 = 2, x2 = 3, x3 = 0, x4 = 1.5, x5 = 0）に対する，目的関数の値 z は 12 となります．（図の交点：③）

  7. 再び，現在の解が最適解か否かを調べます．変数 x3 と x5 の値が 0 ですので，x3，または，x5 を増加させることによって，目的関数の値が増加するか否かを調べます．そのためには，目的関数を，x3 と x5 を使用して書き直す必要があります．そこで，α = 3 を導出した式 (9) を使用し，他の式から x2 を削除します．
    最大： z = 12 - (4 / 5)x3 - (3 / 5)x5　(10)
    　　 3x1 + (6 / 5)x3 - 　 (3 / 5)x5 = 6 　 (11)
    　　 -(3 / 5)x3 + x4 - (3.5 / 5)x5 = 1.5 　 (12)
    　　 (5 / 3)x2 - (1 / 3)x3 + x5 = 5 　 (13)
    式 (10) より，x3，または，x5 を増加させることによって，目的関数の値を増加させることはできません．従って，得られた解が最適解となります．

　　以上見てきたように，単体法においては，すべての交点を調べることなく，制約条件を満足する交点だけを調べることによって解を見つけることが可能です．
１．３ 単体表の使用

　　1.2 節で説明した単体法の計算手順をまとめると以下のようになります．

  1. 何らかの方法で基底可能解を見つける（ 1.4 節参照）

  2. 得られた解が最適解であるか否かを調べる

  3. 最適解であれば終了し，そうでなければ，解を改良しⅱへ戻る

　　単体表を使用すると，単体法の計算手順をより機械的に行うことができます．この節では，1.2 節に示した例の解を，単体表を使用して求めてみます．その手順は，以下に示す通りです．

  1. スラック変数 x3，x4，及び，x5 を導入し，問題を以下のように書き換えます（目的関数の表現方法に注意してください）．
    3x1 + x2 + x3 　 　 = 9
    2.5x1 + 2x2 　 + x4 　 = 12.5
    x1 + 2x2 　 　 + x5 = 8
    z - 3x1 - 2x2 　 　 = 0
  2. 基底可能解（x1 = 0，x2 = 0，x3 = 9，x4 = 12.5，x5 = 8）を見つけ，以下に示すような表を作成します．基底変数に対応する行は，各方程式の係数が入ります．また，目的関数に対応する行は，目的関数を非基底変数だけで表現したときの係数が入りますが，現段階では既にそれが実現されていますので，上で示した目的関数の値とその係数がそのまま入ります．なお，基底可能解の欄の z には，現時点における目的関数の値が入ります．
    3. 基底変数 基底可能解 x1 x2 x3 x4 x5
    x3 9 3 1 1 0 0
    x4 12.5 2.5 2 0 1 0
    x5 8 1 2 0 0 1
    z 0 -3 -2 0 0 0
  3. 最適解か否かを調べます．表の一番下の行において，非基底変数の列（上の表の場合は，x1 と x2）にある数字の中に負の値のものがあれば，最適解でないことを示しています．上の表の場合，-3 と -2 ですので，最適解でないことになります．

  4. 負の値となっている非基底変数の内，絶対値の最大のもの（x1）を基底変数に入れます．その手続きは以下のようになります．

    1. 基底可能解の列の数値 9，12.5，8 を，x1 の列にある数値 3，2.5，1 で割った値が最小になるものを選びます．この要素をピボット要素（緑色の要素）と呼びます．ピボット要素は x3 の行にあるため，x3 が次の解における非基底変数となります．

    2. 基底変数 x3 を，新しい基底変数 x1 で置き換え，その行の各要素をピボット要素で割ります．

    3. 各行の x1 の係数が 0 になるように，基底変数 x1 の行を何倍かして各行に加算（または，減算）します．

    　　以上の結果，以下に示すような表が作成されます．

    基底変数 基底可能解 x1 x2 x3 x4 x5
    x1 3 1 1/3 1/3 0 0
    x4 5 0 3.5/3 -2.5/3 1 0
    x5 5 0 5/3 -1/3 0 1
    z 9 0 -1 1 0 0
  5. 負の値となっている非基底変数がありますので，ピボット変数を選択し（緑の部分），上記の手続きを繰り返します．その結果，以下に示すような表が作成されます．
    基底変数 基底可能解 x1 x2 x3 x4 x5
    x1 2 1 0 2/5 0 -1/5
    x4 1.5 0 0 -3/5 1 -3.5/5
    x2 3 0 1 -1/5 0 3/5
    z 12 0 0 4/5 0 3/5
  6. 表の一番下の行の非基底変数の列に，負の値になる要素がありませんので，得られた結果（x1 = 2, x2 = 3, x3 = 0, x4 = 1.5, x5 = 0）が最適解になり，目的関数の値は 12 となります．
１．４ 基底可能解の求め方

　　たとえば，
目的関数，

z = -x1 - x2

を，制約条件，

3x1 + 5x2 ≦ 15　　　(1)
-2x1 - x2 ≦ -5　　　(2)
x1 - x2 ＝ 1　　　(3)
x1， x2 ≧ 0

のもとで，最大にする．
という問題について考えてみます．まず，(2) 式の右辺が負ですので，両辺に -1 を乗じて以下のように変形します． 
2x1 + x2 ≧ 5   (2)
　　次に，前節と同様，スラック変数を加えて等式に変換します．ただし，(2) 式に対してはスラック変数を引くことになり，また，(3) 式は元々等式ですのでスラック変数を加えません．その結果，(1)式～(3)式は以下のようになります．
3x1 + 5x2 + x3 　 = 15
2x1 + x2 - 　 x4 = 5
x1 - x2 　 　 = 1
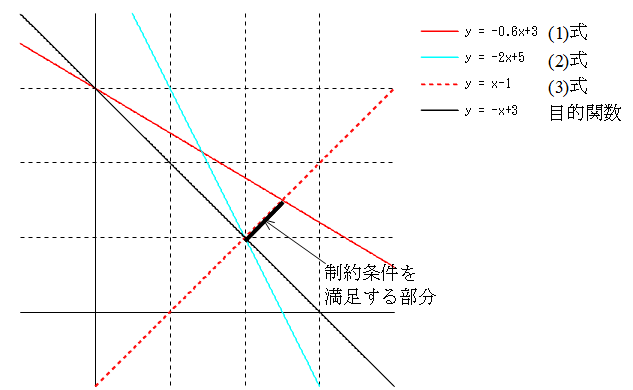
　　後は，前節と同様の方法で解けばよいわけですが，先の例のように，x1 = x2 = 0 は基底可能解になりません．一般的には，この例のように，基底可能解を簡単に見つけることができない場合が多くあります．実際，この問題を図を使用して解くと以下のようになり，目的関数の最大値は (2, 1) のとき，-3 になります．
　　そこで，基底可能解を求めるために，人為変数（人工変数） x5，x6 を導入し，制約条件式を，
3x1 + 5x2 + x3 　 　 　 = 15
2x1 + x2 - 　 x4 + x5 　 = 5
x1 - x2 　 　 　 + x6 = 1
のように変形するとともに，目的関数を， 
z = c1x1 + c2x2 + c3x3 + c4x4 + c5x5 + c6x6
	ただし，　c1 = c2 = c3 = c4 = 0,  c5 = c6 = -1
とします．この目的関数の値を 0 （目的関数の最大値，x5 = x6 = 0 で達成可能）とするような解があれば，その解は元の問題の基底可能解になります．そこで，変形された問題の最適解を求めることになりますが，その基底可能解は，直感的に求めることが可能です（この例では，x1 = x2 = x4 = 0 ）．したがって，単体表は以下のようになります．
基底変数 基底可能解 x1 x2 x3 x4 x5 x6
x3 15 = v3 3 = t11 5 = t12 1 = t13 0 = t14 0 = t15 0 = t16
x5 5 = v5 2 = t21 1 = t22 0 = t23 -1 = t24 1 = t25 0 = t26
x6 1 = v6 1 = t31 -1 = t32 0 = t33 0 = t34 0 = t35 1 = t36
z z0 z1 z2 z3 z4 z5 z6
なお，目的関数を非基底変数 x1，x2，x4 だけで表現する必要があります．具体的には，各 zi の値を， 
z0 = c3 * v3 + c5 * v5 + c6 * v6 = 0 * 15 - 1 * 5 - 1 * 1 = -6
zi = c3 * t1i + c5 * t2i + c6 * t3i    i = 1，2，4　　他は，0
のようにして計算し，その結果は以下のようになります（ z0 は，目的関数の値．z1，z2，z4 は，目的関数を x1，x2，x4 だけで表現したときの各変数に対する係数）．
基底変数 基底可能解 x1 x2 x3 x4 x5 x6
x3 15 3 5 1 0 0 0
x5 5 2 1 0 -1 1 0
x6 1 1 -1 0 0 0 1
z -6 -3 0 0 1 0 0
　　次は，一般の単体法を使用して，この最適化問題を解くことになります．そして，そこまでの段階をフェーズ１と呼びます．実際，解いてみると，以下のような結果が得られます．
基底変数 基底可能解 x1 x2 x3 x4 x5 x6
x3 4 0 0 1 2.666667 -2.666667 2.333333
x2 1 0 1 0 -0.333333 0.333333 -0.666667
x1 2 1 0 0 -0.333333 0.333333 0.333333
z 0 0 0 0 0 1 1
　　フェーズ１から基底可能解が求まりましたので，目的関数を元の関数， 
z = c1x1 + c2x2 + c3x3 + c4x4
	ただし，　c1 = -1, c2 = -1, c3 = c4 = 0
に戻し，単体法を継続します（フェーズ２）．ただし，その前に，目的関数が変更されましたので，単体表の一番下の行を先に述べた方法， 
z0 = c3 * v3 + c2 * v2 + c1 * v1 = 0 * 4 - 1 * 1 - 1 * 2 = -3
zi = c3 * t1i + c2 * t2i + c1 * t3i    i = 4　　他は，0
によって計算し直します．また，以後，人為変数の部分は必要ありませんので削除します．その結果，以下に示すような単体表が得られます．
基底変数 基底可能解 x1 x2 x3 x4
x3 4 0 0 1 2.666667
x2 1 0 1 0 -0.333333
x1 2 1 0 0 -0.333333
z -3 0 0 0 0.666667
　　一般的には，この状態から単体法を実行することになりますが，この例の場合，既に最適解が求まっています（非基底変数に対応する一番下の行に負の値がない）ので，フェーズ２は即座に終了します．

情報学部 菅沼ホーム SE目次 索引