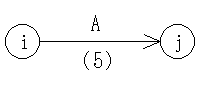スケジューリング

１．繰り返し型スケジューリング
２．プロジェクトスケジューリング（PERT/CPM）
1. ２．１プロジェクトスケジューリング
2. ２．２ PERTネットワーク

　　スケジューリング問題は，工場等での仕事のスケジュール，建設工事等のプロジェクトのスケジュール，バス・列車・航空機等のダイヤと乗員のスケジュール，要員（工場の作業者，病院の医師・看護婦等）のスケジュール，宅急便・郵便・ごみ等の集配スケジュール，大学・予備校等の時間割／教室割スケジュール等，様々な分野で発生します．

１．繰り返し型スケジューリング

　　工場（ショップ：shop）において，所要時間や納期遅れが最小になるように，各仕事（ジョブ：job）を各機械でどのような順序で加工すべきかを決めることは，非常に重要な問題です．仕事がすべて同じ機械順序で加工を受ける場合をフローショップ問題（ Flow Shop Problem ），また，仕事によって機械の処理順序が変化して良い場合をジョブショップ問題（ Job Shop Problem ）と呼びます．

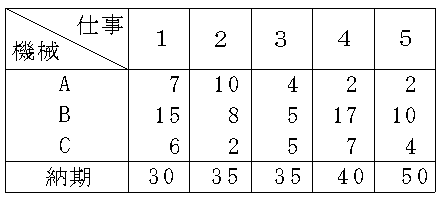
　　例えば，典型的なフローショップ問題として以下のような問題があります．5 つの仕事があり，各仕事に対する各機械での加工時間は，下の表に示すとおりです．仕事は，すべて，機械 A → B → C の順序で加工されるものとします．

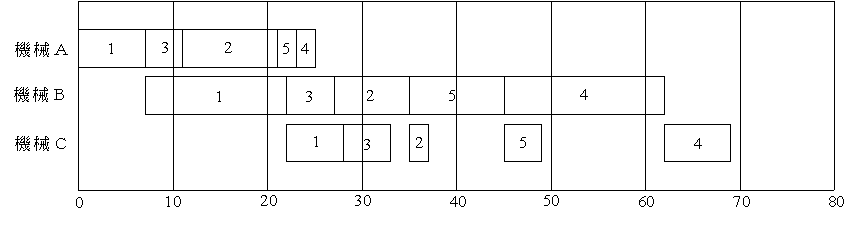
　　このとき，総所要時間や総納期遅れを最小にするように，例えば，以下に示すような加工順序を決めることになります（以下の図－ガントチャートと呼ぶ－は，あくまで例であり，最適解ではありません）．

　　残念ながら，フローショップ問題やジョブショップ問題に対する，一般的な解法は存在しません．特別な問題に対する解法，近似的な解法，または，組み合わせ最適化において述べた各手法を利用することになります．詳細については，省略します．

２．プロジェクトスケジューリング（PERT/CPM）

　　プロジェクトスケジューリングの手法には，PERT と CPM という 2 つの有名な方法があります．PERT は，1957～1958 年に，米国海軍，Booz, Allen and Hamilton 社，ロッキード社が共同でポラリスミサイルシステムの効率的開発のために考案したものであり，時間管理のみを考慮しています．また，CPM は，デュポン社とレミントン・ランド社が化学プラントの保全管理のため開発したものであり，費用の概念を強調しています．両者は，かなり似たものであるため，ここでは，PERT だけについて説明します．

２．１プロジェクトスケジューリング

　　PERT を使用したスケジュール管理は，一般に，以下のようにして行われます．

プロジェクト遂行のために必要な作業を列挙し，作業間の先行関係，各作業の実行に必要な時間や資源等を明らかにした上で，PERTネットワークを構築します．
PERTネットワークをもとに，各作業の開始時刻，完了時刻，余裕時間等を計算します．
PERT計算で得られたスケジュールが資源制約のもとで実行可能か否かを調べ，実行不可能であれば資源の要求が集中する部分の山崩し，資源の再投入等により実行可能な計画を得るための再スケジューリングを行います．

　　なお，以下における説明では，時間のみに注目し，資源や費用については考慮しないものとします．

２．２ PERT ネットワーク

　　簡単な例を元に，PERT ネットワークの作成・解析方法について説明します．

作業の所要時間及び先行関係： A～K の作業から成るプロジェクトがあり，各作業の所要時間（単位：日），及び，それらの先行関係は以下の通りであるとします．

作業	所要時間	先行作業	作業	所要時間	先行作業
A	5	-	G	4	D
B	3	-	H	3	D, E
C	2	-	I	5	H
D	2	A	J	1	G, I
E	8	B, C	K	2	H
F	5	C	L	2	F

PERT ネットワークの作成：上の表に基づき，PERT ネットワークを以下のルールに従って作成します．
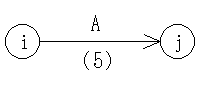
1. 各結合点には番号を与え，結合点 i から結合点 j にのびる矢印 ( i, j ) は作業を表し，i < j となるようにします．矢印上には，対応する作業，所要時間等を記入します．なお，ネットワーク全体には，プロジェクト開始と終了を示す結合点が一つずつなければなりません．
2. 結合点に入り込む作業がすべて終了したときに，当該結合点から出る作業を開始できます．
3. 二つの結合点の間には，高々一つの作業しか存在してはいけません．例えば，下図における左側の表記は許されません．ダミーの矢印を使用し，右図のように書かなければなりません．
4. 右図のように，結合点から出て，同一結合点に戻るループは存在してはいけません．
5. 矢印の長さと作業時間は無関係です．
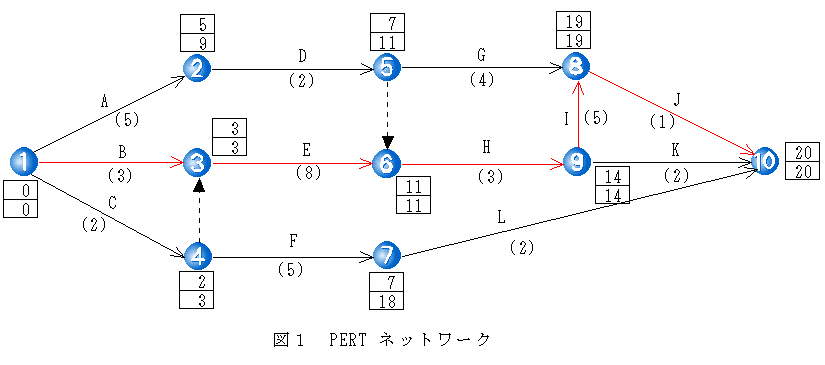
　　現在の例に対して PERT ネットワークを作成すると，以下のようになります．矢印上に書かれたアルファベットは作業，また，カッコ内の数字は作業時間です．なお，各結合点近傍に書かれた四角の中の数字については後ほど説明します．
最早開始時刻（ ES: Earlist Start Time ）の算出：時刻 0 にプロジェクトを開始したとき，ある結合点に最も早く到達可能な時刻，つまり，ある結合点に至るすべての作業が完了している最も早い時刻を計算します．この計算は，番号が小さな結合点から順に行われるため，前進計算と呼ばれます．今，

ES_j：結合点 j の最早開始時刻

p_ij：作業 (i,j) の所要時間

とすれば，以下のようにして計算できます．

ES_j = max_i {ES_i + p_ij}

　　具体的に計算した結果が，図1 における各四角内の上段の数字です．
最遅完了時刻（ LF: Latest Finish Time ）の算出：結合点 i の最遅完了時刻 LF_i とは，結合点 i を始点とする作業 p_ij によって結合されているすべての結合点 j へ，最早開始時刻前に到達するために，結合点 i に到達していなければならない時刻です．この計算は，プロジェクトの終了を表す結合点から順に行われるため，後退計算と呼ばれます．式で書けば，以下のようになります．

LF_i = min_j {LF_j - p_ij}

　　具体的に計算した結果が，図1 における各四角内の下段の数字です．この結果，最早開始時刻と最遅完了時刻が一致した結合点を結んだパスを．クリティカルパスと呼びます．クリティカルパスは，プロジェクトの総作業時間を決めるものであり，クリティカルパス上の作業の遅れは，全体の遅れに直接響くことになります．

余裕時間の算出：余裕時間とは，総作業時間に影響を及ぼさない範囲で，各作業に許される遅れ時間のことであり，以下のようなものが存在します．

作業 ( i, j ) の全余裕時間（ TF: Total Float ）： TF_ij = LF_j - (ES_i + p_ij)

　　先行する作業が遅れ無しに実行されたとき，プロジェクトの総所要時間に影響を与えない範囲で，作業 ( i, j ) が遅れても良い時間です．例えば，作業 L の全余裕時間は 11 になります．作業 L を開始するためには，作業 C と F を終了すれば可能です．つまり，7 日で開始可能です．しかし，結合点 10 へは，20 日までに到達すれば良いわけですから，作業 L の作業時間から，作業 L は，遅くとも 18 日に開始すれば問題ないことになります．つまり，(20 - 7 - 2) 日の余裕があるわけです．
作業 ( i, j ) の自由余裕時間（ FF: Free Float ）　FF_ij = ES_j - (ES_i + p_ij)

　　後続する作業に全く影響を及ぼさない範囲で，作業 ( i, j ) に許された遅れです．例えば，作業 G の自由余裕時間は 8 になります．明らかに，作業 G が，この範囲で遅れても，後続の作業 J の開始時刻には全く影響を及ぼしません．
作業 ( i, j ) の干渉余裕時間（ IF: Interfering Float ）　IF_ij = LF_j - ES_j

　　後続の作業に影響を及ぼす遅れです．例えば，作業 A の干渉余裕時間は 4 となります．明らかに，作業 A が遅れれば，作業 D の開始時間が影響を受けることになります．もちろん，この範囲内の遅れであり，他の作業が予定通り進めば，総作業時間には影響が出ません．

なお，各余裕時間の間には，以下のような関係があります．

TF_ij = FF_ij + IF_ij

図1 の例に対する各余裕時間は以下のようになります．

作業	ＴＦ	ＩＦ	作業	ＴＦ	ＦＦ
A	4	4	G	8	8
B	0	0	H	0	0
C	1	1	I	0	0
D	4	4	J	0	0
E	0	0	K	4	4
F	11	11	L	11	11

情報学部

菅沼ホーム

SE目次

索引