- 発注費,生産段取り費: K
- 商品の在庫管理の場合,発注量の多少に関わらずかかる費用を発注費といいます.例えば,通信費,書類作成費等がこれに当たります.また,製品の在庫管理の場合は,生産量の多少に関わりなくかかる費用に相当し,生産段取り費と呼びます.例えば,工作機械の再設定(部品の取り替え,ソフトの入れ替え等)に必要な時間・費用等がこれに当たります,
- 購入単価,生産費用: c
- 商品 1 単位を購入する費用(仕入れ価格,保険料,梱包費等)を購入単価,また,製品 1 単位を生産するために必要な価格(材料費,光熱費等)を生産費用と呼びます.
- 販売価格: p
- 商品または製品 1 単位を販売する価格です.
- 品切れ損失: s
- お客さんが来たとき,お客さんが買いたい商品が品切れであれば,せっかくの得られるべき利益を無駄にしてしまいます.この損失は,必ずしも,一時的なものに留まりません.店の信用を失い,二度と来店してくれないようなことになれば,将来的に大きな損失を生むことになります.
- 在庫保持費用: h
- 1 単位の商品・製品を,1 単位期間保管するために必要な費用です.この中には様々なものが含まれます.最も直接的なものは,倉庫の維持・管理費です.その他,保管することによる商品価値の低下もこの中に含まれます.また,在庫量に相当する金額を持っていれば,投資等によって利益が得られる可能性がありますが,在庫の状態では全く期待できません.このようにして失った利益もここに含まれます.
- 在庫保持費用を h (一定),時刻 t における在庫量を g(t) とすると,期間 [a, b] における総在庫保持費用は,以下のようにして計算できます.

- 確定需要,従属的
- 不確定需要,独立的
- 不確定需要,従属的
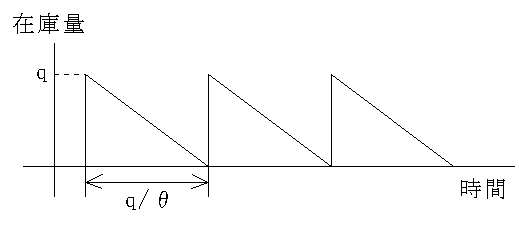
- 例1: 基本モデル
- 需要 = θ 単位 / 日
- 購入価格 = c / 単位 (購入個数に無関係)
- 発注費 = K (ただし,発注すれば即納入されるものとする)
- 在庫保持費用 = h / 単位・日
- 購入価格 = c / 単位 (購入個数に無関係)
製品在庫問題として考えれば,いかなる量の生産も瞬間的に可能であるという条件の下で,最適な 1 回の生産における生産量(生産ロットサイズ),及び,生産間隔を決めることになります.この最適な生産ロットサイズを,経済的ロットサイズ( ELS: Economic Lot Size )と呼びます.
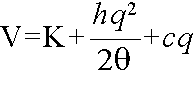
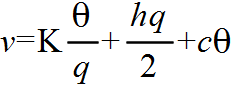

- 例2 : ロットサイズ決定問題
- 第 i 期の需要 = θi 単位 i = 1, 2, ・・・, n
- 第 i 期の製造単価 = ci / 単位
- 段取り費 = K (ただし,任意の量を一瞬に生産可能)
- 在庫保持費用 = h / 単位・期
- 第 1 期が始まる時点で在庫は 0 であり,また,第 n 期が終了した時点においても,在庫は 0 でなければならない.
- 品切れは許されない
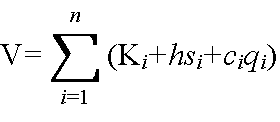
Vi(ai) = min [fi(qi) + Vi-1(ai - qi)] i = 2, ・・・, n 0 ≦ qi ≦ a a は総需要 V1(a1) = min [K1 + h s0 + c1 q1] = f1(a1) 0 ≦ q1 ≦ a
各期の需要(個): 40 35 50 20 30 35 各期の製造単価(万円/個): 10 10 10 10 10 10 段取り費(万円): 200 在庫保持費用(万円/個・期): 1
6 期: 総費用 2720 今期の生産量 0 今期の費用 35 5 期: 総費用 2685 今期の生産量 0 今期の費用 65 4 期: 総費用 2620 今期の生産量 0 今期の費用 85 3 期: 総費用 2535 今期の生産量 135 今期の費用 1550 2 期: 総費用 985 今期の生産量 0 今期の費用 35 1 期: 総費用 950 今期の生産量 75 今期の費用 950
6 期: 総費用 2300 今期の生産量 0 今期の費用 0 5 期: 総費用 2300 今期の生産量 0 今期の費用 0 4 期: 総費用 2300 今期の生産量 0 今期の費用 0 3 期: 総費用 2300 今期の生産量 0 今期の費用 0 2 期: 総費用 2300 今期の生産量 0 今期の費用 0 1 期: 総費用 2300 今期の生産量 210 今期の費用 2300
6 期: 総費用 3300 今期の生産量 35 今期の費用 550 5 期: 総費用 2750 今期の生産量 30 今期の費用 500 4 期: 総費用 2250 今期の生産量 20 今期の費用 400 3 期: 総費用 1850 今期の生産量 50 今期の費用 700 2 期: 総費用 1150 今期の生産量 35 今期の費用 550 1 期: 総費用 600 今期の生産量 40 今期の費用 600
- 仕入れ価格: c 円
- 販売価格: p 円
- 品切れ損失: s 円
- 売れ残り: d 円で処分,ただし,d < c < p
- 毎日の客数: y 人
- 販売価格: p 円
- 客数が y である確率(確率関数): f(y) y = 0, 1, 2, ・・・
- 客数が y 以下である確率(確率分布関数): F(y) = f(0) + f(1) + ・・・ + f(y)
- 平均客数: μ 人
v(x) = (期待収入) + (売れ残りに対する期待収入)- (仕入れ価格) - (期待品切れ損失)
= (客数がx人未満 + 客数がx人以上) + (売れ残りに対する期待収入)
- (仕入れ価格) - (期待品切れ損失)
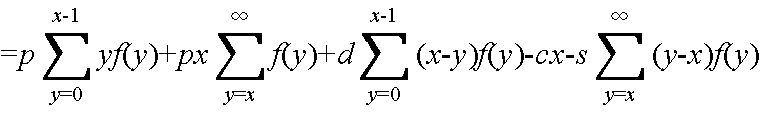
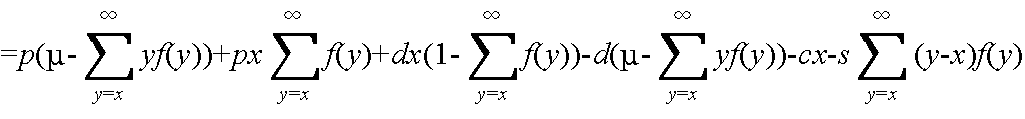
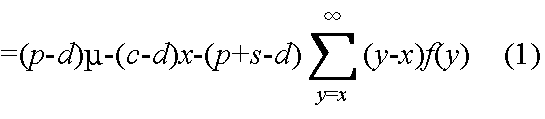
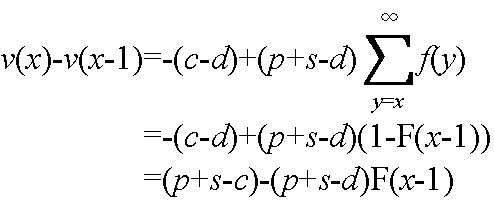
v(x) - v(x-1) >= 0,かつ,v(x+1) - v(x) <= 0
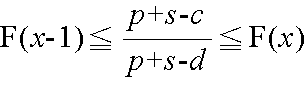
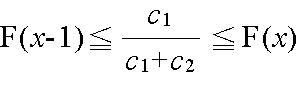
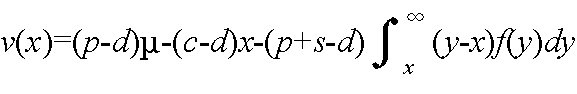
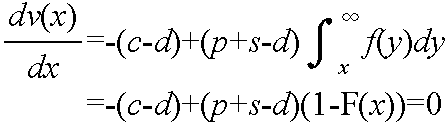
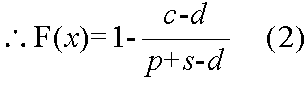
- 仕入れ価格: c = 30 円
- 販売価格: p = 70 円
- 品切れ損失: s = 0 円
- 売れ残り: d = 0 円で処分
- 毎日の客数: 平均 200,標準偏差 50 の正規分布 N(200, 502) で近似
- 販売価格: p = 70 円
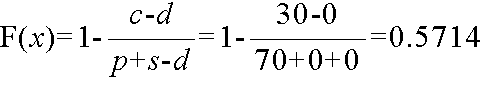
x = 50 * 0.1799 + 200 = 208.995
- 例3 : 実際的な問題
- 需要 = θ 単位 / 日 θ は,N(μ, σ2)
- 購入価格 = c / 単位 (購入個数に無関係)
- 発注費 = K
- 納入期間 = L 日間
- 在庫保持費用 = h / 単位・日
- 品切れの危険率 = δ
- 購入価格 = c / 単位 (購入個数に無関係)
- 定量発注方式(発注点方式)
- 納入期間 L を 0 とおき,かつ,需要として平均値を使用すると,経済的発注量は,以下のようになります.
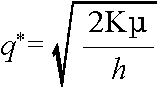
- 納入に L 日かかるため,L 日前に発注する必要があります.つまり,入荷した q* 単位の在庫が Lμ 単位に達っしたら,新たに q* 単位を発注することになります.
- 以上の計算では,需要の平均値を使用しているため,納入期間中に品切れが起きる確率は 0.5 になります.品切れの確率を 0.5 より小さく(この例では,δ)するためには,余裕を持って,在庫が Lμ より多い時点,つまり,在庫が Lμ + X ( X : 安全在庫)となった時点で発注する必要があります.また,この X は,
- P( L 日間の需要 > Lμ+X ) < δ
- となるように決定する必要があります.
- L 日間における需要は,平均 = Lμ,分散 = Lσ2 の正規分布をします.したがって,標準正規分布の100α%点( α = δ )を p とすると,
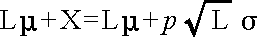
- となります.つまり,在庫が上記の値になったとき,q* 単位を発注することになります.
- JavaScript 版を使用すれば,任意の値に対して発注すべき時点に対する在庫量を画面上で計算できます.平均需要,発注費,在庫保持費用を画面上で変化させると(値を変えてその位置からフォーカスを外すと),経済的発注量も変化します.なお,結果は,小数点以下を四捨五入しています.
- 定期発注方式
- 発注間隔 T を決め,その時点における発注量 q を将来の需要予測に基づいて決めます.
- 納入期間 L < 発注間隔 T である場合
- t0 における発注量 q は,次の発注時点 t1(= t0 + T)における発注品が納入される時点 t2(= t1 + L)までの需要を満たす必要があります.この期間の平均需要は,(L + T)μ となりますので,発注量 q は,以下のようになります.
- q = (L + T)μ - (発注時点 t0 における在庫量)
- 納入期間 L > 発注間隔 T である場合
- 上とほぼ同様の検討から,発注量 q は,以下のようになります.
- q = (L + T)μ - (t0 における在庫量) - (t0 以前に発注したもので期間中に入荷する量)
- 上とほぼ同様の検討から,発注量 q は,以下のようになります.
- 安全在庫を見込む場合は,標準正規分布の100α%点を p とすると,上で計算した量に,
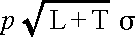
- を加えたものが実際の発注量になります.
- JavaScript 版を使用すれば,任意の値に対して定期的に行う発注の量を画面上で計算できます.納入期間 L > 発注間隔 T となるように値を変化させると(値を変えてその位置からフォーカスを外すと),「発注時点以前に発注したもので次の発注時点までに入荷する量」に対する入力フィールドも表示されます.なお,結果は,小数点以下を四捨五入しています.
