プログラム例 －様々な例題－

　　以下に示すプログラム例は，C++ 言語 におけるプログラム例を Python に変換したものです．変換は，基本的に，以下に示すような方法で行いました．

1. コメント記号 /* や // を # に変更（複数行のコメントも考慮）

2. 文末のセミコロン ; を削除

3. Python の仕様にないインクリメント演算子，デクリメント演算子，条件演算子，switch 文などを修正

4. 入出力や配列は Python の仕様に合わせて修正（配列は NumPy を使用）

5. 条件文や繰り返し文の () や {} を削除後， : を追加し，for 文に対しては，range 型によって修正（かなり面倒）

6. クラスのメンバー変数に対して，self. を追加．見落とした場合，その行の実行時にしかエラーメッセージが出力されないため，見落としの確率が高い．

　　なお，字下げに関しては，C/C++ のプログラムにおいて適切な字下げを行っていれば，全く問題ありません．ただし，以下の例を変換する際に，C/C++ のプログラムにおいて 1 箇所だけ不適切な字下げを行っている箇所がありました．この字下げは，いずれの言語においてもエラーにならない箇所でしたが，Python のプログラムの実行結果に大きな影響を与える箇所でした（ C/C++ では，問題ありません）．このような誤りが最も危険かもしれません．なお，簡単な実行チェックは行いましたが，一部，エラーが残っている可能性もありますのでご注意ください．

　　基本的に，プログラムを記述したファイルを test.py とすれば，

py -3 test.py [入力データファイル名, ･･･]		

とコマンドプロンプト上で入力すれば実行可能です．あとは，入力促進メッセージに従ってデータを入力してください．入力データが多い場合は，必要なデータをファイルに記述しておき，入力に対するリダイレクトを行うことによっても可能です（入力促進メッセージが気になりますが）．なお，プログラムによっては，[ ] 内に示したように，入力データをファイルに記述しておき，そのファイル名を入力するような形で実行する場合もあります．

　　また，多くの場合，プログラムは 2 つのファイルから構成されています．一つは，メインプログラムに相当する test.py です（プログラム例の下の方に記述）．例外はありますが，一般的に使用可能な関数やクラスの定義はファイル function.py に記述し，それを test.py で import するようにしています．さらに，画面上でそのまま実行できるように，ほとんどの例に対して JavaScript による記述も示してあります．

1. 数値計算
   1. 連立線形方程式，逆行列（ガウス・ジョルダン）
   2. 非線形方程式（二分法）
   3. 非線形方程式（セカント法）
   4. 非線形方程式（ニュートン法）
   5. 代数方程式（ベアストウ）
   6. 行列の固有値（フレーム法＋ベアストウ法）
   7. 実対称行列の固有値・固有ベクトル（ヤコビ法）
   8. 最大固有値と固有ベクトル（べき乗法）
   9. 数値積分（台形則）
   10. 数値積分（シンプソン則）
   11. 微分方程式（ルンゲ・クッタ）
   12. 補間法（ラグランジュ）
   13. 補間法（スプライン）
   14. 補間法（ベジエ曲線）
2. 最適化
   1. 最適化（線形計画法）
   2. 最適化（黄金分割法）
   3. 最適化（多項式近似法）
   4. 最適化（最急降下法）
   5. 最適化（共役勾配法）
   6. 最適化（ Newton 法）
   7. 最適化（準 Newton 法）
   8. 最適化（シンプレックス法）
   9. 最適化（動的計画法）
   10. 分割法（ TSP ）
   11. 逐次改善法（ TSP ）
   12. 遺伝的アルゴリズム（ TSP，関数の最大値）
3. 確率と統計
   1. ガンマ関数
   2. 二項分布
   3. ポアソン分布
   4. 一様分布
   5. 指数分布
   6. 正規分布
   7. χ² 分布
   8. t 分布
   9. F 分布
4. 待ち行列
   1. 簡単な例
   2. 複雑な例
5. 多変量解析
   1. 最小二乗法
   2. 重回帰分析
   3. 正準相関分析
   4. 主成分分析
   5. 因子分析
   6. クラスター分析
   7. 分散分析
6. ニューラルネットワーク
   1. Hopfield ネットワーク
   2. パーセプトロン
   3. Winner-Take-All
   4. 競合学習
   5. バックプロパゲーション
7. その他
   1. ボード線図
   2. ファジイ推論
   3. ソートと探索

1. 数値計算

   1. 連立線形方程式，逆行列（ガウス・ジョルダン）（ C/C++ の場合）

      　　添付したプログラムは，連立線形方程式の解（逆行列）をガウスの消去法によって求めた例です． JavaScript 版では，任意のデータに対して，連立方程式の解，逆行列，行列の乗算，及び，行列式の値を画面上で計算することが可能になっています．

   2. 非線形方程式（二分法）（ C/C++ の場合）

      　　添付したプログラムは，f(x) = exp(x) - 3x = 0 の根を二分法で求めた例です．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で解を求めたい式を入力することによって，任意の非線形方程式の解を画面上で求めることができます．

   3. 非線形方程式（セカント法）（ C/C++ の場合）

      　　添付したプログラムは，f(x) = exp(x) - 3x = 0 の根をセカント法で求めた例です．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で解を求めたい式を入力することによって，任意の非線形方程式の解を画面上で求めることができます．

   4. 非線形方程式（ニュートン法）（ C/C++ の場合，多次元：C/C++ の場合）

      　　添付したプログラムは，f(x) = exp(x) - 3x = 0 の根をニュートン法で求めた例です．多次元の場合に対するプログラムは，3 点 ( 0.5, 1.0 )，( 0.0, 1.5 )，( 0.5, 2.0 ) を通る円の中心座標と半径を多次元のニュートン法で求めた例です．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版（多次元の場合に対する JavaScript 版）では，JavaScript の仕様に適合した形で解を求めたい式を入力することによって，任意の非線形方程式の解を画面上で求めることができます．

   5. 代数方程式（ベアストウ）（ C/C++ の場合）

      　　添付したプログラムは，実係数代数方程式 (x + 1)(x - 2)(x - 3)(x² + x + 1) = 0 の解を，ベアストウ法で解いた例です．JavaScript 版では，任意のデータに対して画面上で解を得ることができます．

   6. 行列の固有値（フレーム法＋ベアストウ法）（ C/C++ の場合）

      　　添付したプログラムは，行列の固有値をフレーム法とベアストウ法によって求めるためのものです．JavaScript 版では，任意のデータに対して画面上で解を得ることができます．

   7. 実対称行列の固有値・固有ベクトル（ヤコビ法）（ C/C++ の場合）

      　　添付したプログラムは，実対称行列の固有値及び固有ベクトルを，ヤコビ法で求めるためのものです．JavaScript 版では，任意のデータに対して画面上で解を得ることができます．

   8. 最大固有値と固有ベクトル（べき乗法）（ C/C++ の場合）

      　　添付したプログラムは，行列の固有値と固有ベクトルを，固有値の絶対値が最大のものから順に求めていく方法（べき乗法）です．JavaScript 版では，任意のデータに対して画面上で解を得ることができます．

   9. 数値積分（台形則）（ C/C++ の場合）

      　　添付したプログラムは，台形則により sin(x) を 0 から π／２ までの積分するプログラム例です．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で積分したい式を入力することによって，任意の関数の積分を画面上で求めることができます．

   10. 数値積分（シンプソン則）（ C/C++ の場合）

       　　添付したプログラムは，シンプソン則により sin(x) を 0 から π／２ までの積分するプログラム例です．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で積分したい式を入力することによって，任意の関数の積分を画面上で求めることができます．

   11. 微分方程式（ルンゲ・クッタ）（ C/C++ の場合）

       　　添付したプログラムは，以下の微分方程式をルンゲ・クッタ法によって，0 から 1 秒まで解いた例です．JavaScript 版では，JavaScript の仕様に適合した形で微分方程式を入力することによって，任意の微分方程式の解を画面上で求めることができます．

       　　d²y/dt² + 3dy/dt + 2y = 1　　初期条件はすべて０

       　　（x[0] = y, x[1] = dy/dt)

   12. 補間法（ラグランジュ）（ C/C++ の場合）

       　　添付したプログラムは，ラグランジュ補間法のプログラムです．JavaScript 版では，n 次補間多項式による計算結果を画面上で求めることができます．

   13. 補間法（スプライン）（ C/C++ の場合）

       　　添付したプログラムは，3 次スプライン関数によってスプライン補間するためのものです．JavaScript 版では，任意のデータに対して，スプライン補間法による計算結果を画面上で求めることができます．

   14. 補間法（ベジエ曲線）（ C/C++ の場合）

       　　添付したプログラムは，ベジエ多角形を B₀ = (1 1)，B₁ = (2 3)，B₂ = (4 3)，B₃ = (3 1) としたとき，対応するベジエ曲線を描くためのものです．JavaScript 版では，任意のデータに対して，ベジエ曲線上の座標を画面上に出力することができます．

2. 最適化

   1. 最適化（線形計画法）（ C/C++ の場合）

      　　添付したプログラムは，線形計画法に対するプログラム例です．実行に関しては，使用方法を参考にしてください．JavaScript 版では，画面上で実行することができます．

   2. 最適化（黄金分割法）（ C/C++ の場合）

      　　添付したプログラムは，f(x) = x⁴ + 3x³ + 2x² + 1 の最小値を黄金分割法で求めた例です．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．

   3. 最適化（多項式近似法）（ C/C++ の場合）

      　　添付したプログラムは，f(x) = x⁴ + 3x³ + 2x² + 1 の最小値を多項式近似法で求めた例です．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．

   4. 最適化（最急降下法）（ C/C++ の場合）

      　　添付したプログラムは，最急降下法を使用して，非線形関数の最小値を求めるためのものです（プログラムの使用方法）．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい式を入力することによって，任意の関数の最小値を画面上で求めることができます．

   5. 最適化（共役勾配法）（ C/C++ の場合）

      　　添付したプログラムは，共役勾配法を使用して，非線形関数の最小値を求めるためのものです（プログラムの使用方法）．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい関数を入力することによって，任意の関数の最小値を画面上で求めることができます．

   6. 最適化（ Newton 法）（ C/C++ の場合）

      　　添付したプログラムは，Newton 法を使用して，非線形関数の最小値を求めるためのものです（ プログラムの使用方法）．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい関数を入力することによって，任意の関数の最小値を画面上で求めることができます．

   7. 最適化（準 Newton 法）（ C/C++ の場合）

      　　添付したプログラムは，準 Newton 法を使用して，非線形関数の最小値を求めるためのものです（ プログラムの使用方法）．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい関数を入力することによって，任意の関数の最小値を画面上で求めることができます．

   8. 最適化（シンプレックス法）（ C/C++ の場合）

      　　添付したプログラムは，シンプレックス法を使用して，非線形関数の最小値を求めるためのものです（ プログラムの使用方法）．C/C++ と同様，関数名（関数のアドレス）を引数として渡すことが可能ですので，任意の関数に対して対応可能です．JavaScript 版では，JavaScript の仕様に適合した形で最小値を求めたい関数を入力することによって，任意の関数の最小値を画面上で求めることができます．

   9. 最適化（動的計画法）（ C/C++ の場合）

      　　添付したプログラムは，動的計画法を使用して，資源配分問題，0-1 ナップザック問題，及び，グラフ上の最短経路問題を解くためのものです．JavaScript 版では，画面上で実行することが可能です．

   10. 分割法（ TSP ）（ C/C++ の場合）

       　　添付したプログラム（使用方法）は，巡回セールスマン問題（ TSP ）を分割法によって解くためのものです．

   11. 逐次改善法（ TSP ）（ C/C++ の場合）

       　　添付したプログラム（使用方法）は，巡回セールスマン問題（ TSP ）を逐次改善法によって解くためのものです．

   12. 遺伝的アルゴリズム（ TSP，関数の最大値）　-> 使用方法

       [巡回セールスマン問題（ TSP ）]　（ C/C++ の場合）

       　　添付したプログラムは，巡回セールスマン問題（ TSP ）を遺伝的アルゴリズムによって解くためのものです．

       [関数の最大値]　（ C/C++ の場合）

       　　遺伝的アルゴリズムの基本事項を定義したクラス Species は，巡回セールスマン問題だけに適用できるわけではありません．後一つの例として，関数，

       f(x) = sin(3*x) + 0.5 * sin(9*x) + sin(15*x+50)
       の [0, 1] 区間における最大値を求めるためのプログラムを添付しておきます．

3. 確率と統計

   1. ガンマ関数（ C/C++ の場合）

      　　添付したプログラムは，ガンマ関数の値を計算するプログラムです．JavaScript 版では，任意のデータに対するガンマ関数の値を画面上で求めることができます．

   2. 二項分布（ C/C++ の場合）

      　　添付したプログラムは，グラフ出力を指定すると，ベルヌーイ試行を n 回行い，0 ～ n 回成功する場合に対する二項分布の密度関数および分布関数の値をファイルに出力します．また，グラフ出力を指定しないと，指定された値における密度関数および分布関数の値を出力します．JavaScript 版では，同様の処理を画面上で実行することが可能であり，結果はテキストエリアに出力されると共に，「確率（複数点）」を選択すればグラフも表示されます．

   3. ポアソン分布（ C/C++ の場合）

      　　添付したプログラムは，グラフ出力を指定するとポアソン分布の密度関数および分布関数の値を指定した範囲だけファイルに出力します．また，グラフ出力を指定しないと，指定された値における密度関数および分布関数の値を出力します．JavaScript 版では，同様の処理を画面上で実行することが可能であり，結果はテキストエリアに出力されると共に，「確率（複数点）」を選択すればグラフも表示されます．

   4. 一様分布（ C/C++ の場合）

      　　添付したプログラムは，グラフ出力を指定すると一様分布の密度関数および分布関数の値を指定した範囲だけファイルに出力します．また，グラフ出力を指定しないと，指定された値における密度関数および分布関数の値，または，％値を出力します．JavaScript 版では，同様の処理を画面上で実行することが可能であり，結果はテキストエリアに出力されると共に，「確率（複数点）」を選択すればグラフも表示されます．

   5. 指数分布（ C/C++ の場合）

      　　添付したプログラムは，グラフ出力を指定すると指数分布の密度関数および分布関数の値を指定した範囲だけファイルに出力します．また，グラフ出力を指定しないと，指定された値における密度関数および分布関数の値，または，％値を出力します．JavaScript 版では，同様の処理を画面上で実行することが可能であり，結果はテキストエリアに出力されると共に，「確率（複数点）」を選択すればグラフも表示されます．

   6. 正規分布（ C/C++ の場合）

      　　添付したプログラムは，グラフ出力を指定すると正規分布の密度関数および分布関数の値を指定した範囲だけファイルに出力します．また，グラフ出力を指定しないと，指定された値における密度関数および分布関数の値，または，％値を出力します．JavaScript 版では，同様の処理を画面上で実行することが可能であり，結果はテキストエリアに出力されると共に，「確率（複数点）」を選択すればグラフも表示されます．

   7. χ² 分布（ C/C++ の場合）

      　　添付したプログラムは，グラフ出力を指定すると χ² 分布の密度関数および分布関数の値を指定した範囲だけファイルに出力します．また，グラフ出力を指定しないと，指定された値における密度関数および分布関数の値，または，％値を出力します．JavaScript 版では，同様の処理を画面上で実行することが可能であり，結果はテキストエリアに出力されると共に，「確率（複数点）」を選択すればグラフも表示されます．

   8. t 分布（ C/C++ の場合）

      　　添付したプログラムは，グラフ出力を指定すると ｔ 分布の密度関数および分布関数の値を指定した範囲だけファイルに出力します．また，グラフ出力を指定しないと，指定された値における密度関数および分布関数の値，または，％値を出力します．JavaScript 版では，同様の処理を画面上で実行することが可能であり，結果はテキストエリアに出力されると共に，「確率（複数点）」を選択すればグラフも表示されます．

   9. F 分布（ C/C++ の場合）

      　　添付したプログラムは，グラフ出力を指定すると Ｆ 分布の密度関数および分布関数の値を指定した範囲だけファイルに出力します．また，グラフ出力を指定しないと，指定された値における密度関数および分布関数の値，または，％値を出力します．JavaScript 版では，同様の処理を画面上で実行することが可能であり，結果はテキストエリアに出力されると共に，「確率（複数点）」を選択すればグラフも表示されます．

4. 待ち行列

   1. 簡単な例（ C/C++ の場合）

      　　添付したプログラムは，待ち行列が 1 つで，かつ，サービス窓口の数が s （任意）であるような非常に簡単な待ち行列モデル

      

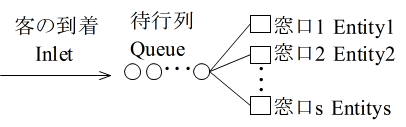
      をシミュレーションするためのものです．客の到着やサービスの分布は，すべて指数分布となっています（修正は，非常に簡単だと思います）．また，JavaScript 版では，画面上でシミュレーションを実行し，結果を得ることができます．なお，実行結果のカッコ内の値は，対応する項目に対する理論値です．

   2. 複雑な例（ C/C++ の場合）

      　　添付したプログラムは，先の例より複雑な待ち行列モデル

      

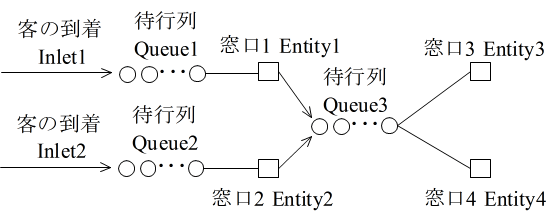
      をシミュレーションするためのものです．入力データによって，様々な構造のモデルに対するシミュレーションも可能です．また，到着時間に関しては，（指数分布，一定時間間隔，客の人数と到着時間の指定）の中から，また，サービス時間に関しては，（指数分布，一定時間）の中から選択可能です．プログラムの最後に，上の図に示したモデルをシミュレーションするための入力例，及び，最初に示した簡単な例に対する入力例が与えてあります．これらのデータをファイルに保存し，リダイレクトを行うことによっても実行可能です．

      　　JavaScript 版では，画面上でシミュレーションを実行し，結果を得ることができます．初期設定の状態は，上の図に示したモデルをシミュレーションするためのものです．入り口，待ち行列，窓口の数などを変えれば（変更して，その位置に対するフォーカスを外せば)，対応した状態が表示されます．なお，入り口，待ち行列，及び，窓口数の最大値は 10 に設定してありますが，ファイル complex.htm の 11 ～ 13 行目を修正することによって，容易に変更可能です．

5. 多変量解析

   1. 最小二乗法（ C/C++ の場合）

      　　添付したプログラムは，最小二乗法（多項式近似）を実行するためのものです．データの入力方法に関しては，プログラムの最後に提示してある入力例に対する説明を参考にして下さい．JavaScript 版では，任意のデータに対して画面上で実行することができます．

   2. 重回帰分析（ C/C++ の場合）

      　　添付したプログラムは，重回帰分析を行うためのものです．データの入力方法に関しては，プログラムの最後に提示してある入力例に対する説明を参考にして下さい．JavaScript 版では，任意のデータに対して画面上で実行することができます．

   3. 正準相関分析（ C/C++ の場合）

      　　添付したプログラムは，正準相関分析を行うためのものです．データの入力方法に関しては，プログラムの最後に提示してある入力例に対する説明を参考にして下さい．JavaScript 版では，任意のデータに対して画面上で実行することができます．

   4. 主成分分析（ C/C++ の場合）

      　　添付したプログラムは，主成分分析を行うためのものです．データの入力方法に関しては，プログラムの最後に提示してある入力例に対する説明を参考にして下さい．JavaScript 版では，任意のデータに対して画面上で実行することができます．

   5. 因子分析（ C/C++ の場合）

      　　添付したプログラムは，因子分析を行うためのものです．データの入力方法に関しては，プログラムの最後に提示してある入力例に対する説明を参考にして下さい．JavaScript 版では，任意のデータに対して画面上で実行することができます．

   6. クラスター分析（ C/C++ の場合）

      　　添付したプログラムは，クラスター分析を行うためのものです．データの入力方法に関しては，プログラムの最後に提示してある入力例に対する説明を参考にして下さい．JavaScript 版では，任意のデータに対して画面上で実行することができます．

   7. 分散分析（ C/C++ の場合）

      　　添付したプログラムは，分散分析を行うためのものです．データの入力方法に関しては，プログラムの最後に提示してある入力例に対する説明を参考にして下さい．JavaScript 版では，任意のデータに対して画面上で実行することができます．

6. ニューラルネットワーク

   1. Hopfield ネットワーク（ C/C++ の場合（連想記憶），C/C++ の場合（ TSP ））

      　　添付したプログラムは，Hopfield ネットワークを使用して，連想記憶を扱った例です．また，他の一つのプログラムは，Hopfield ネットワークを使用して，4 都市に対する巡回セールスマン問題（ TSP ）を扱った例です．JavaScript 版（連想記録，および，TSP）では，画面上で実行可能です．

   2. パーセプトロン（ C/C++ の場合）

      　　添付したプログラム（使用方法）は，p 個の入力ユニットと 1 個の出力ユニットからなるニューラルネットワークに対してパーセプトロン学習を行います．JavaScript 版では，画面上で実行可能です．

   3. Winner-Take-All（ C/C++ の場合）

      　　添付したプログラム（使用方法）は，p 個の入力ユニットと o 個の出力ユニットからなる Winner-Take-All ニューラルネットワークに対する学習を行います．Winner-Take-All ニューラルネットワークとは，出力ユニットの内，最大の出力を持つユニットだけが発火することによって，与えられたデータを分類しようとするものです．JavaScript 版では，画面上で実行可能です．

   4. 競合学習（ C/C++ の場合）

      　　添付したプログラム（使用方法）は，与えられた n 個のパターンを競合学習という教師無しの方法で分類するためのものです（入力ユニット数： p，出力ユニット数： o ）．JavaScript 版では，画面上で実行可能です．

   5. バックプロパゲーション（ C/C++ の場合）

      　　添付したプログラム（使用方法）は，任意の構造のネットワークをバックプロパゲーション法によって学習するためのものです．JavaScript 版では，画面上で実行可能です．

7. その他

   1. ボード線図（ C/C++ の場合）

      　　添付したプログラム（使用方法）は，伝達関数からボード線図を作成するのに必要なゲインと位相を計算するためのものです．計算された結果は，ゲインと位相が異なったファイルに

      周波数１  ゲイン１（または，位相１）
      周波数２  ゲイン２（または，位相２）　　　　　・・・・・・・				

      のような形式で出力されますので，gnuplot 等を使用すれば（「 set logscale x 」とし，x 軸を対数目盛にする必要がある）容易に図示することが可能です．なお，JavaScript 版では，グラフを表示し，グラフの色や線の太さを変更することが可能です．JavaScript 版では，式の数（グラフの数）や次数に制限をかけていますが（最大の式の数：5，最大次数：10 ），プログラム内の変数 max_g や max_order の値を変えることによって容易に変更できます．

   2. ファジイ推論（ C/C++ の場合）

      　　添付したプログラム（使用方法）は，以下に示すような m 個の変数を使用した n 個の規則を基にしてファジイ推論を行うものです．JavaScript 版では，画面上で実行することが可能です．テキストエリア内のデータの意味に関しては，使用方法を参照してください．

      if x₁ = A₁₁, x₂ = A₁₂, ･･･ ,x_m=A_1m then y = B₁

      if x₁ = A₂₁, x₂ = A₂₂, ･･･ ,x_m=A_2m then y = B₂

      　　　　　･････････････

      if x₁ = A_n1, x₂ = A_n2, ･･･ ,x_m=A_nm then y = B_n

   3. ソートと探索（ C/C++ の場合）

      　　プログラムでは，まず，リスト，及び，NumPy の配列に対し，ランダムに生成した 1,000,000 個のデータを記憶した後，ソートし，bisect_left，または，searchsorted によって探索しています．探索するデータは，最初に生成したデータの 10 個毎のデータです（ 100,000 個）．データを記憶するのにかかった時間，ソートにかかった時間，及び，探索にかかった時間を出力しています．

      　　次は，文字列の探索です．ランダムに生成した長さ 1,000,200 の文字列 data1（ bytearray ）に対して，5,000 個の長さ 200 の文字列を探索しています．5,000 個の文字列は，str の部分文字列であり，その内，半分には，文字列 data1 に含まれない文字が 1 文字含まれています．そのため，半分の文字列に対しては，探索しても見つからないことになります．データを記憶するのにかかった時間，及び，探索にかかった時間を出力しています．

      　　JavaScript 版では，表示された画面の「実行」ボタンをクリックすると，画面上で結果を見ることができます．なお，実行時間，データ数を多くするとブラウザが不安定になる，等の問題から，対象とするデータ数を減らしています．しかし，かなり時間がかかります．