- 2 進数
- 2 進数
- 我々は,通常,数値を表すのに 10 進数を使用する.10 進数では,0 から 9 までの 10 個の記号を使用し,各桁はその桁に対応した 10 のベキ乗の重みを持っている.例えば,365 や 3.14 は,以下のような意味を持っている.
- 365 = 3*102 + 6*101 + 5*100
- 3.14 = 3*100 + 1*10-1 + 4*10-2
- コンピュータでよく使用される 2 進数では,0 と 1 の記号だけを使用し,一般に,bnbn-1・・・b1b0.c1c2・・・cmと表現される.その意味するところは以下の通りである.
- bn*2n + bn-1*2n-1 + ・・・ + b1*21 + b0*20 + c1*2-1 + c2*2-2 + ・・・ + cm*2-m
- bi,cj: 0 または 1
- 例えば,10 進数の 6,17,0.25,3.625 は,2 進数では以下のように表現される.
- 6 = 4 + 2 = 1*22 + 1*21 + 0*20 = 110
- 17 = 16 + 1 = 1*24 + 0*23 + 0*22 + 0*21 + 1*20 = 10001
- 0.25 = 0*20 + 0*2-1 + 1*2-2 = 0.01
- 3.625 = 2 + 1 + 0.5 + 0.125 = 1*21 + 1*20 + 1*2-1 + 0*2-2 + 1*2-3 = 11.101
- 大きな数字を 2 進数で表現すると,桁数が非常に長くなる.この点を避けるため,8 進数や 16 進数もよく使用される.8 進数は 0 から 7 までの記号を,また,16 進数は 0 から 9 までに加えて A,B,C,D,E,および,F が使用される.各桁の重みが,それぞれ,8 のベキ乗,及び,16 のベキ乗である点を除いて,2 進数や 10 進数と考え方は同じである.
- なお,表現されている数字が何進数かを明確に表現するため,下の例のように,数字の右下に小さく何進数かを表す数字を書くことがある.
- (246)8 (101)10 (101)2
- 10 進数から 2 進数への変換
- 2 進数から 10 進数へ変換するには,その定義に従って,各桁の数字と対応した 2 のベキ乗をかけたものを加えていけば可能である.しかし,10 進数から 2 進数への変換は,多少面倒である.そこで,以下に述べるような方法がよく使われる.
- まず,整数に対しては,次の例のように,与えられた 10 進数を 2 で順に割っていき,各割り算における余りを求めるという方法が簡単である.
- 例:10 進数 26 を 2 進数へ変換
- 2)26
- 2)13 ・・・ 余り 0=a0
- 2) 6 ・・・ 余り 1=a1
- 2) 3 ・・・ 余り 0=a2
- 2) 1 ・・・ 余り 1=a3
- 0 ・・・ 余り 1=a4
- (26)10 = (a4a3a2a1a0)2 = (11010)2
- 小数点以下の数値に対しては,次の例のように,2 を順に乗じていき,その 1 の桁を 2 進数として採用していく方法がある.
- 例:10 進数 0.1 を 2 進数へ変換
- 0.1×2=0.2 ・・・ 0
- 0.2×2=0.4 ・・・ 0
- 0.4×2=0.8 ・・・ 0
- 0.8×2=1.6 ・・・ 1
- 0.6×2=1.2 ・・・ 1
- 0.2×2=0.4 ・・・ 0
- ・・・・・
- (0.1)10 = (0.000110・・・)2
- この例からも明らかなように,10 進数における小数点数を 2 進数に変換すると循環小数になってしまうような場合が起こる.この点は非常に重要である.データをコンピュータに記憶させる場合,必ず 2 進数に変換される.また,コンピュータに記憶できる桁数には制限がある.従って,循環小数になってしまうような場合,途中で打ち切らざるを得ない.つまり,上の例の場合,10 進数の 0.1 とコンピュータが内部に記憶している 0.1 に対応する数字は厳密には等しくないことになる.
- 2 進数に変換されれば,8 進数や 16 進数への変換は非常に簡単である.下の例のように,下位の桁から 3 ビットずつ,または,4 ビットずつ区切り,それぞれを,0 から 7,または,0 から F に書き換えてやれば,8 進数または 16 進数に変換できる.
- 例:(1111010111010011)2
- 8進数 1|111|010|111|010|011 → (172723)8
- 16進数 1111|0101|1101|0011 → (F5D3)16
- 2 進数
- 集合
- 集合とは
- ある定まった範囲にある対象をひとまとめにしたものを集合といい,集合を構成する一つ一つの対象を集合の要素,あるいは,元という.一般に,x が集合 A の要素であるとき,
- x ∈ A
- と表す.また,逆に,A の要素でないときは
- x ∈/ A
- と表す.
- 集合の例として,以下のようなものがあげられる.
- A = {x | x は整数で,かつ,0 < x < 6} 1 から 5 までの整数の集まり
- A = {1, 2, 3, 4, 5} 上と同じく,1 から 5 までの整数の集まり
- Z = {x | x は 1 以上の整数} 自然数の集合
- R = {x | x は実数} 実数の集合
- 集合にとって重要なのは,あるものが与えられたとき,それが集合の要素か否かを明確に判断できなくてはいけない点である.例えば,以下に示すものは,集合のように見えても集合ではない.
- E = {x | x は袋井に近い市町村}
- F = {x | x 小さい整数}
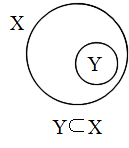
- 部分集合,全体集合,及び,空集合
- 集合 Y に含まれるすべての要素 y が,集合 X に含まれるならば,また,そのときに限って,集合 Y は,集合 X に含まれる(集合 Y は,集合 X の部分集合である)という.このことを形式的に記述すると,以下のようになり,図示すると右図のようになる(このような図を,ベン図と呼ぶ).
- Y ⊂ X ⇔ ∀y ∈ Y ならば y ∈ X
- ここで,記号「∀」は,「すべての」と読み,「∀y ∈ Y」によって,「集合 Y に含まれるすべての要素」を意味する.例えば,集合 X,Y,及び,Z を
- X = { 1, 2, 3 }, Y = { 1, 2, 3,4 }, Z = { 1, 2, 3, 5 }
- とすると,以下のようなことがいえる.
- X ⊂ Y ( X は Y の部分集合)
- X ⊂ Z ( X は Z の部分集合)
- 部分集合に対して,対象としているすべての要素を含む集合を全体集合という.また,一つも要素を含まない集合を空集合と呼び,φで表す.
- 和集合,共通集合(積集合),及び,補集合
- 2 つの集合 X,Y について,そのどちらかに含まれる要素からなる集合を X と Y の和集合といい,
- X ∪ Y (= {x | x ∈ X,または,x ∈ Y})
- と表す.X と Y の両方に含まれる要素からなる集合を X と Y の共通集合(積集合)といい,
- X ∩ Y (= {x | x ∈ X,かつ,x ∈ Y})
- と表す.
- また,全体集合を X としたとき,X の部分集合 E に対して,E に含まれない要素の集合を E の補集合といい,Ec で表す.形式的に,全体集合 X と空集合 φ について
- Xc = φ
- φc = X
- とする
- 上の定義で述べた関係をベン図で表すと,以下のようになる.
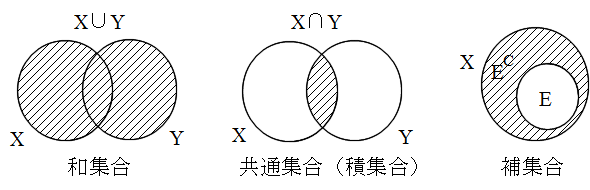
- 集合とは
- 論理演算
- 各変数が 0(偽)と 1(真)の値しかとらないとき,それらの変数や値間で行われる演算が論理演算である.論理演算には,OR(論理和.+,∨ なども使用される),AND(論理積.・,∧ なども使用される),及び,NOT(否定.~, ̄ なども使用される)という演算子が存在する.これらの演算子による演算結果は以下のようになる.
- X OR Y ( X + Y ): X または Y のいずれかが真の時,結果が真になる
- X AND Y ( X ・ Y ): X 及び Y の両者が真の時,結果が真になる
- NOT X ( ~X ): X が真の時に偽,X が偽の時に真になる
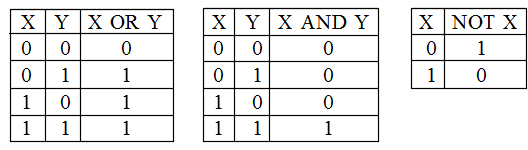
- また,各演算結果を真理値表を使って表現すれば,以下のようになる.なお,論理演算は,和集合の演算を論理和(∪ → OR),共通集合の演算を論理積(∩ → AND),及び,補集合の演算を否定(C → NOT)と見れば,先に述べた集合の演算と全く同じである.
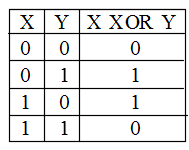
- その他,以下に示す排他的論理和( XOR,EOR)やド・モルガンの定理もよく使用される.
- 排他的論理和(右図): X XOR Y = ((NOT X) AND Y) OR (X AND (NOT Y))
- ド・モルガンの定理
- NOT (X AND Y) = (NOT X) OR (NOT Y)
- NOT (X OR Y) = (NOT X) AND (NOT Y)
- 順列・組合せ
- 順列
- いくつかのものの中から,順序を考えて並べたものを順列という.一般に,n 個の異なるものの中から,r 個の異なるものを取り出して作った順列の総数を nPr で表す.
- たとえば,A,B,C,および,D と書かれた 4 枚のカードから 3 枚を取り出したときの並べ方について考えてみる.まず先頭に来るカードの選び方として 4 通りある.2番目にくるカードの選び方は,先頭に来るカードをのぞいた中から選ぶので 3 通りとなる.先頭に選ばれた各カードに対して 3 通りあるので,結局,1番目と2番目のカードの並べ方は「 4 × 3 」通りあることになる.同様の議論を3番目のカードに対して行うことによって,結局,順列の総数は,
- 4 × 3 × 2 = 24 通り
- となる.一般に,
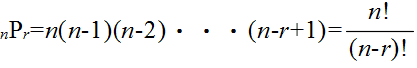
- となる.特に,r = n の場合は,以下のようになる.
- nPn = n (n - 1) (n - 2) ・・・3・2・1 = n !
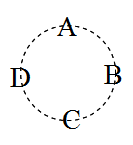
- 上に示すように,n 個の異なるものを1列に並べたときの順列の総数は n! になるが,円形に並べたときはどうであろう.円形に並べると,1列に並べたときとは異なり,どこが列の先頭かがはっきりしなくなる.たとえば,1列に並べた場合は,ABCD,BCDA,CDAB,DABC は異なる並び方であるが,円形に並べたときは右図に示すようにすべて同じ並べ方になる.このように,n 個の異なるものを円形に並べた場合,各並べ方毎に,どの位置を先頭とみなすかによって,n 種類の1列に並べる方法が対応している.つまり,1列に並べる方法は,円形に並べる方法の n 倍あることになる.一般に,n 個の異なるものを円形に並べたものを円順列といい,その総数は,
- n ! ÷ n = (n - 1) !
- 通りとなる.
- 次に,5 個の数字 1,2,3,4,及び,5 を使用して生成される 3 桁の整数の数について考えてみる.5 個の中から 3 個をとった並び方であるから 5P3 になりそうであるが,そうはならない.なぜなら,3 桁の整数には同じ数字が含まれていても構わないからである.まず,100 の位の選び方は 5 通りある.同じように,10 及び 1 の位に対しても 5 通りある.従って,全部で 5 × 5 × 5 通りあることになる.一般に,n 個の異なるものから,繰り返しを許して r 個とった順列を重複順列といい,その総数は,
- nr
- 通りとなる.
- [例1] A,B,C,D,E,F,および,G と書かれた 7 枚のカードを1列に並べたとき,A,B,C が一つのグループを形成するような並べ方( A,B,C がひとかたまりになっており,A,B,C の間に他のカードが入らない並べ方)は何通りあるか.
- A,B,C を併せて1枚のカードとみなしたときの並べ方: 5 ! = 120 通り
- A,B,C の並べ方: 3 ! = 6 通り
- ∴ 120 × 6 = 720 通り
- [例2] 5 個の数字 0,1,2,3,及び,4 を使用して,3 桁の整数を生成するとする.
- (1)3 桁の数字の個数は?
- 4 × 5 × 5 = 100 個(最初の数字は 0 ではいけない)
- (2)偶数の個数は?
- 4 × 5 × 3 = 60 個(最後の数字が 0,2,4 の場合)
- (3)5 の倍数の個数は?
- 4 × 5 × 1 = 20 個(最後の数字が 0 である場合だけ)
- 組合せ
- いくつかのものの中から,順序を考えずにその一部を取り出し一組にしたものを組合せという.一般に,n 個の異なるものの中から,r 個の異なるものを取り出して作った組合せの総数を nCr で表す.
- たとえば,A,B,C,および,D と書かれた 4 枚のカードから 3 枚を取り出す方法について考えてみる.まず1枚目のカードの選び方として 4 通りある.2枚目のカードの選び方は,1枚目のカードをのぞいた中から選ぶので 3 通りとなる.1枚目のカードの各選び方に対して 3 通りあるので,結局,1枚目と2枚目のカードの選び方は「 4 × 3 」通りあることになる.同様の議論を3枚目のカードに対して行うことによって,結局,選び方の総数は,
- 4 × 3 × 2 = 24 通り
- となる.
- しかし,これでは順列の総数と同じになってしまう.「1枚目に A,2枚目に B,3枚目に C」 を選んだ場合と,「1枚目に B,2枚目に C,3枚目に A」 を選んだ場合とでは,順列としては異なるが,順序を考えない組合せでは全く同じものとなる.要するに,組合せでは,何番目で選ばれたかを問題にする必要がないわけである.3枚のカードを選ぶ場合,順番の決め方としては 3 ! = 6 通りある.したがって,この例の場合,24 ÷ 6 = 4 通りが組合せの数になる.一般に,組合せの総数は,
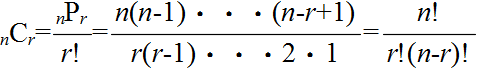
- となる.
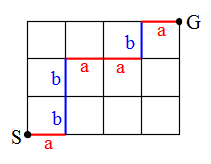
- [例3] 右図に示すような地図において,S 地点から G 地点まで最短距離でいく方法は何通りあるか.
- 右図には,一つの経路例が赤と青で示してある.水平方向への移動を a,垂直方向への移動を b で示せば,この経路は abbaaba と表せる.このように,最短経路では,必ず 7 本の道を通り,かつ,水平方向の道を 4 本(垂直方向の道を 3 本)通る.従って,7 本の道のうち,水平方向の道 4 本(垂直方向の道 3 本)の選び方が経路の総数になる.
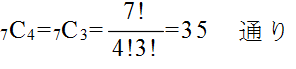
- 順列
- 確率と統計
- 事象
- 一定の条件の下で繰り返し行うことができ,その結果が偶然に支配されるような実験や観測を一般に試行という.また,試行によって起こる事柄を事象という.ある試行において,起こりうる結果全体の集合 X を全事象と呼び,すべての事象は X の部分集合で表される.特に,X の一つの要素だけからなる部分集合を根元事象,一つの要素も含まない事象(決して起こらない事象)を空事象といい,一般に φ で表す.
- [例1] 1 つのさいころを,1 回だけ投げることについて考えてみる.明らかに,この結果は偶然性に左右され,試行と考えることができる.このとき,全事象 X は,「k の目が出る」事象を k で表すと,
- X = {1, 2, 3, 4, 5, 6}
- となる.また,根元事象は,1, 2, 3, 4, 5, 及び, 6 となる.
- 事象 A または B が起こるという事象を A と B の和事象と呼び,和集合 A∪B で表す.また,事象 A と B が同時に起こるという事象を A と B の積事象と呼び,共通集合 A∩B で表す.たとえば,例1において,
- 事象 A : {1, 2, 3, 4} (4 以下の目が出る事象)
- 事象 B : (2, 4, 6} (偶数の目が出る事象)
- としたとき,その和事象と積事象は以下のようになる.
- A∪B : {1, 2, 3, 4, 6}
- A∩B : (2, 4}
- 全事象の中で,事象 A が起こらないという事象を A の余事象と呼び,
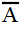
- と表す.たとえば,例1において,
- 事象 A : {1, 2, 3, 4} (4 以下の目が出る事象)
- としたとき,A の余事象は,{5, 6} となる.
- 事象 A と B が同時に起こることがない時,記号的には A∩B = φ である時,事象 A と B は互いに排反である,または,排反事象であるという.たとえば,例1において,
- 事象 A : {1, 3, 5} (奇数の目が出る事象)
- 事象 B : {2, 4, 6} (偶数の目が出る事象)
- としたとき,これらの事象は排反事象となる.
- 事象と確率
- 全事象 X に含まれるの各事象 A に対して次の 3 つの条件を満たす実数 P(A) が対応させられるとき,その値 P(A) を事象 A の起こる確率という.
- 任意の事象 A に対して,0 ≦ P(A) ≦ 1
- P(X) = 1, P(φ) = 0
- 事象 A と B が互いに排反,即ち A∩B = φ ならば,以下の関係が成立する.
- P(A∪B) = P(A) + P(B)
- ある試行において,全事象 X は,同じ程度に起こり易い n(X) = N 個の根元事象からなっているものとする.このとき,事象 A が n(A) = m 個の根元事象に分割されたとすると,事象 A の確率は以下のようになる.

- では,事象 A の余事象の確率はどのようになるのであろう.事象 A とその余事象は互いに排反であり,かつ,その間には,
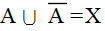
- のような関係がある.従って,確率の定義より,余事象の確率は以下のようになる.
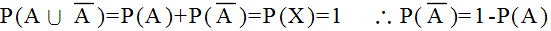
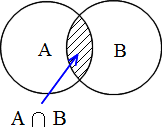
- 一般に,2つの事象が排反でない場合は,その和事象 A∪B の確率は,P(A) + P(B) とはならない.2つの事象 A と B が排反でないときは,右図に示すように,A∩B ≠ φ となるため,その和事象の確率は以下のようになる.
- P(A∪B) = A(A) + P(B) - P(A∩B)
- [例2] 1 つのさいころを,1 回だけ投げる試行において,今,
- 事象 A : {1, 2} (2 以下の目が出る事象)
- 事象 B : {3, 4, 5, 6} (3 以上の目が出る事象)
- とする.このとき,

- となる.また,事象 B は事象 A の余事象であるので,以下のようになる.
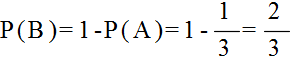
- [例3] 1 つのさいころを,1 回だけ投げる試行において,今,
- 事象 A : {2, 4, 6} (偶数の目が出る事象)
- 事象 B : {3, 6} (3 の倍数の目が出る事象)
- とする.明らかにこの2つの事象は排反ではない.従って,それらの和事象,
- A∪B : 偶数または 3 の倍数が出る事象
- の確率は,以下に示すように,A(A) + P(B) から「偶数で,かつ,3 の倍数である目が出る確率 P(A∩B)」を引いたものになる.
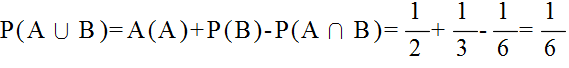
- 試行 T1 と T2 が,互いに各試行の結果に何らの影響を及ぼさないとき,試行 T1,T2は互いに独立であるという.2つの試行 T1,T2 が独立であるとき,試行 T1 で事象 A,試行 T2 で事象 B が起こる確率は,
- P(A)・P(B)
- となる.
- [例3] 1 つのさいころを,2 回投げたとする.明らかに,1回目の試行と1回目の試行は独立である.従って,いずれも偶数が出る確率は,1回目に偶数が出る確率 P(A) と2回目に偶数が出る確率 P(B) の積になり,
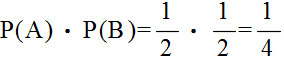
- となる.
- 平均値(集合平均,期待値),分散,及び,標準偏差
- 標本空間Ωで,ある属性について標本がとる可能性がある異なる数値が
- x1,x2,・・・,xk
- であるとする.各標本に対してそれのとる値を対応させる変数 X を考える.Ω上で X がそれぞれの値をとる確率が定まっているとき,X を確率変数といい,x1,x2,・・・,xk を X の標識という.確率変数 X が値 xi をとるという事象を
- { X = xi }
- で表し,その確率を
- P(X = xi) = pi (i = 1, 2, ・・・, k)
- で示す.
- 確率変数 X がある値 x に対して,X ≦ x である確率 P(X ≦ x ) を,確率変数 X の確率分布関数という.これを F(x) とすれば,次のようにかける.
- F(x) = P(X ≦ x)
- また,以下の関係を満たす関数 f(x) が存在するとき,それを確率密度関数という.
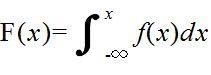
- ある確率分布の平均(集合平均,期待値),分散,及び,標準偏差は,以下のように定義される(σ2:分散,σ:標準偏差).
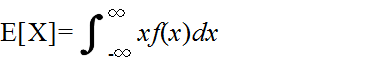
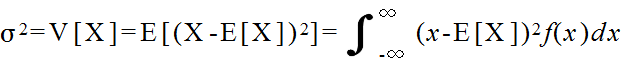
- 上の定義は,確率変数が連続的な値をとる場合であるが,サイコロを投げる場合のように離散的な値をとる場合は,積分でなく和として定義される.以下に,離散的な場合について説明する.
事象 A1 A2 ・・・・・ An 全事象 U 確率変数 X x1 x2 ・・・・・ xn - 確率 P(A1) P(A2) ・・・・・ P(An) 1.0 - 今,上に示す表において,事象 A1,A2,・・・,An が互いに排反であり,かつ,
- 全事象 Y = A1∪A2∪・・・∪An
- であるとする.また,各事象が起きるとき,確率変数 X が,x1,x2,・・・,xn という値をとるものとする.このとき,
- x1P(A1) + x2P(A2) + ・・・ + xnP(An)
- が平均となる.
- [例4] 下の表に示すようなくじ(くじの総本数は1000本)において,このくじを1本引いたときの賞金の平均は以下のようになる.
順位 1等 2等 3等 本数 1本 2本 5本 賞金 50000円 10000円 5000円 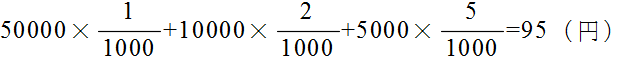
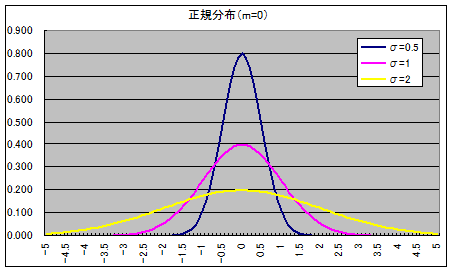
- 分散(標準偏差)は,データのばらつきを表す指標であり,大きいほど,ばらつきが大きいことを示す.例えば,確率密度関数が以下のようになる正規分布(平均:m,分散:σ2)は,非常によく使われる分布であるが,その分散による変化は右図のようになる.
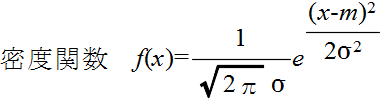
- 事象
- 情報量の単位
- コンピュータで扱うすべての情報(命令,データ)は,0 と 1 の 2 つの状態(をとる要素)の組み合わせによって記述される.0 と 1 の 2 つの値からなる要素の n 個の並び(ビット列)の長さを n ビット( bit )であるという.通常,8 ビットを基準とすることが多く,8 ビットを 1 バイト( byte )と呼ぶ.また,さらに長いビット列の長さを表現するため,
- 1024 バイト = 1キロバイト(KB) 注:1024 = 210
- 1024 キロバイト = 1メガバイト(MB)
- 1024 メガバイト = 1ギガバイト(GB)
- 1024 ギガバイト = 1テラバイト(TB)
- などの単位が使用される.
- 上に示したように,パソコン等においては,キロを 1024 として換算する場合が多いが,一般的には,キログラムやキロメートルという単位に使用されるように,キロは 1000 を表す.参考のため,一般的な単位の接頭辞を以下に示す.
接頭辞 発音 大きさ 接頭辞 発音 大きさ K キロ 103 m ミリ 10-3 M メガ 106 μ マイクロ 10-6 G ギガ 109 n ナノ 10-9 T テラ 1012 p ピコ 10-12 - ディジタル化
- 数値の表現方法
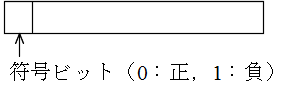
- まず,最初に,整数の表現方法について説明する.通常,整数は 2 バイト( 16 ビット),4 バイト( 32 ビット),8 バイト( 64 ビット)等で表現される.その表現方法は,先に述べた 2 進数の表現方法と基本的に同じである.ただし,右図に示すように最上位のビットは符号ビットとして使用される(符号ビットを使用しない表現方法も存在する)ので,n ビットを使用する場合,正の整数であれば,0 ~ 2n-1-1 (符号ビットを使用しない場合は,0 ~ 2n-1 )までの値を表現可能になる.例えば,32 ビットで整数を表現する場合,10 進数の 3 は,00000000000000000000000000000011 となり,表現可能な最大の正数は,231-1 = 2147483646 となる.なお,符号ビットを使用しない場合(常に,正の数),0 ~ 232-1 = 4294967294 の数値を表現可能となる.
- 負の整数の表現には注意する必要がある.通常,減算が加算により実行できることから,コンピュータでは 2 の補数表現がよく使用される.2 の補数は,2 進数の 0 と 1 とを反転し,最下位の桁に 1 を加えたものになる.従って,10 進数の -3 に対する内部表現は,10000000000000000000000000000011 とはならず,11111111111111111111111111111101 となる.

- 例えば,0.1245×10-23 のように,小数点を持つ数字,浮動小数点数 N(数学でいう,実数に対応)は,一般に,
- N = M × RE M:仮数, R:基数, E:指数
- の形で表現できる.コンピュータにおいても,通常,4 バイトまたは 8 バイトを使用して,右図のように表現される.符号ビットは,全体の符号を示し,0 なら正,1 なら負である.指数の符号は,指数部に含まれる.また,基数としては,2 や 16 が使用される.浮動小数で数を表した場合,仮数部のビット数でその数の有効桁数が決まるが,4 バイトを使用した場合,その有効桁数は 7 桁程度である.
- 文字の表現方法
- コンピュータ内部では,文字もビット列で表す.従って,どのようなビット列が何という文字に対応しているかの約束事が必要になる.このような約束事を文字コードと呼ぶ.欧米で使用されるのはアルファベット,数字,何種類かの記号だけであるので,8 ビット( 256 種類の文字を表現可能)で 1 文字を表せば十分であるが,日本語の場合,漢字があるため 2 バイトで 1 文字を表す文字コードを使用する必要がある.
- すべてのコンピュータで同じ文字コードを使用していれば問題ないが,後に示すように,様々な文字コードが存在する.従って,異なるコンピュータで同じプログラムやデータを使用したい場合は,場合によっては文字コードの変換が必要になる.また,改行を表す文字コードは,OS によって異なる.UNIX や MacOS では LF,旧 MacOS では CR,また,Windows では CR + LF が使用される.
- 文字コードが同じであっても,明朝体,ゴチック体など,その書体が異なれば,画面表示や印刷時における文字(の形)は異なってくる.この書体のことをフォントといい,フォントには,点(ドット)の集まりで文字を表現するビットマップフォント(ドットフォント)と,文字の輪郭を直線や曲線で表現するアウトラインフォント(ベクトルフォント)がある.ビットマップフォントは,拡大すると文字にぎざぎざが表れるので,アウトラインフォントが主流となっている.また,すべての文字の幅が等しい等幅フォントと,文字によって幅が異なる(例えば,W と i など)プロポーショナルフォントという分類も可能である.
- 音の表現方法
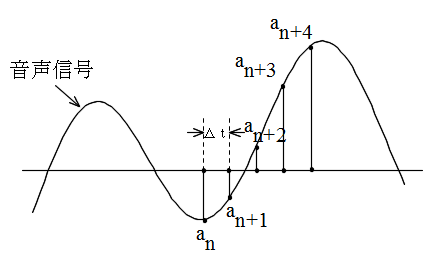
- 音声は,本来,空気の粗密波である.そのままでは,遠方へ伝達できないので右図のような電気信号に変換される.しかし,このような連続信号(アナログ信号)を直接コンピュータで扱うことはできない.そこで,音声信号の Δt 時間(サンプリング間隔)毎の値( an,an+1,an+2,・・・ )を取り出す,つまり,サンプリングすることになる.しかし,それらもアナログデータであるため,それをディジタルデータに変換する(ディジタル化,量子化)する必要がある.一般的には,その数値を 16 ビット( 2 バイト)の整数に変換(コード化)し,それらの値の時系列として音声を表現する.この方式を,PCM( Pulse Code Modulation )方式という.
- では,どのようなサンプリング間隔でデータを記録すればよいのであろうか.サンプリング定理によると,ある波形が含む最大周波数を f としたとき,1 / 2f 秒より短い間隔で記録すれば,記録されたデータから元の波形を復元できる.人間の最大可聴周波数は約 20 kHz であるので,サンプリング間隔を 1 / (2 * 20000) 秒以下にすればよいことになる.実際,CD のサンプリング周波数(サンプリング間隔の逆数)は 44.1 kHz になっている.電話で話すと相手の声が多少変わって聞こえるのは,電話の場合,サンプリング周波数が 8 kHz であるので,元のデータを完全には復元できないことが原因である.
- 40 kHz でサンプリングした場合,1秒間に 40000 個のデータを記録することになる.各データは 2 バイトで表されているので,1秒間に約 80 KB,1分間で約 4.8 MB のデータ,ステレオであるとこの 2 倍,約 9.6 MB のデータが必要になる.実際,音楽 CD は,PCM 方式を利用しており,サンプリング周波数 44.1 kHz で,各データを 16 ビットで表現している.このように,PCM 方式のままでは余りにもデータサイズが大きくなるため,圧縮して利用する場合も多くある.例えば,MP3 という圧縮形式では,CD の音質をほぼ維持したまま,1 / 10 程度のサイズまで圧縮可能である.
- 画像の表現方法
- 画像は,基本的に,点(画素,ピクセル)の集まりとして表現される.コンピュータ内では,1つの画素に関する情報を,R(赤),G(緑),及び,B(青)の各強さを各 8 ビットのデータに変換(ディジタル化,符号化)して保存している.つまり,1つの画素を表すためには,3 バイト必要になる.このような形式で保存された画像をビットマップ( BITMAP )形式と呼ぶ.
- ディスプレイの解像度を 1024 × 768 とすると,1画面を表すのに( 1024 × 768 × 3 )バイト = 2.25 MB 必要になる.動画になると,そのデータ量は更に増加する.動画は,1秒間に 15 ~ 30 枚の画像を連続して表示することによって作成される.1画像の大きさが 2.25 MB であり,1秒間に 30 枚の画像を表示するとすれば,1秒間に 67.5 MB,1分間に 4.05 GB のデータ量となる.このように,画像も大きなデータ量となるので,JPEG や GIF といった方法で,圧縮して使用する場合が多くなる.
- 数値の表現方法
- 代表的な文字コード
文字コード 特徴 ASCII コード ANSI(アメリカ規格協会)が制定した,7 ビット,または,パリティビットを加えた 8 ビットコード.パソコンなどで広く利用されている. EUC( Extended Unix Code,拡張 UNIX コード) UNIX( OS の一種) で使用されている 2 バイトコード JIS コード ANSI を基本にした 8 ビットコード JIS 漢字コード 文字コードの前後に全角文字であることを示すコードを挿入した 2 バイトコード シフト JIS コード 先頭バイトに全角か半角かの情報を持たせた 2 バイトコード Unicode 世界中の文字を表現できる 2 ~ 4 バイトコード.ISO で標準化されている. EBCDIC IBM が作成し,大型計算機で使用されている 8 ビットコード
- 配列
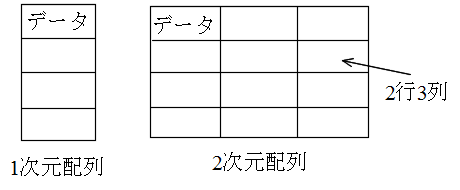
- 配列とは,データを直線状(1次元配列),表状(2次元配列)などに並べた構造である.各データを参照するには,データの位置を直接指定する.例えば,表状に並べたデータであれば,i 行 j 列のデータというように,データがある行と列を指定する.
- キューとスタック
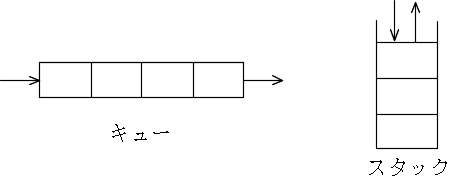
- キュー: 先に入れたデータを先に出す( FIFO:First in First out )形式のデータ構造である.待ち行列の表現などに使用される.
- スタック: 先に入れたデータを最後に出す( LIFO:Last in First out )形式のデータ構造である.スタックにデータを入れることを プッシュ( PUSH ),データを取り出すことを ポップ( POP ) という.プログラム内において,関数の処理順序を維持するためなどに使用される.
- キュー: 先に入れたデータを先に出す( FIFO:First in First out )形式のデータ構造である.待ち行列の表現などに使用される.
- リストと木構造
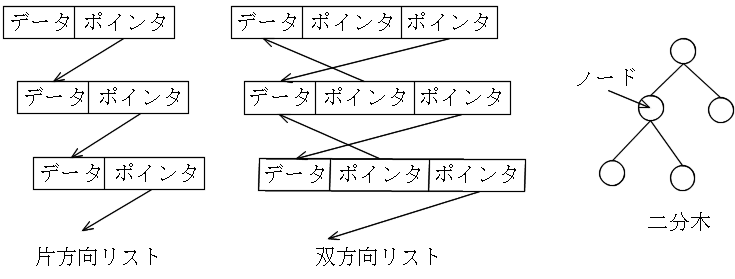
- リストとは,次のデータの位置をポインタを利用して示すデータ構造である.次のデータだけを指す片方向リスト,前のデータも示す双方向リストなどがある.また,木構造とは,データを木状に並べた構造であり,一つのノードから 2 本以内の枝が出ている木構造を,特に,二分木と呼ぶ.なお,木構造を表現するためには,リストが使用される場合が多い.
- ハッシュ法
- ハッシュ法とは,与えられたデータ内の数値やキー(以下,キーと呼ぶ)から,あらかじめ決められた手続き(ハッシュ関数)によって数値(ハッシュ値)を得,そのハッシュ値をデータの格納場所とする方法である.上で示したようなデータ構造の場合は,データの数が多くなれば,格納や検索に時間が掛かることになるが,ハッシュ法ではそのようなことはない.ただし,データの数が多くなると,異なるキーに対して同じハッシュ値が得られ,格納場所が同じになる現象(データの衝突)が発生する.そのため,それを避けるための手続きが必要となり,ある程度,検索や格納のための時間が増加する.なお,キーが同じであれば,必ず同じハッシュ値が得られる.また,ハッシュ値を,元のキーに戻すことはできない.
- 衝突を処理する代表的な方法としては,重複した場合に空いているハッシュ値にデータを振り分ける「オープンアドレス法」,同じハッシュ値を持つデータを線形リストとして保存する「直接連鎖法」などがある.
- ソート(並べ替え)
- バブルソート
- 隣り合う要素を比較して,大小の順が逆であれば,それらの要素を入れ替えるという操作を練り返す.具体的なアルゴリズムは以下のようになる.
- 配列 data[i] に n 個のデータが入っているものとする.
- i = 0, 1, ・・・, n-1
- i 番目のデータと i+1 番目のデータを比較し,もし,
- data[i+1] < data[i] (昇順の場合)
- であればそれらのデータを交換する.
- i = 0, 1, ・・・, n-2
- → この結果,data[n-1] に最も大きなデータが入ることになる
- 次に,最後のデータを除く n-1 個のデータに対し上の処理を繰り返す.
- 同様に,n-2,n-3,・・・個のデータに対して同じ処理を繰り返す
- 選択ソート
- (昇順の場合) まず配列を走査して,最も小さな要素を見つけだす.見つけたら,それを配列の先頭要素と交換する.この操作を配列の2番目の要素から始まるサブ配列について繰り返す.
- クイックソート:
- 中間的な基準値を決めて,それよりも大きな値を集めた区分と小さな値を集めた区分に要素を振り分ける.次に,それぞれの区分の中で同様な処理を繰り返す.例えば,次のようなデータが与えられたとする.このとき,左端のデータ( 37 )を枢軸要素と呼び,この要素がソート後の正しい位置にくるように以下の処理を行う(昇順の場合)
- 37 2 6 4 89 8 10 12 68 45
- 配列の右端の要素から順に枢軸要素 (37) と比較していき 37 より小さな要素があれば,その要素を 37 と交換する.
- 12 2 6 4 89 8 10 37 68 45
- 配列の左端(正確には,12 の直後の要素)から順に枢軸要素 (37)と比較していき,37 より大きな要素があれば,その要素を 37 と交換する.
- 12 2 6 4 37 8 10 89 68 45
- 配列の右端(正確には,89 の直前の要素)から順に枢軸要素(37)と比較していき,37 より小さな要素があれば,その要素を37と交換する.
- 12 2 6 4 10 8 37 89 68 45
- 以上の結果,37 の左には 37 より大きな要素はなく,また,その右側には 37 より小さな要素は無い状態となる.つまり,37 は,ソート後の正しい位置にあることがわかる.
- 37 の左側の配列(12 2 6 4 10 8),及び,右側の配列(89 68 45)に対して以上の処理を再帰的に繰り返す.
- バケツソート
- バケツソートとは,一次元配列に入っている n 個の正の整数をバケツ配列と呼ばれる 10×(n-1) の二次元配列を使用してソートする方法であり,以下に示すような手続きに従う.
- 一次元配列の各数値を一の位に基づいてバケツ配列の対応する各行に格納する.たとえば,一次元配列の中に数値 97,3,100 がこの順序で入っていたとすると,97 は行 7,3 は行 3,100 は行 0 に格納される.これを「分配パス」と呼ぶ.
- バケツ配列の各行に格納されている値を行 0 から順番に元の一次元配列の戻す.これを「収集パス」という.この時点で,一次元配列の中の値は 100,3,97 の順序になる.
- 以上の処理を数値の各位について繰り返す.
- シェルソート
- ある一定間隔おきに取り出した要素から成る部分列をそれぞれ整列し,更に間隔を詰めて同様の操作を行い,間隔が 1 になるまでこれを繰り返す.
- ヒープソート
- 未整列の部分を順序木に構成し,そこから最大値又は最小値を取り出して既整列の部分に移す.この操作を繰り返して,未整列部分を縮めていく.
- バブルソート
- 探索
- 線形探索法
- もっとも簡単な探索法であり,データの先頭から 1 つずつ比較を行い,一致するデータを探索する.一般に,探索速度は遅い.
- ハッシュ法
- 先に述べたように,与えられたデータ内の数値やキー(以下,キーと呼ぶ)から,あらかじめ決められた手続き(ハッシュ関数)によって数値(ハッシュ値)を得,そのハッシュ値をデータの格納場所とする方法であり,探索対象のデータのハッシュ値を計算すればそれがそのまま探索結果になり(衝突がない場合),高速な探索が可能である.ただし,データの大きさが小さければ,ハッシュ値に変換する手間が増えるためにかえって効率が悪くなることもある.
- 二分探索法
- 探索対象のデータはソートされているものとする(この説明では昇順とする).このとき,二分探索法のアルゴリズムは以下に示すとおりである.
- 探索すべきデータを探索先の中央のデータと比較する.
- そのデータより探索すべきデータの方が大きいときは後半のデータに対して,層でないときは,前半のデータに対して同じ処理を行う.
- 以下,一致するデータが見つかるまで,同様の処理を繰り返す.
- 線形探索法
- CORBA: OMG(オブジェクト指向技術の標準化,普及をすすめるために設立された業界団体)が定めた分散オブジェクト技術の仕様であり,異機種分散環境上のオブジェクト間でメッセージを交換するためのソフトウェアの仕様を定めている.
- プラグイン: アプリケーションソフトに機能を追加するための小さなプログラムであり,アプリケーション本体とは別に,個別に追加・削除などが可能である.
- コンパイラ言語
- アセンブラ言語: 機械語とほぼ 1 : 1 に対応した言語であるが,機械語とは異なり,命令などを 2 進数でなく記号で表現する.
- C: きめ細かい記述が可能であり,OS の記述など,利用範囲が広い汎用的な言語である.
- C++: C の発展系の言語であり,C にオブジェクト指向を付加した言語である.
- Java: C++ と似たオブジェクト指向言語であるが,C++ とは異なり,Window の生成などのグラフィカルな機能やネットワーク機能などを仕様に含んでいる.コンパイラによって中間言語(バイトコード)に翻訳してから,Java 仮想マシン( Java VM:Virtual Machine )上でインタプリタを介して実行される.特定の OS や CPU に依存せず,Java 仮想マシンさえ存在すれば,どのようなコンピュータ上においても実行可能である.そのため,Java アプリケーションとして単独でも実行可能であるが,Java アプレットという形でホームページに貼り付け,ブラウザによっても実行可能である.
- Java Beansは,Java で書かれたプログラムを,再利用可能なソフトウェアコンポーネントとして扱うための規約のことである.コンポーネントを組み合わせることによって,プログラミングの経験が少なくてもアプリケーションソフトを構築できる.
- Java サーブレット( Java Servlet )は,Web サーバ上で実行されるモジュール(部品)化された Java プログラムである.特定の OS やハードウェアに依存することがなく,あらゆる Web サーバで稼動させることができる.
- COBOL: 事務処理用に開発された汎用言語である.
- FORTRAN: 技術計算用に開発された汎用言語である.
- アセンブラ言語: 機械語とほぼ 1 : 1 に対応した言語であるが,機械語とは異なり,命令などを 2 進数でなく記号で表現する.
- インタプリータ言語
- JavaScript: 後に述べる HTML だけでは作成できない動的な Web ページを作成するための言語であり,クライアント側で動作する.
- PHP: JavaScript と同様,Web 作成用の言語であるが,サーバ側で動作するため,ファイル操作,データベース操作など,幅広い機能を持っている.
- Perl: PHP と同じような機能を持った言語である.一般に,PHP より高速で動作するが,プログラムが読みにくいという欠点がある.
- BASIC: 初期のパソコン用に開発された言語である.
- JavaScript: 後に述べる HTML だけでは作成できない動的な Web ページを作成するための言語であり,クライアント側で動作する.
- SGML( Standard Generalized Markup Language ): SGMLとは,他のマークアップ言語の基本となる言語であり,ISO8879 として標準化されている.文書の論理構造,レイアウト,装飾などをタグ付けによって記述することができる.各国の政府機関の公文書フォーマットとしても採用されている.
- HTML( Hyper Text Markup Language ): Web ページを記述するための最も標準的なマークアップ言語であり,SGML を Web ページ作成用に取り扱いしやすくした言語である
- XML( Extensible Markup Language ): HTML と同様,SGML から利用頻度の低い機能を取り除き,より扱いやすく手直しした言語である.インターネットを利用した企業間取引において,取引データをそのまま起票したり,社内文書に変換したりすることが容易にできる.また,HTML とは異なり,ユーザが独自のタグを指定できる.