- 探索の基本は線形探索，つまり，データの最初から一つずつ比較していく方法です．プログラム例は，データを配列（ new 演算子），又は，C++ 標準ライブラリ内の vector クラス（ Java の場合は ArrayList クラス）に順に保管した後，線形探索を行っています．このプログラムを実行すると以下のような出力が得られます．
配列と線形探索 保存： 50 ms 探索： 169219 ms データ数： 5000000 vectorと線形探索 保存： 101 ms 探索： 254485 ms データ数： 5000000
- プログラムからも明らかなように，データの数が前もって分かっているような場合は，配列を使用した方が有利です．vector は，データのサイズが分かっていないときは使用せざるを得ませんが，保存や探索するための時間がかかります（ ArrayList も同様）．いずれにしろ，線形探索には時間がかかります．
- 添付したプログラム例は，二分探索を行うためのものです．C の標準関数 bsearch，及び，C++ の標準ライブラリ内の binary_search を使用する方法も併記してあります（ Java に対しては，Arrays クラスの static メソッド binarySearch を使用）．二分探索を行うためには，配列内がソートされていなければなりません（ここ方法では，C++ の標準ライブラリ内の sort，また，Java に対しては，Arrays クラスの sort を利用）．
保存： 30 ms sort： 402 ms 探索： 40 ms 探索(bsearch)： 49 ms 探索(binary_search)： 39 ms
- 出力結果からも明らかなように，線形探索に比較して探索に要する時間は格段に早くなっています．ただし，ソートするための時間が加わり，保存時間が長くなっています．
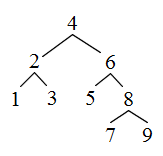
- 添付したプログラムは，二分探索木を使用して探索を行うためのものです．二分探索木とは，右図に示すように，各ノードにデータと 2 つのポインタを持ち，左のポインタでつながるデータはすべて自分より小さく，また，右のポインタでつながるデータはすべて自分より大きくなるような木です．このプログラムを実行すると以下に示すような結果が得られます．参考のため，一般に，二分木として実装されている C++ 標準ライブラリ内の set クラスを利用した場合も示しておきます．なお，Java の場合は，set に直接対応するものが存在しないため，TreeSet クラスを使用しています．
二分探索木 保存： 4742 ms 探索： 98 ms set 保存(set)： 4821 ms 探索(set)： 97 ms
- 配列を使用した場合に比較して，保存のための時間がかかっています（リスト構造を構成するためやむを得ない）．また，二分探索木は，入力されるデータの順番によって効率が大きく異なります．例えば，ソートされたデータを順番に追加していくと，線形探索と同じような探索時間がかかってしまいます．Java における TreeSet クラスは，二分探索木の一種である赤黒木を使用してこの問題を避けています．
- 添付したプログラムは，ハッシュ関数を使用して探索を行うためのものです．ハッシュ関数とは，データをある区間にできるだけ一様に分布する整数に変換する関数です．ハッシュ法においては，データをハッシュ関数を利用して整数に変換し，テーブル上のその整数で指定された位置に保存します．しかし，異なるデータが同じ位置を占める場合（データの衝突）があるため，それを回避する方法が必要です．このプログラムでは，衝突が起こった場合，それらのデータを上で説明した二分探索木を使用して保存しています．
- また，ハッシュを利用したコンテナである unordered_set クラスとの比較も行っています．このプログラムを実行すると以下に示すような結果が得られます．
Hash 保存： 8034 ms， 衝突回数： 1642507 探索： 35 ms unordered_set(string) 保存(string, unordered_set)： 9292 ms 探索(string, unordered_set)： 29 ms unordered_set(int) 保存(int, unordered_set)： 2256 ms 探索(int, unordered_set)： 7 ms
- ハッシュコードの生成や文字列への変換のため，二分探索木を使用した場合に比較して，保存のための時間がさらにかかっています．出力結果に見るように，unordered_set を利用した場合において，int 型データを使用した場合は，文字列に比較して，実行時間がかなり早くなっています．
- Java では，ハッシュ関数を自分で用意しなくても，String クラスの hashCode メソッド（様々なクラスに存在）を利用できます（プログラム）．さらに，HashSet クラスを利用すれば，より簡単にプログラム可能です（プログラム）．
- 横型探索と縦型探索
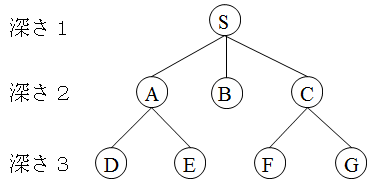
- ここでは，グラフの探索について考えてみます．最も基本的な探索方法は，横型探索（幅優先探索）と縦型探索（深さ優先探索）です．例えば，上図に示すようなグラフについて考えてみます．横型探索では，深さが浅いものから順に探索していきます．上図においては，S -> (A, B, C) -> (D, E, F, G) の順で探索していきます（括弧内の順序は任意）．最も簡単な方法は，キューを利用する方法です．キューの先頭要素（グラフのノード）を取り出し，それが目的とするノードでなければ，そのノードから到達できるノードをキューに追加する，といった操作を繰り返すだけです．プログラム例は，C++ 標準ライブラリ内の queue クラスを利用し，この方法で書かれています（ Java の場合は，ArrayDeque クラスを利用：
）．このプログラムを実行すると以下に示すような結果が得られます．なお，上記プログラム例には，再帰関数を使用したプログラム例も併記してあります．
S の追加 queue の状態： 先頭及び最後尾： S S， 要素数： 1 先頭 S を削除し，A, B, C を追加 queue の状態： 先頭及び最後尾： A C， 要素数： 3 先頭 A を削除し，D, E を追加 queue の状態： 先頭及び最後尾： B E， 要素数： 4 先頭 B を削除 queue の状態： 先頭及び最後尾： C E， 要素数： 3 先頭 C を削除し，F, G を追加 queue の状態： 先頭及び最後尾： D G， 要素数： 4 先頭 D を削除 queue の状態： 先頭及び最後尾： E G， 要素数： 3 先頭 E を削除 queue の状態： 先頭及び最後尾： F G， 要素数： 2 先頭 F を削除 queue の状態： 先頭及び最後尾： G G， 要素数： 1 先頭 G を削除 queue の状態： 空です
- 縦型探索では，深さが深いものから順に探索していきます．先の図においては，S -> C -> (F, G) -> B -> A -> (D, E) の順で探索していきます（括弧内の順序は任意）．S の次に，A または B を選択しても構いません．最も簡単な方法は，スタックを利用する方法です．スタックの先頭要素（グラフのノード）を取り出し，それが目的とするノードでなければ，そのノードから到達できるノードをスタックに追加する，といった操作を繰り返すだけです．横型探索と基本的な流れは同じですが，キューとは異なり，スタックでは最も最近追加したノードが先頭に来るため縦型探索になります．プログラム例は，C++ 標準ライブラリ内の stack クラスを利用し，この方法で書かれています（ Java の場合は，Stack クラスを利用：
）．このプログラムを実行すると以下に示すような結果が得られます．なお，上記プログラム例には，再帰関数を使用したプログラム例も併記してあります．
S の追加 stack の状態： 先頭： S， 要素数： 1 先頭 S を削除し，A, B, C を追加 stack の状態： 先頭： C， 要素数： 3 先頭 C を削除し，F, G を追加 stack の状態： 先頭： G， 要素数： 4 先頭 G を削除 stack の状態： 先頭： F， 要素数： 3 先頭 F を削除 stack の状態： 先頭： B， 要素数： 2 先頭 B を削除 stack の状態： 先頭： A， 要素数： 1 先頭 A を削除し，D, E を追加 stack の状態： 先頭： E， 要素数： 2 先頭 E を削除 stack の状態： 先頭： D， 要素数： 1 先頭 D を削除 stack の状態： 空です
- ここでは，グラフの探索について考えてみます．最も基本的な探索方法は，横型探索（幅優先探索）と縦型探索（深さ優先探索）です．例えば，上図に示すようなグラフについて考えてみます．横型探索では，深さが浅いものから順に探索していきます．上図においては，S -> (A, B, C) -> (D, E, F, G) の順で探索していきます（括弧内の順序は任意）．最も簡単な方法は，キューを利用する方法です．キューの先頭要素（グラフのノード）を取り出し，それが目的とするノードでなければ，そのノードから到達できるノードをキューに追加する，といった操作を繰り返すだけです．プログラム例は，C++ 標準ライブラリ内の queue クラスを利用し，この方法で書かれています（ Java の場合は，ArrayDeque クラスを利用：
- 最短経路問題
- 上で述べたように，閉路がないグラフ（木構造）に対する横型探索や縦型探索は非常に簡単です．しかし，上図のように閉路が存在するようなグラフの場合はそれほど簡単ではありません．なぜなら，一度チェックしたノードを再びチェックしないようにしないと無限ループに陥ってしまうからです．ここでは，上図におけるノード 0 から ノード 6 に至る最短経路を求めてみます（赤い線が最短経路，枝上の数値が経路の長さ）．
- プログラム例は，横型探索を使用してこの問題を解いています（
）．このプログラムでは，ノードの数だけの要素を持つ配列変数 rd に，スタートノードからの経路長を入れておく（まだ経路長が計算されていない場合は -1 ）ことによって，ループに入ることを防いでいます．また，縦型探索のプログラム例（）においても，同様の処理を行っています．これらのプログラムを実行すると以下に示すような結果が得られます．なお，上記プログラム例には，再帰関数を使用したプログラム例も併記してあります．
展開したノード数： 11， 最短距離： 16 // 横型探索の場合 展開したノード数： 8， 最短距離： 16 // 縦型探索の場合
- この例のように簡単な問題の場合は問題ありませんが，ネットワークが大きくなると単純な横型探索や縦型探索では余分なノードの生成を行い実行時間がかかってしまいます．より高速に解くためには，ノードの探索順序を何らかの知識に基づいて変更してやる必要があります．最短距離問題を解く方法として有名な Dijkstra 法（ダイクストラ法）は，ある意味で，知識に基づいた探索方法の一種であると言えます．
- Dijkstra 法では，まず，スタートノードから直接到達可能なノードまでの距離を計算します．それらのノードの内，最短距離でいけるノードは，他のノードを経由したいかなる経路によってもその距離より短い距離で到達することは不可能です．そこで，スタートノードからそのノードまでの距離は確定したとみなし，以後，検討対象から外します．次に，その最短距離のノードから直接到達可能なノードまでのスタートノードからの距離を計算します．このとき，あるノードまでの距離が，それまでに計算された距離（この場合は，スタートノードからの直接距離）よりも短ければ，そのノードまでの距離を新しい距離で置き換えます．再び，既に距離が計算されたノードの内，スタートノードからの距離が最小のものを選択し，同じ手続きを繰り返します（距離の確定とそのノードから直接到達可能なノードまでの距離の計算）．このようにして，すべてのノードまでの距離が確定した時点で終了となります．
- プログラム例（
）は，距離が最小になるノードが常に先頭に来る C++ 標準ライブラリ内の set クラスを利用して（ Java の場合は，TreeSet クラス） Dijkstra 法を実現しています．このプログラムを実行すると以下に示すような出力が得られます．ただし，この問題に対しては，set を使用しないで記述（上記のファイルの下部に併記してある）した方が簡単で，かつ，計算時間も短くなると思います．
展開したノード数： 7， 最短距離： 16
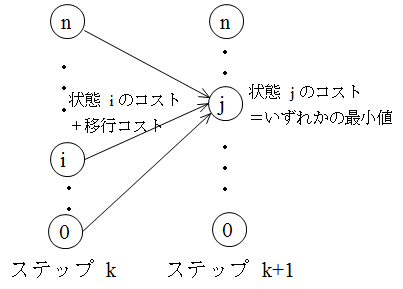
- あまり適切な例ではありませんが，この問題は動的計画法を使用しても解くことができます．動的計画法は，上図に示すように，ステップ (k+1) の状態 j におけるコストは，ステップ k の各状態におけるコストに，その状態からステップ (k+1) の状態 j に移行するためにかかるコストを加えたものの内最小（最大）のものになります．これを，初期状態から目標状態まで繰り返せば解が得られます．プログラム例（
）は，動的計画法によって最短距離問題を解いた例です．このプログラムを実行すると，以下に示すような結果が得られます．
ステップ： 6， 最短距離： 16
- 上で述べたように，閉路がないグラフ（木構造）に対する横型探索や縦型探索は非常に簡単です．しかし，上図のように閉路が存在するようなグラフの場合はそれほど簡単ではありません．なぜなら，一度チェックしたノードを再びチェックしないようにしないと無限ループに陥ってしまうからです．ここでは，上図におけるノード 0 から ノード 6 に至る最短経路を求めてみます（赤い線が最短経路，枝上の数値が経路の長さ）．
- ８パズル
- 次に，もう少し複雑な問題を解いてみます．８パズルでは，9 個のコマを置く場所が用意してあり，その中に 1 から 8 の 8 つのコマが置かれています．1 箇所だけコマが置かれていない場所がありますので，その上下左右にあるコマをそこに移動することが可能です．例えば，下の図に示すように，初期状態（各図の左側）から，できるだけ少ない回数のコマの移動によって，目標状態（各図の右側）に持って行くことになります．
- 例えば，上の左側の例では，以下に示すのが最適解になります．
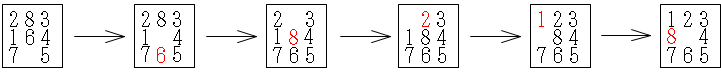
- プログラム例（
）は，横型探索によって上記の問題を解いた例です．同じ状態か否かをチェックするため C++ 標準ライブラリ内の map クラスを使用しています（ Java の場合は，TreeMap クラス）．以下に示すのが，このプログラムを実行した結果です．「展開とチェック」の後ろの数字の内，最初の数字が展開したノードの数（キューに入れられたノードの数），後ろの数字がそれらの内，解か否かをチェックしたノードの数です．右側の問題に対しては，かなり多くのノードを展開していることが分かると思います．なお，以下のプログラムにおいても同様ですが，このプログラムは最適解を得るためのものではありません．解が得られた時点でプログラムを終了しています．ただし，この問題の場合は，横型探索によって最適解が得られますので，得られた結果は最適解になっています．
例１ 展開とチェック： 62 35， 最短距離： 6 1 2 3 8 0 4 7 6 5 1 2 3 0 8 4 7 6 5 0 2 3 1 8 4 7 6 5 2 0 3 1 8 4 7 6 5 2 8 3 1 0 4 7 6 5 2 8 3 1 6 4 7 0 5 例２ 展開とチェック： 34299 22912， 最短距離： 19 1 2 3 8 0 4 7 6 5 1 2 3 8 4 0 7 6 5 1 2 0 8 4 3 7 6 5 1 0 2 8 4 3 7 6 5 1 4 2 8 0 3 7 6 5 1 4 2 8 6 3 7 0 5 1 4 2 8 6 3 7 5 0 1 4 2 8 6 0 7 5 3 1 4 2 8 0 6 7 5 3 1 4 2 0 8 6 7 5 3 0 4 2 1 8 6 7 5 3 4 0 2 1 8 6 7 5 3 4 2 0 1 8 6 7 5 3 4 2 6 1 8 0 7 5 3 4 2 6 1 0 8 7 5 3 4 2 6 0 1 8 7 5 3 0 2 6 4 1 8 7 5 3 2 0 6 4 1 8 7 5 3 2 1 6 4 0 8 7 5 3- プログラム例（
）は，縦型探索によって上記の問題を解いた例です．以下に示すのが，このプログラムを実行した結果です．縦型探索の場合は，深さ制限を入れないと，非常に時間がかかると共に最適解が得られる可能性が小さくなります．
例１ 展開とチェック： 61 60， 最短距離： 6 1 2 3 8 0 4 7 6 5 --- 省略 --- 2 8 3 1 6 4 7 0 5 例２ 展開とチェック： 11150 11139， 最短距離： 19 1 2 3 8 0 4 7 6 5 --- 省略 --- 2 1 6 4 0 8 7 5 3- この問題においても，どのノードを最初に展開すべきかを何らかの知識を使用して決めることにより，探索時間を短くすることが可能です．ここでは，各ノード（状態）に対して，以下に示す評価値を計算し，この値の小さいノードから順に探索していきます．
- f(n) = g(n) + h(n)
- g(n)： 節点 n の深さ
- h(n) = p(n) + 3s(n)
- p(n)： 各コマの正しい位置からの距離を加えた値
- s(n)： 中心以外のコマに対し，その次のコマが正しい順序になっていなければ 2，
- そうでなければ 0，中心の駒には 1 を与える事によって得られる得点
- プログラム例（
）は，この方法によって上記の問題を解いた例です．以下に示すのが，このプログラムを実行した結果です．なお，評価値が小さいものをキューの先頭に置くため，C++ 標準ライブラリ内の priority_queue クラスを使用しています（ Java の場合は，PriorityQueue クラス ）．
例１ 展開とチェック： 12 6， 最短距離： 6 1 2 3 8 0 4 7 6 5 --- 省略 --- 2 8 3 1 6 4 7 0 5 例２ 展開とチェック： 201 111， 最短距離： 19 1 2 3 8 0 4 7 6 5 --- 省略 --- 2 1 6 4 0 8 7 5 3 - 次に，もう少し複雑な問題を解いてみます．８パズルでは，9 個のコマを置く場所が用意してあり，その中に 1 から 8 の 8 つのコマが置かれています．1 箇所だけコマが置かれていない場所がありますので，その上下左右にあるコマをそこに移動することが可能です．例えば，下の図に示すように，初期状態（各図の左側）から，できるだけ少ない回数のコマの移動によって，目標状態（各図の右側）に持って行くことになります．
- プログラム例は，文字列の探索を，C/C++ の標準関数を使用した場合，1 文字ずつ単純に比較した場合（単純な方法），BM 法を使用した場合，及び，STL の string を使用した場合を比較しています．ただし，私が使用している g++ のバージョンにおいては，string ヘッダを include すると，strstr が正しく動作しなくなってしまいましたので，string を使用する場合は異なるプログラムとして記述しています．いずれの場合においても，約 1,000,000 個の文字からなるテキストから，200 個の文字からなる 5,000 個の異なるパターンを検索しています．なお，5,000 個のパターンの半数には，テキストに存在しない文字が含まれています．その出力結果は以下に示すとおりです．
***初期設定終了： 24 ms*** テキスト文字数 1000201 探索パターン数 5000 探索パターン文字数 200 標準関数 strstr 探索時間： 3062 ms 見つからなかったパターン数： 2500 単純な方法 探索時間： 231324 ms 見つからなかったパターン数： 2500 BM 法 探索時間： 1374 ms 見つからなかったパターン数： 2500 ----- STL の string を使用した場合 ----- ***初期設定終了： 59 ms*** テキスト文字数 1000201 探索パターン数 5000 探索パターン文字数 200 STL string の find 探索時間： 73412 ms
- ここで，BM 法とは以下に示すような方法です．例として，テキスト "xyzcdxxxkbxyccbbxcacbbxx" を対象として，パターン文字列 "cacbb" を探索する場合について説明します．
- パターンに現れる文字のずらし幅を決定します．つまり，パターンに現れる各文字に対して，その文字の右側に何文字存在するかの表を作成します．同じ文字が複数回現れる場合は，最も右側の文字だけを対象とします．この例の場合は，以下のようになります．
a b c 3 0 2 - 下に示すような位置において，パターンの右端の文字から対応するテキストの文字と比較していきます．
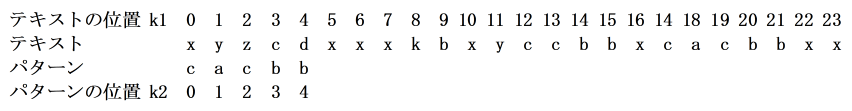
- 上の比較において，パターの右端の文字が異なっています．比較対象となるテキスト内の文字は 'd' ですが，この文字はパターンに含まれていません．そこで，以下に示すように 5 文字（パターンの文字列長）だけ右にずらします．
- 再びパターンの後ろから比較していくと，最初の文字は一致しますが，二番目の文字は異なっています．この場合も，比較対象となるテキスト内の文字 'k' がパターンに含まれていませんので，以下に示すように，再び，5 文字だけ右にずらします．
- 上の図に示した比較を行うと，先の場合のように 2 番目の文字が異なっています．しかし，先の場合とは異なり，比較対象となるテキスト内の文字 'c' はパターンに含まれています．そこで，先に作成したずらし幅の表に基づき，現在値（ k1 の値）を基準として，文字 'c' に対するずらし幅（ 2 ）だけ右にずらします（ k1 = k1 + 2 = 13 + 2 = 15 ）．
- すると，上の図に示すように，4 番目の文字が異なり，かつ，比較対象となるテキスト内の文字 'c' がパターンに含まれています．ここで，先の場合と同じように，現在地を基準として右に 2 だけずらす（ k1 = k1 + 2 = 12 + 2 = 14 ）と，4 で示した位置と一致してしまいます．このままでは，4 と 5 を繰り返し，無限ループに入ってしまいます．そこで，現在の位置から決まるずらし幅（ パターンの文字列長 - パターンの現在位置（ k2 の値 ） = 5 - 1 = 4 ）が，表から決まるずらし幅 2 より大きい場合は，現在の位置を基準にして，現在の位置から決まるずらし幅だけ右にずらします（ k1 = k1 + 4 = 12 + 4 = 16 ）．その結果，以下のような状態になります．
- 上の状態では，最初の文字が異なっており，かつ，比較対象となるテキスト内の文字 'x' がパターンに含まれていません．そのため，5 文字（パターンの文字列長）だけ右にずらします．
- 上の図からも明らかなように，この状態でパターンが見つかることになります．
- パターンに現れる文字のずらし幅を決定します．つまり，パターンに現れる各文字に対して，その文字の右側に何文字存在するかの表を作成します．同じ文字が複数回現れる場合は，最も右側の文字だけを対象とします．この例の場合は，以下のようになります．