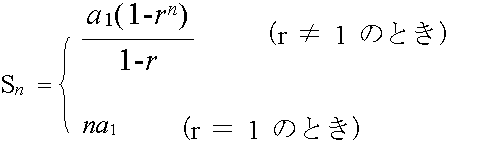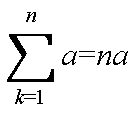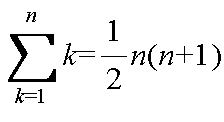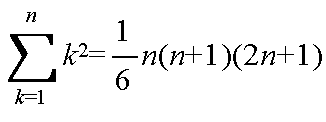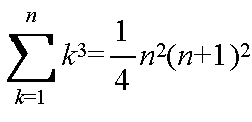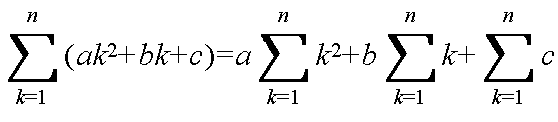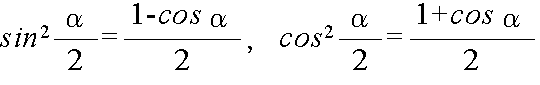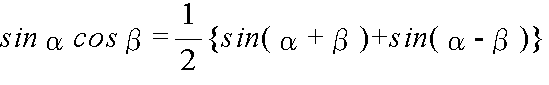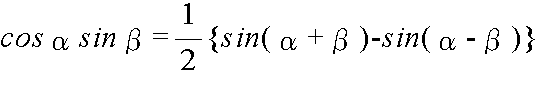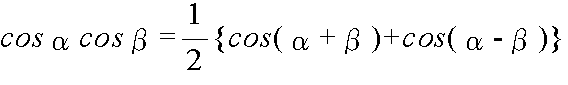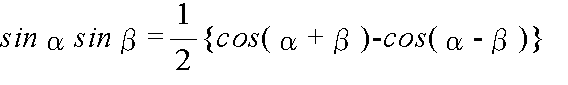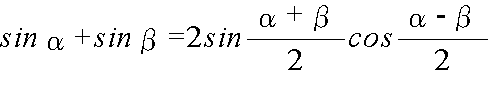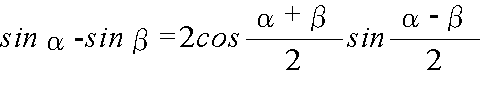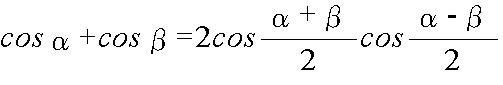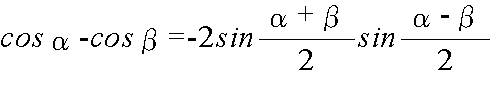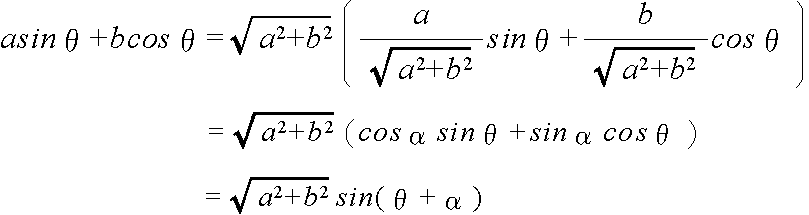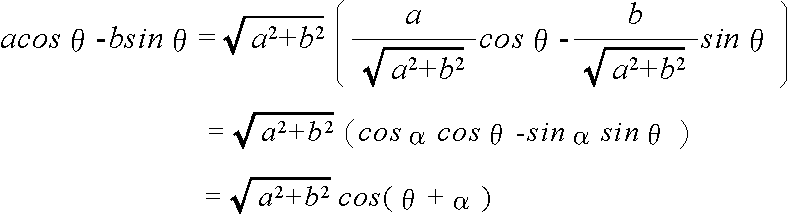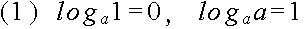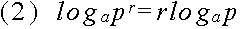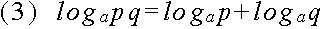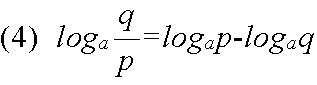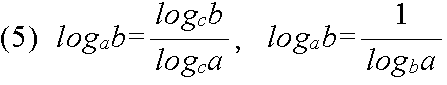
- 整数の演算
- 自然数の上だけですと,
5 - 5 3 - 5
- のような演算結果は,自然数に含まれないため,これらの演算結果を特別に扱うなど,多少不便なものになってしまいます.そこで,集合の範囲を整数( ..., -3, -2, -1, 0, 1, 2, 3, ・・・ )まで拡張すると,このような問題を避けることができます.ただし,除算に対しては,「商」と「余り」という 2 つの演算結果を対応させる必要があり,余りが 0 とならない除算を含む演算は多少面倒になります.また,0 による除算は許されません.
- べき乗(累乗) ab は,a を b 回かけること(さしあたって,ここでは,b が 0 以上の場合だけを考える),例えば,b が 3 の場合は,a × a × a を意味しています.ただし,b が 0 の場合は 1,つまり,
a0 = 1- と定義します.この定義には何か不自然さを感じるかもしれません.a を 0 回かける,つまり,1 回もかけないのだから 0 ではないかと感じる人も多いかと思います.そこで,まず,加算と減算について考えてみます.s は a を 2 回加えた結果,つまり,s = a + a であるとします.s から a を引けば,s の値は a を 1 回加えた結果 s = a になります.さらに a を引けば s の値は a を 0 回加えた結果,つまり,a を 1 回も加えない結果である s = 0 となります.この説明に疑問を感じる人はいないかと思います.
- 次に,乗算と除算について考えてみます.s は a を 2 回かけた結果,つまり,s = a × a であるとします.s を a で割れば,s の値は a を 1 回かけた結果 s = a になります.さらに a で割れば s の値は 1 になります.手続き上,これが a を 0 回かけた結果に相当することは明らかだと思います.この結果からも,a0 = 1 と定義することに不自然さがないことを理解できたと思います.
- 整数に対する加減乗除は,以下のようにして行われます.除算に対しては,余りが 0 となる場合だけを扱っていますので,商だけを示しています.結果の符号,計算の優先順位に注意して下さい.
-(-3) = 3 // 負の負は正 -(+3) = 3 // 正の負は負 +(-3) = 3 // 負の正は負 6 + (-3) = 3 // 負の数の加算 6 - (-3) = 9 // 負の数の減算 6 × (-3) = -18 // 符号に注意 -6 × (-3) = (-6) × (-3) = 18 // 符号に注意 6 ÷ (-3) = -2 // 符号に注意 -6 ÷ (-3) = (-6) ÷ (-3) = 2 // 符号に注意 (-2)3 = -8 // 負の数を奇数回かけると負 -23 = -8 // べき乗が優先 (-2)4 = 16 // 負の数を偶数回かけると正 -24 = -16 // べき乗が優先 5 + 6 × 2 = 17 // 加算,減算より乗算,除算を優先 5 - 6 ÷ 2 = 2 // 加算,減算より乗算,除算を優先 5 × 6 ÷ 2 = 15 // 同じ優先度であれば,最初から順番に実行
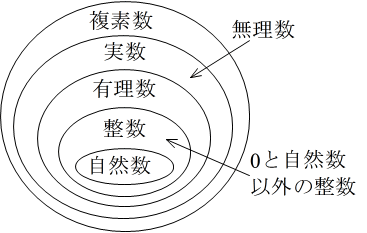
- 素数と素因数分解
- 1 より大きい整数のうち,1 と自分自身以外の整数では割り切れないような整数を素数といいます.素数を求める方法として,「エラトステネスのふるい」という有名な方法があります.その具体的な方法は,以下に示すとおりです.
- 1 は素数ではないので除く.
- 2 は素数であるので残し,2 で割り切れるものを除く.
- 3 は素数であるので残し,3 で割り切れるものを除く.
- 5 は素数であるので残し,5 で割り切れるものを除く( 4 は既に除かれている).
- ・・・・・
- 与えられた数 N が素数であるか否かを見分けるには,2 から(N - 1)までの整数で割ってみればよいことになります.もし,いずれの数でも割りきれなければ素数になります.実際には,(N - 1)まで試す必要はありません.2 から
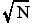 までの整数に対して調べれば十分です.
までの整数に対して調べれば十分です.
- 例えば 60 を 3 × 20 のように,2 つ以上の自然数の積で表現するとき,3 や 20 を 60 の因数と呼び,特に,素数である因数を素因数と呼びます.一般に,自然数を素数の積の形で表現すること,たとえば,60 の場合,
60 = 22 × 3 × 5
- のような形で表現することを素因数分解するといいます.
- 素数という概念にどれだけ意味があるのか,と感じる人も多いかと思います.しかし,現代社会において素数は重要な意味を持っています.上で述べた素因数分解を求める効率的な方法は現時点では見つかっていません.そのため,2 つの大きな素数によって構成される数に対する素因数分解を求めるのに,最新のコンピュータを使用しても膨大な時間がかかります.当然,素数がさらに大きくなれば,現実的には計算不可能になります.この性質を利用して,素数は暗号化に利用されています.
- 1 より大きい整数のうち,1 と自分自身以外の整数では割り切れないような整数を素数といいます.素数を求める方法として,「エラトステネスのふるい」という有名な方法があります.その具体的な方法は,以下に示すとおりです.
- 最大公約数と最小公倍数
- 2 つ以上の正の整数に共通な約数(公約数.その数で割ったとき余りが出ない数)のうち最大のものを最大公約数,また,共通な倍数(公倍数)のうち最小のものを最小公倍数といいます.以下の例に示すように,各数を素因数分解し,共通な約数をすべて掛け合わせたものが最大公約数となります.また,共通な約数に,各素因数分解の残りの部分を共通化する数を掛ければ最小公倍数となります.
- 例1: 12 = 22 × 3 = 2 × 3 × 2,18 = 2 × 32 = 2 × 3 × 3
- 最大公約数 = 2 × 3 = 6
- 最小公倍数 = (2 × 3) × 2 × 3 = 36
- 12 に 3,また,18 に 2 を掛ければ,最小公約数で割った値がいずれも 6 になる( 6 が各素因数分解の残りの部分を共通化する数)
- 例2: 12 = 22 × 3,30 = 2 × 3 × 5,15 = 3 × 5
- 最大公約数 = 3
- 最小公倍数 = (3) × 22 × 5 = 60
- 12 に 5,30 に 2,また,15 に 22 を掛ければ,最小公約数で割った値がいずれも 20 になる( 20 が各素因数分解の残りの部分を共通化する数)
- 素因数分解を行わなくても,以下のような方法によっても最大公約数や最小公倍数を求めることができます.まず,最大公約数は,すべての数に共通な数で割れるだけ割っていき,共通に割った数の積を求めることによって計算できます.最小公倍数を求める際も,共通な数で割っていきますが,すべての数に共通な数である必要はありません.2 つ以上の数に共通な数であれば,割れない数はそのままにして,割っていきます.そして,割った数と残った数をすべて掛け合わせたものが最大公倍数となります.

- 2 つ以上の正の整数に共通な約数(公約数.その数で割ったとき余りが出ない数)のうち最大のものを最大公約数,また,共通な倍数(公倍数)のうち最小のものを最小公倍数といいます.以下の例に示すように,各数を素因数分解し,共通な約数をすべて掛け合わせたものが最大公約数となります.また,共通な約数に,各素因数分解の残りの部分を共通化する数を掛ければ最小公倍数となります.
8 ÷ 7
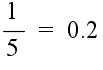
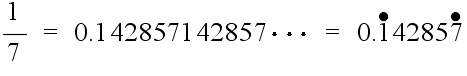

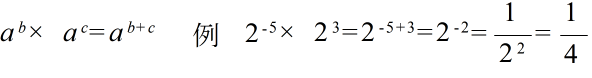
- 分数の加算と減算
- 分母が同じ場合の加算と減算は,以下の例に示すように,単に分子同士の演算を行えば結果が得られます.以下の例でも同様ですが,約分できるような結果になった場合,つまり,分母と分子の最大公約数が 1 より大きい場合は,分母と分子を最大公約数で割って(約分して)下さい.
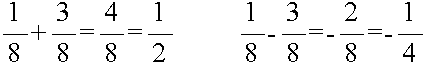
- 分母が異なる場合は,通分をして(分母を同じにして)から計算する必要があります.通分をするためには,まず,分母の最小公倍数を求めます.それが各分数の分母になります.次に,各分数の分子に,最小公倍数をその分数の分母で割った値を掛けた後,加算と減算を行います.下の左側の例はこの方法で計算しています.最小公倍数が分からない場合は,分母を掛け合わせたものを共通の分母とし,分子に対しても他の分数の分母を掛け,同様の計算を行えば同じ結果が得られます(右側の例).
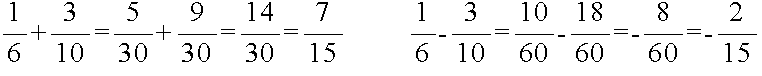
- 分数の乗算
- 乗算は非常に簡単です.分母同士,分子同士を掛け合わせれば結果が得られます.約分可能な結果になった場合は,原則として,約分します.
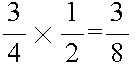
- 分数の除算
- 分数で割るということは,分数の逆数(分母と分子を入れ替えたもの)を掛けることに相当します.したがって,被除数の分母と除数の分子(結果の分母),被除数の分子と除数の分母(結果の分子)を掛け合わせれば結果が得られます.除算においても,約分可能な結果になった場合は,原則として,約分します.
- 逆数を掛けるということは,計算を簡単に行うといった点からも非常に重要です.例えば,1/10 で割るということは,10 倍するということを意味しています.また,同様に,0.1 で割ることも,10 倍するということを意味しています.
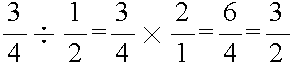
- 分数で割るということは,分数の逆数(分母と分子を入れ替えたもの)を掛けることに相当します.したがって,被除数の分母と除数の分子(結果の分母),被除数の分子と除数の分母(結果の分子)を掛け合わせれば結果が得られます.除算においても,約分可能な結果になった場合は,原則として,約分します.
- 繁分数の計算
- 繁分数とは,分数の分母や分子が分数になったものをいいます.分数とは,「分子を分母で割る」ということを意味しています.この点に注意すれば簡単に計算できます.
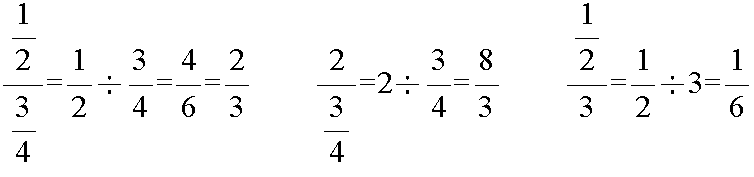
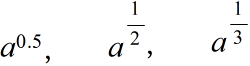
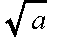 ,負の方を
,負の方を 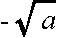 で表します.ただし,a の値が 0 の場合は,その平方根は 0 だけです.平方根は,有理数又は無理数となり,以下に示すような性質(公式)を持っています.
で表します.ただし,a の値が 0 の場合は,その平方根は 0 だけです.平方根は,有理数又は無理数となり,以下に示すような性質(公式)を持っています.
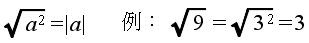
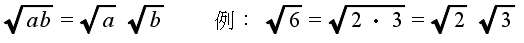
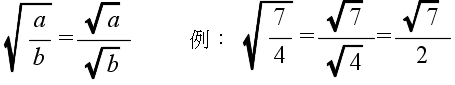
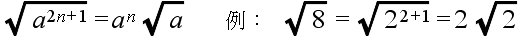
- 平方根の加算と減算
- 加算や減算は,
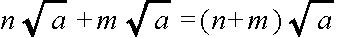
- のように,根号の中の数値が同じ場合だけ実行できます.決して,
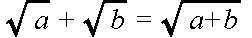 !誤り
!誤り- のようなことは行わないでください.根号の中の数値が同じでない場合であっても,たとえば下の例に示すように,根号の中に現れる数が同じになるように変形できれば,加算や減算を行うことができます.
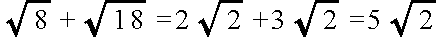
- 平方根の乗算
- 乗算の場合は,公式にもあるように,根号の中の数値が異なるどうしでも可能です.ただし,次の例にあるように,計算結果は,根号の中に現れる数が最小となる形に変形しておいてください.
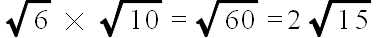
- 平方根の除算と有理化
- 除算も,基本的に,乗算と同じですが.結果によっては,分母に根号が含まれてきます.この場合,以下に示す一般形とその例のように,分母に根号を含まない形に変形できます.この処理を有理化と呼びます.
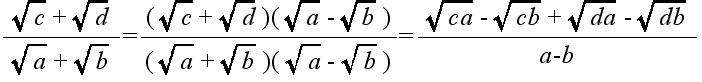
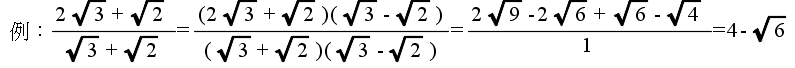
- 二重根号
- 一般に,

- の関係が成立しますので,公式,

- を使用して,以下に示す例のように,二重根号をはずすことができる場合があります.
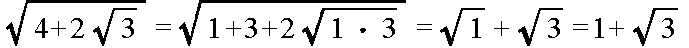
- 複素数の表現方法
- 実数の範囲では,数直線上の 0 以上の数に対してだけその平方根を計算できました.しかし,より一般的な記述を求めるとしたら,負の数に対してもその平方根を定義する必要があります.そこで,2 乗すると -1 になる数,つまり,
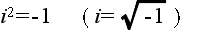
- という性質を持つ数を i で表し,虚数単位と呼ぶことにします.なお,電気系の学科では,i の代わりに j を使用しますが,意味は同じです.このようにすると,例えば,-2 の平方根も,
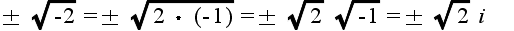
- のように記述できます.しかし,虚数単位だけでは,複素数の定義として不十分です.例えば,
x + 3 = 0 → x = -3 x2 - 3x + 2 = 0 → x = 1, 2
- のように,1 次方程式は 1 つの根,2 次方程式は 2 つの根を持ちます(重根を含む).このことを拡張して,「n 次の方程式は n 個の根を持つ」ということが言えれば都合がよいのですが,実数の範囲ではこの言明は正しくありません.例えば, x2 = 1 (1) x3 = 1 (2)
- に対して,(1) は 2 つの根( -1 と 1 )を持ちますが,(2) の根は実数の範囲では 1 だけです.(2) の他の 2 つの根は,虚数単位を導入しても,-2 の平方根のように,実数と虚数単位を掛け合わせただけの数値では表現できません.そこで,実数 a,b と虚数単位 i を使用して,
α = a + bi ( a + ib と表現する場合もある)
- のように表せる数 α を複素数と定義します.このとき,a を複素数 α の実部(実数部),b を複素数 α の虚部(虚数部)といいます.また,複素数には,以下のような性質があります.
a + bi = c + di ⇔ a = c,かつ,b = d a + bi = 0 ⇔ a = 0,かつ,b = 0
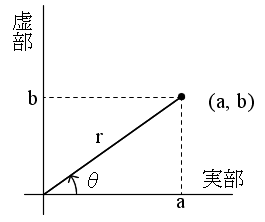
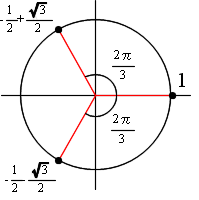
- 複素数は,その定義からも明らかなように,実部と虚部が存在するため,1 つの数直線上の点に対応させることはできません.実部と虚部の各々に対して独立な数直線が必要です.つまり,右図に示すような平面(複素平面)上の点に対応させることになります.
- 右図からも明らかなように,原点からの距離 r,
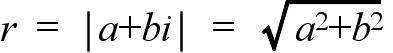
- を利用して,複素数 α は,
a + bi = r cosθ + r sinθ i = r ( cosθ + i sinθ )
- のような表現方法も可能です.この形式を複素数 α の極形式,r を複素数 α の絶対値,及び,θ を複素数 α の偏角と呼びます.
- 複素数の演算
- 複素数の加算と減算では,実部同士,虚部同士でしか演算ができません.一般的な方法は以下のようになります.
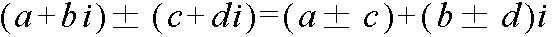
例: (2 + 3i) + (2 - i) = (2 + 2) + (3 - 1)i = 4 + 2i
- 乗算においては,実部と虚部の演算が可能です.ただし,i2 が現れると -1 に変換する必要があります.
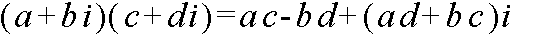
例: (2 + 3i) (2 - i) = 2 × 2 - (2 × 1) i + (3 × 2) i - (3 × 1) i2 = 7 + 4i
- 除算では,分数の形になりますが,平方根の有理化と同じように,以下に示す方法によって,分母に複素数を含まない形に変換できます(複素数の有理化).なお,複素数 a + bi (または,a - bi)に対して,複素数 a - bi (または,a + bi)を共役な複素数といいます.
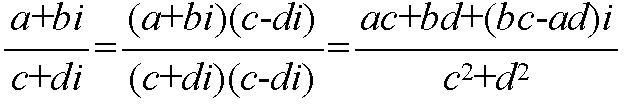
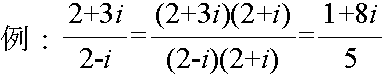
- ド・モアブルの定理
- 複素数 x = r ( cosθ + i sinθ ) に対し,
xn = rn ( cos nθ + i sin nθ )
- をド・モアブルの定理と呼びます.ここで,先に述べた「 x3 = 1 」の根をド・モアブルの定理を使って求めてみます.x の絶対値は 1 ですので r = 1 となり,
x3 = cos 3θ + i sin 3θ = 1
- を満たす θ を求めればよいことになります.具体的には,右辺の実部が 1,虚部が 0 ですので,
cos 3θ = 1,sin 3θ = 0
- を満たす θ を求めればよいことになります.従って,θ の値は,0,2π/3,4π/3 となり,次の 3 つが根になります.図で示せば,上の右に示す図のようになります.
- x = 1
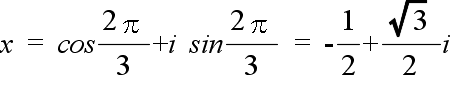
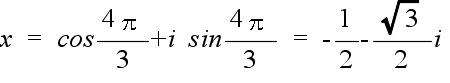
- n 進法による表現方法
- 我々は,通常,数値を表すのに 10 進法を使用します.10 進法では,0 から 9 までの 10 個の記号を使用し,10 毎に桁上がりが生じます.また,各桁はその桁に対応した 10 のベキ乗の重みを持っており,たとえば,365 は,以下のような意味を持っています.
365 = 3 × 102 + 6 × 101 + 5 × 100
- しかし,常に 10 進法を使用しているわけではありません.たとえば,60 秒 = 1分,60 分 = 1 時間のように,60 進法を使用する場合もあります.一般に,n 進法では,0 から (n-1) までの数字を使用して,数値を以下のように表現します.
a2a1a0 = a2 × n2 + a1 × n1 + a0 × n0 0 ≦ ai ≦ (n-1)
- たとえば,7 進法で表現された 365 は,
365 = 3 × 72 + 6 × 71 + 5 × 70
- のような意味を持っており,10 進法の 194 に相当します.
- n 進法,10 進法相互の変換
- 10 進法の数値を n 進法で表現するは,10 進法で表された数値を n で割っていき,その際に生じた余りを下から順に並べることによって得られます.たとえば,10 進法の 194 を 7 進法で表現した結果( 365 )を求める場合は以下のようになります.
7)194 7) 27 ・・・ 余り 5 7) 3 ・・・ 余り 6 0 ・・・ 余り 3
- 逆に,n 進法を 10 進法に変換するには,n 進法の定義式を使用して計算します.従って,n 進法を m 進法に変換するには,まず,n 進法を 10 進法の数値に変換した後,上記の方法で m 進法の数値に変換します.たとえば,8 進法の 302 を 7 進法の数値に変換する際は以下のようになります.
8 進法の 302 = 3 × 82 + 0 × 81 + 2 × 80 = 10 進法の 194 10 進法の 194 = 7 進法の 365 (上記の方法による)
- コンピュータを扱う分野では,2 進法または 16 進法がよく使用されます.2 進法では数値を 0 と 1 だけで,また,16 進法では,0~9,A,B,C,D,E,F の 16 個の文字を使用して表現します( A~F は,小文字でも構わない).例えば,10 進法の 0~15 は,以下のように表現されます( 10 進法,2 進法,16 進法の順).
0 0000 0 1 0001 1 2 0010 2 3 0011 3 4 0100 4 5 0101 5 6 0110 6 7 0111 7 8 1000 8 9 1001 9 10 1010 A 11 1011 B 12 1100 C 13 1101 D 14 1110 E 15 1111 F
3ax2,5y
3ax2 - 4bx + 5 (1)
- 加法と減法
- 整式の加法や減法においては,次の例に示すように,同類項(係数を除いて,文字の部分が同じである項)の間だけで演算が可能である点に注意して下さい.
(-x2 + 3x - 5) + 2(x2 - 5x + 2) = (-1 + 2)x2 + (3 - 10)x + (-5 + 4) = x2 - 7x - 1
- べき乗(累乗)
- べき乗(累乗)とは,整数の演算に関する説明でも述べたように,同じ項を複数回掛ける操作をいいます.たとえば,2x の 3 乗とは,2x を 3 回掛ける操作,つまり,「 2x × 2x × 2x 」を表し,「 (2x)3 」のように表現します.ここで,「 3 」 の部分を,指数と呼びます.べき乗に関しては,以下のような性質があります.
xmxn = xm+n 例: x2x3y = x5y (xy)n = xnyn (xm)n = xm×n 例: (x2y)3 = x6y3
- では,xn において,n の値が 0 や負になった場合はどうなるのでしょうか( x は 0 でないとする).たとえば,x3 を x で割っていく( 1/x 倍していく)と,以下のように変化していきます.
x3 → x2 → x1 = x
- このように,1/x を掛ける毎に n の部分が 1 づつ減っていきます.この規則を n の値が 0 や負になる場合にも適用します.上の結果に 1/x を掛ければ 1 になり,さらに,1/x を掛けていけば,1/x,1/x2,・・・のように変化していきます.そこで,指数が 0 又は負になる場合に対して,以下のように定義します.

- 乗法
- 乗法においては,加法や減法とは異なり,任意の項同士の演算が可能です.従って,整式の乗算は,以下の例に示すように,各項のすべての組み合わせに対して実行されます.そして,その結果は,同類項をまとめて(同類項同士の加算や減算を実行して)表現します.
(-x2 + 3x - 5) (x2 - 5x + 2) = (-x2)(x2) + (-x2)(-5x) + (-x2)(2) + (3x)(x2) + (3x)(-5x) + (3x)(2) + (-5)(x2) + (-5)(-5x) + (-5)(2) = -x4 + 5x3 - 2x2 + 3x3 - 15x2 + 6x - 5x2 + 25x - 10 = -x4 + (5 + 3)x3 + (-2 - 15 - 5)x2 + (6 + 25)x - 10 = -x4 + 8x3 - 22x2 + 31x - 10
- 因数分解
- 例えば,x2 + 4x は,
x2 + 4x = x(x + 4)
- のように,x と x + 4 の積で表現できます.このように,1 つの多項式が複数の整式(単項式又は多項式)の積で表現できるとき,各整式を元の多項式の因数と呼びます.また,多項式をいくつかの因数の積の形で表現することを因数分解といいます.乗法に対する例では,多項式の積の形を項の和の形に変換しました(これを,展開と呼ぶ)が,因数分解はその逆の操作に当たります.因数分解では,たとえば,以下に示すような公式等を利用します.
- 共通因数でくくる
- 例: 2x2 + 8xy = 2x(x + 4y)
- 2 次式に対する公式の利用
- (x ± y)2 = x2 ± 2xy + y2
- 例: x2 + 6x + 9 = (x + 3)2 x が x,y が 3 に相当
- (x + y) (x - y) = x2 - y2
- 例: 4x2 - 9 = (2x + 3)(2x - 3) x が 2x,y が 3 に相当
- (x + a) (x + b) = x2 + (a + b)x + ab
- 例: x2 + x - 6 = (x + 3)(x - 2) a,b が 3,-2 に相当
- (ax + b) (cx + d) = acx2 + (ad + bc)x + bd
- 例: 2x2 + 7x + 3 = (2x + 1)(x + 3) a が 2,b が 1,c が 1,d が 3 に相当(ac = 2, ad + bc = 7, bd = 3 を満たすa, b, c, d を見つけて因数分解する)
- (x ± y)2 = x2 ± 2xy + y2
- 3 次式に対する公式の利用
- (x + y) (x2 - xy + y2) = x3 + y3
- (x - y) (x2 + xy + y2) = x3 - y3
- 例: x3 - 8 = (x - 2) (x2 + 2x + 4) x が x,2 が y に相当
- 例: x3 + 1 - 2x(x + 1)
- = (x + 1) (x2 - x + 1) - 2x(x + 1)
- = (x + 1) (x2 - x + 1 - 2x)
- = (x + 1) (x2 - 3x + 1)
- (x + y)3 = x3 + 3x2y + 3xy2 + y3
- (x - y)3 = x3 - 3x2y + 3xy2 - y3
- (x + y + z) (x2 + y2 + z2 - xy - yz - zx) = x3 + y3 + z3 - 3xyz
- (x + y) (x2 - xy + y2) = x3 + y3
- 置き換えを利用する
例: (x + a)2 + 2b(x + a) + b2 y = (x + a) とおく
= y2 + 2by + b2
= (y + b)2
= (x + a + b)2 元に戻す - 因数定理(後述)を利用する
(4x2y3 - 3y2 + xy) ÷ xy = 4xy2 - 3x-1y + 1
(x3 - 3x + 4) ÷ (x2 + 2x - 5) → 商: x - 2, 余り: 6x - 6 ∴ (x3 - 3x + 4) = (x2 + 2x - 5) (x - 2) + (6x - 6)
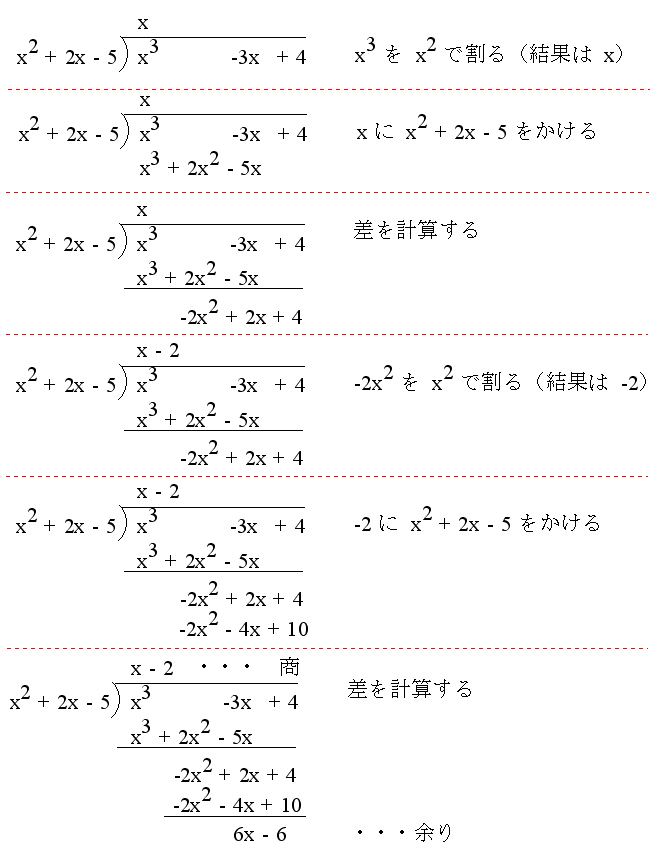
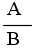
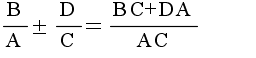
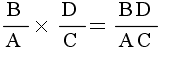
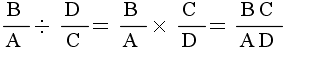
- 共通因数を利用した計算例
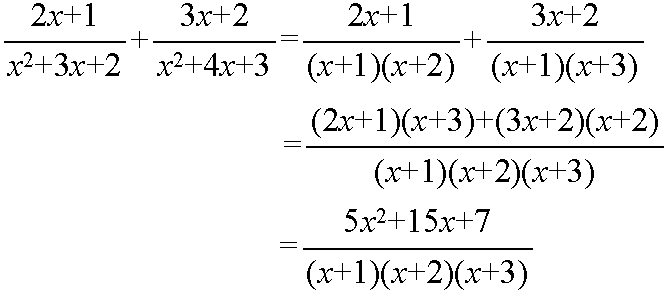
- 共通因数を利用しない計算例
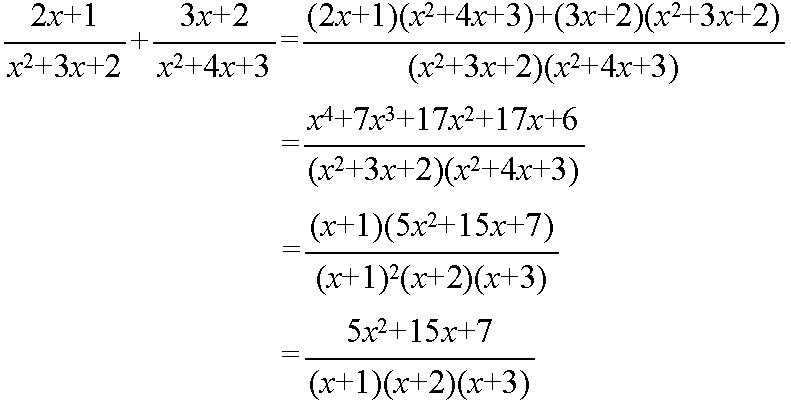
x ≧ 0 のとき |x| = x, x < 0 のとき |x| = -x
|x| ≧ 0 ( 0 となるのは,x = 0 のときに限る) |-x| = |x|
x + 5 ≧ 0,つまり,x ≧ -5 のとき: |x + 5| = x + 5 x + 5 < 0,つまり,x < -5 のとき: |x + 5| = -(x + 5) = -x - 5
4x = 100 (1)
2(x + y) = 100 (2)
y = x + 10 (3)
- 1 次方程式
- 1 次方程式とは,方程式を構成する各項の次数の最大値が 1 である方程式です.同様に,最大次数が n である場合は,n 次方程式と呼びます.1 次方程式,
ax + b = 0
- は,a ≠ 0 のときに限って解を持ち,その解は,
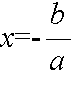
- となります.
- 式の中に絶対値記号を含む場合は,絶対値記号を外してから解く必要があります(「絶対値記号を含んだ式」参照).例えば,
|ax + b| = c
- は,「ax + b」の正負によって,次に示すいずれかの式で記述され,2つの解が得られます.
ax + b > 0 のとき.ax + b = c ∴ x = (c - b) / a ax + b < 0 のとき.-ax - b = c ∴ x = -(c + b) / a
- 1 次不等式
- 不等式とは,等式における等号を大小関係を表す不等号に置き換えた式です.方程式を解く場合と同様,大小関係が成立する変数の値(の範囲)を求めることを不等式を解くといいます.1 次不等式を解く際も,上と同様に方程式の解を求める必要があります.しかし,不等式に対しては,両辺に定数を掛けたり,または,両辺を定数で割る場合,定数が負であると,不等号の向きが変わる点に注意してください.1 次不等式の場合は,以下のようになります.
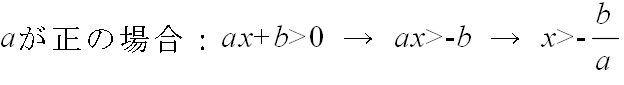
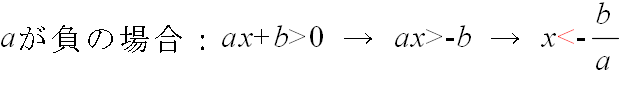
- 式の中に絶対値記号を含む場合は,1 次方程式の場合と同様,絶対値記号を外してから解く必要があります(「絶対値記号を含んだ式」参照).
- [参考] 1 次方程式
- ax + b = 0
- を解くことは,1 次関数
- y = ax + b
- の x 軸との交点を求めることに相当します.a = 0 は,1 次関数の傾きが 0,つまり,x 軸と平行である場合になります.同様に,1 次不等式では,1 次関数の値が正(負)になる x の範囲を求めることになります.(後述する「関数と方程式・不等式」参照)
- 2 次方程式
- 2 次方程式 ax2 + bx + c = 0 の解は,判別式,
D = b2 - 4ac
- の値によって,次のように,重解(重根),実数解(実根),または,虚数解(虚根)のいずれかになります.
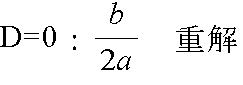
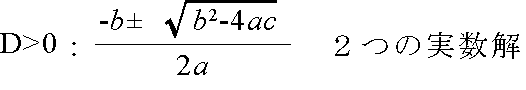
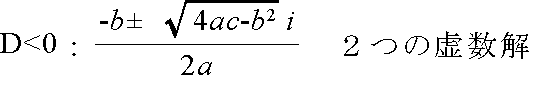
- 2 次方程式 ax2 + bx + c = 0 の 2 つの解を α,β とします.これらの解と 2 次方程式の係数間には以下のような関係があります(根と係数の関係).
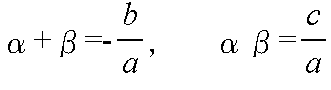
- 逆に,α と β を 2 つの解とする 2 次方程式は,
(x - α)(x - β) = 0 ∴ x2 - (α + β)x + αβ = 0
- となります.したがって,α + β = p,αβ = q とすると,α と β は,次の 2 次方程式の解となります.
x2 - px + q = 0
- 高次方程式
- 3 次及び 4 次方程式に対して,2 次方程式のような公式を使って(解析的に)解を求めることはできますが非常に面倒なものになります.さらに,5 次以上の高次方程式に対しては,一般に解析的に解を求めることはできません.必要とする場合は,コンピュータによって数値的に解を求めることになります(「ベアストウ法」参照).
- しかし,以下に示すような整式の性質を利用して簡単に解を求めることができる場合もあります.整式 A(x) を 0 でない整式 B(x) で割った商を Q(x),余りを R(x) とすると,次の関係が成立します.
A(x) = B(x)Q(x) + R(x)
- たとえば,f(x) = x3 + ax2 + bx + c を (x - α) で割ったときは,
f(x) = (x - α)Q(x) + R(x)
- のように表現できます.この式に α を代入すると,第 1 項は 0 となるので,f(α) ( = R(α)) は (x - α) で割ったときの余りになります.従って,f(α) が 0 になることは,余りが 0 であることを意味し,f(x) が (x - α) で割り切れる,つまり,α が f(x) = 0 の1つの解であることを意味します.これを,因数定理と呼びます.
- 因数定理を利用することによって,たとえば,3 次方程式,
f(x) = x3 - 6x2 + 11x - 6 = 0
- の解を求めることができます.f(1) = f(2) = f(3) = 0 ですので,(x - 1),(x - 2),及び,(x - 3) が上式の左辺の因数となります.つまり,上式の左辺が以下のように因数分解できることを意味し,結局,x = 1, 2, 3 が上に示した方程式の解になります.
(x - 1)(x - 2)(x - 3) = 0
- 3 次及び 4 次方程式に対して,2 次方程式のような公式を使って(解析的に)解を求めることはできますが非常に面倒なものになります.さらに,5 次以上の高次方程式に対しては,一般に解析的に解を求めることはできません.必要とする場合は,コンピュータによって数値的に解を求めることになります(「ベアストウ法」参照).
- 2 次不等式
- 2 次不等式,
ax2 + bx + c > 0 (1)
- に対しても,不等号を等号にした 2 次方程式の判別式が重要になってきます.判別式が負であれば,
x2 + x + 1 > 0
- のように,任意の x に対して不等式を満足するか,または,
-x2 + x - 1 > 0
- のように,不等式を満足する x の値はなくなります.
- また,判別式の値が 0 であれば,
x2 - 2x + 1 > 0 ( ≧ )
- のように,x = 1 を除く任意の x に対して不等式を満足するか(括弧内のように,等号が含まれる場合は,x = 1 に対しても不等式を満足する),または,
-x2 + 2x - 1 > 0 ( ≧ )
- のように,不等式を満足する x の値はなくなります(括弧内のように,等号が含まれる場合は,x = 1 に対してだけ不等式を満足する).
- 判別式の値が正の場合は,2 次方程式の 2 つの解を x1,x2 ( x1 < x2) とすると,2 次不等式 (1) の解は以下のようになります.
x1 < x < x2 a > 0 の場合 x < x1,または,x > x2 a < 0 の場合
- 式の中に絶対値記号を含む場合は,1 次方程式の場合と同様,絶対値記号を外してから解く必要があります(「絶対値記号を含んだ式」参照).
- [参考] 2 次方程式
- ax2 + bx + c = 0
- を解くことは,2 次関数(放物線)
- y = ax2 + bx + c
- の x 軸との交点を求めることに相当します.判別式が正の場合は x 軸と 2 点で交わること,0 の場合は頂点が x 軸に接すること,また,負の場合は,x 軸と交わらないことを意味します.一般に,高次方程式において,実数解の数は,高次方程式に対応する関数の x 軸との交点の数に相当します.2 次不等式では,2 次関数の値が正(負)になる x の範囲を求めることになります.(後述する「関数と方程式・不等式」参照)
- 連立方程式
- n 個の方程式,
f1(x, y, ・・・) = 0 f2(x, y, ・・・) = 0 ・・・・・
- をすべて満たす変数 x,y,・・・ を求めることを連立方程式を解くといいます.ただし,ここでは,すべての方程式が 1 次方程式である場合(線形連立方程式,連立 1 次方程式)と,1 つの 1 次方程式と 1 つの 2 次方程式からなる場合だけを扱います.なお,一般に,変数の数と方程式の数は一致している必要があります.
- 最初に,すべての方程式が 1 次方程式である場合について考えてみます.3 変数の場合は,例えば,以下に示すような方程式になります.このような方程式を,3 元線形連立方程式(3 元連立 1 次方程式)と呼びます.一般的に,変数の数が n の場合は,n 元線形連立方程式(n 元連立 1 次方程式)と呼びます.
2x + 4y - 2z = 4 (1) 2x + y + z = 7 (2) x + y + z = 6 (3)
- この方程式を解くためには,1 変数だけからなる式を導出してやる必要があります.連立方程式においては,方程式の両辺に定数を乗じ,他の方程式との加算や減算を行っても連立方程式の内容は変化しません.この性質を利用して,例えば,変数 x を消去します.まず,(1) 式から (2) 式を引くと以下のような式が導出されます.
3y - 3z = -3 (4)
- また,(3) 式を 2 倍して (2) 式から引くと以下の式が得られます.
-y - z = -5 (5)
- (5) 式より y = 5 - z という結果が得られますので,これを (4) 式に代入すると,以下に示すように,z だけを含む 1 次方程式となり,z の値を求めることができます.
3(5 - z) - 3z = -3 ∴ z = 3
- この結果,(5) 式より,y は 2 となり,これらの結果を (1),(2),又は,(3) 式に代入すれば,x = 1 が求まります.
- 先に述べたように,n 変数の場合は n 個の方程式が必要ですが,単に n 個あればよいというわけではありません.n 個の方程式に連立方程式を解くために必要な情報が含まれていなければなりません.例えば,2変数の場合,
2x + y = 4 (6) 4x + 2y = 8 (7)
- を満足する解は無限に存在します.(6) 式の両辺を 2 倍してみれば明らかなように,2 つの式は全く同じ式であるため,x と y を一意に決めるための情報が不足しています.また,
2x + y = 3 (8) 4x + 2y = 8 (9)
- や
x + y = 3 (10) x + 2y = 8 (11) x - 2y = 5 (12)
- に対しても解を求めることができません.いずれの場合も,すべての式を同時に満たす x,y は存在しません.
- 次に,1 次方程式と 2 次方程式からなる連立方程式
dx + fy = g (13) y = ax2 + bx + c (放物線) (14) 又は (x - x0)2 + (y - y0)2 = r2 (円) 又は xy = k (双曲線)
- について考えてみます.いずれの場合も,(13) 式から x 又は y を求め,それを (14) 式に代入すれば x または y に関する2次方程式が得られます.したがって,2 次方程式に対する公式を使用すれば簡単に解を求めることができます.
- 連立不等式
- 連立方程式で述べた式において,等号を不等号に置き換えれば連立不等式になります.ここでは,
a1x + b1 > 0, a2x + b2 > 0, ・・・ (15) dx + e > 0, ax2 + bx + c > 0 (16)
- のような 2 つのタイプの連立不等式だけについて検討します.いずれの場合も,各 1 次方程式又は 2 次方程式を先に述べた方法で解き,それらの共通部分が解になります.
- 例えば,
x + 2 > 0, x - 3 < 0
- の解は,
-2 < x < 3
- となり,
x > 0, x2 - x - 2 < 0
- の解は,
0 < x < 2
- となります.
- [参考] 線形連立方程式の場合,各方程式で表される直線(平面)の交点を求めることに相当します.(8),(9) 式の場合は,2つの直線が平行になり,交点がありません.また,(10),(11),(12) 式の場合は,3 直線が 3 つの点で交わり,すべての直線が同時に通るような点は存在しません.
- (15),(16) 式の場合は,直線と放物線(円,双曲線)との交点を求めることに相当します.虚数解になる場合は,交点が存在しない(交わらない)ことを意味しています.また,重根の場合は,直線が放物線(円,双曲線)に接することを意味しています.(後述する「関数と方程式・不等式」参照)
- 鶴亀算 鶴と亀が合わせて 10 匹います.足の数は,合わせて 28 本です.鶴は何匹ですか.
- 方法1: 鶴を x 匹,亀を y 匹とすると,
x + y = 10 匹数 2x + 4y = 28 足の数
- 方法2: 鶴を x 匹とすると,
2x + 4(10 - x) = 28 足の数
- 速度算 学校まで行きは時速 5 km で歩いたが,帰りは時速 4 km で歩いたので,30 分余分にかかりました.学校までの距離は何 km ですか.
- 方法1: 学校までの距離を x km とすると,
x / 4 - x / 5 = 0.5 かかった時間の差
- 方法2: 行きに学校までかかった時間を x 時間とすると,
5x = 4(x + 0.5) 左辺も右辺も学校までの距離
- 通過算 列車が長さ 5190 m のトンネルを通過するのに 182 秒,また,長さ 5760 m のトンネルを通過するのに 201 秒かかりました.列車の長さは何 m ですか.
- 列車の長さを x m,列車の速さを y m/秒とおくと,
(x + 5190) ÷ y = 182 長さ 5190 m のトンネル通過時間 (x + 5760) ÷ y = 201 長さ 5760 m のトンネル通過時間
- 損益算 ある品物を 100 個仕入れ,原価に対して 2 割の利益を見込んで定価を付けるつもりです.4000 の利益を得るためには,1 個いくらで仕入れればよいでしょうか.ただし,品物は全部売れるものとします.
- 原価を x 円とすると,
100 × 1.2x - 100x = 4000 得られる利益
- 仕事算 ある仕事を鈴木さんが一人ですれば 20 日かかります.同じ仕事を山田さんがすれば 10 日かかります.鈴木さんがこの仕事を始め,途中で山田さんに替わったところ,全部で 15 日かかりました.鈴木さんが働いたのは何日でしょうか.
- 鈴木さんが働いた日数を x 日とすると,鈴木さん及び山田さんが1日に行う仕事量は,それぞれ,1/20 及び 1/10 ですので,
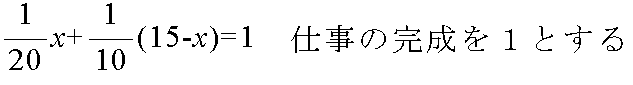
- 水槽算 ある水槽を満たすのに,A 管だけで 15 分,B 管だけで 10 分かかります.2 管を同時に使用した場合何分かかりますか.
- 水槽を満たすまでの時間を x とおくと,
(1 / 15 + 1 / 10)x = 1
- 時計算 1 時から 2 時の間で,時計の長針と短針が重なるのは何時何分ですか.
- 1 時のとき,12 時の位置から見て,長針は 0 度の位置,短針は 30 度の位置にあります.また,長針は 1 分間に 6 度,短針は 0.5 度動きます.1 時から x 分後に重なるとすると,
6x = 30 + 0.5x 長針の位置 = 短針の位置
- 年齢算 現在,太郎君の年齢は 5 歳で,お父さんの年齢は 30 歳です.お父さんの年齢が太郎君の年齢の 2 倍になるのは何年後でしょうか.
- x 年後に 2 倍になるとすると,
(5 + x) = 30 + x 右辺が x 年後のお父さんの年齢
- 流水算 ある川において,12 km 離れた地点を舟で往復するのに,上りは 3 時間,下りは 2 時間かかりました.川の流れの速さは時速何 km でしょうか.
- 舟の速さを時速 x km,流れの速さを時速 y km とすると,
3(x - y) = 12 上り 2(x + y) = 12 下り
- 濃度算 1 %の食塩水 100 g と,3 %の食塩水 300 g を混ぜると何%の食塩水になるでしょうか.
- x %の食塩水になるとすると,
0.01 × 100 + 0.03 × 300 = 400 × 0.01x 左辺も右辺も食塩の量(食塩の量は変化しない)
- 植木算 100 m ある道路の両側に 5 m おきに木を植えることになりました.道路の最初と最後にも植えるとすると,木は何本必要でしょうか.
- 木の本数を x 本とすると,
x = 2 × (100 ÷ 5 + 1)
ax2 + 3bx + c = 9x + 3
a = 0 右辺に x2 を含む項がない 3b = 9 c = 3
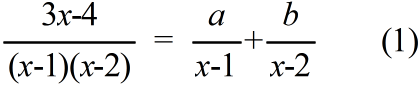
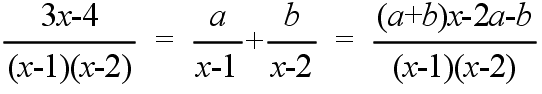
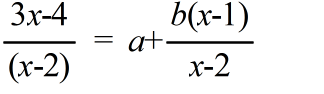
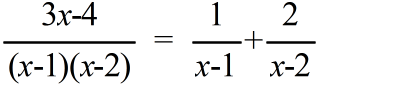
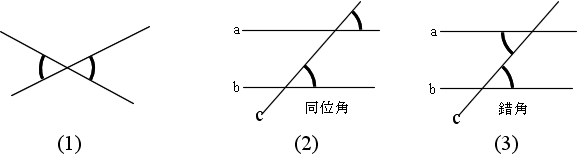
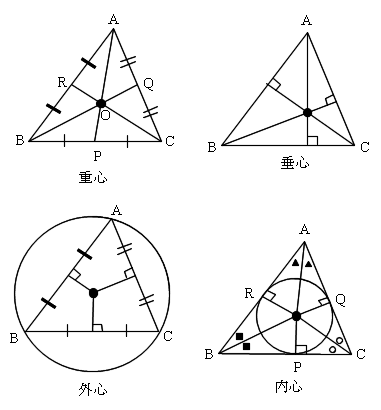
AO : OP = 2 : 1 BO : OQ = 2 : 1 CO : OR = 2 : 1
AR = AQ, BP = BR, CQ = CP
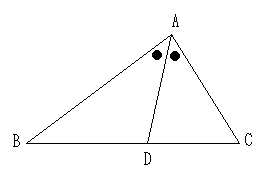
BD : DC = AB : AC
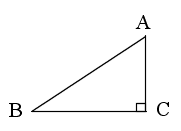
AB2 = BC2 + CA2
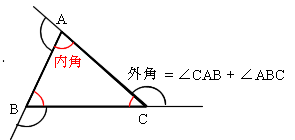
・外角の和 = 360 度
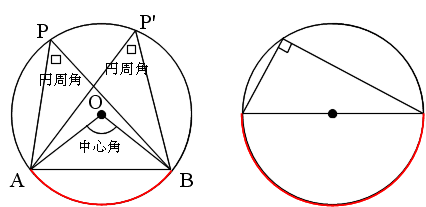
・同じ弧に対する円周角は等しい(右の左図)
・半円の弧(中心角が 180 度)に対する円周角は 90 度(右の右図)
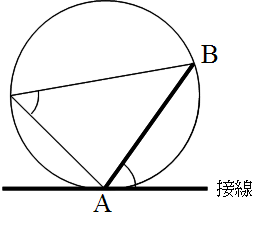
- 3 組の辺がそれぞれ等しい
- 2 組の辺とその挟む角がそれぞれ等しい
- 1 組の辺とその両端の角がそれぞれ等しい
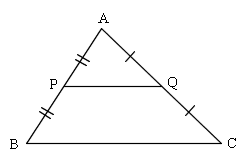
- PQ : BC = 1 : 2
- △APQ の面積 : △ABC の面積 = 1 : 4
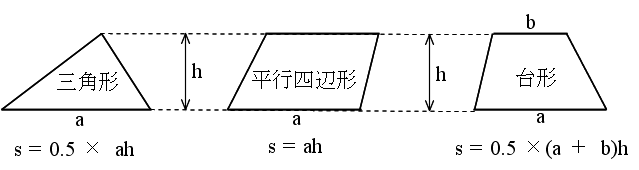
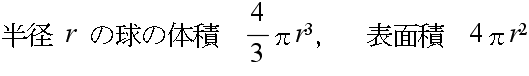
・立体 A と立体 B の体積の比 a3 : b3
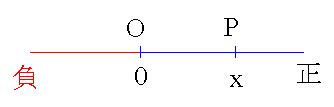
- 数直線と座標
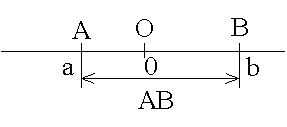
- 直線上に基準点 O をとり,単位の長さを決めると,直線上の点と実数とを対応させることができます.この直線を数直線,O を原点,また,数直線上の点 P に対応する実数 x を点 P の座標といい,点 P の座標が x であることを P(x) と表します.点 P は,x が 0 なら原点,x が正なら原点より右,また,負なら原点より左に位置することになります.
- 点 A(a) と点 B(b) の距離 AB は,絶対値を使用して,
AB = |a - b| = |b - a|
- となります.特に,原点までの距離は,座標の絶対値 |a| や |b| で表現できます.
- 内分点と外分点
- 線分 AB (点 A の座標を a,点 B の座標を b とする)を下に示すように分割する点 P を,線分 AB の内分点といいます.
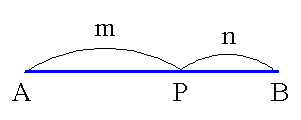
- 内分点に対しては,AP : PB = m : n が成立しますので,点 P の座標を x とすると,
(x - a) : (b - x) = m : n
- という関係から,その座標は下のようになります.なお,線分 AB の中点は,m = n = 1 となる内分点の特別の場合であり,その座標は下図の括弧内のようになります.
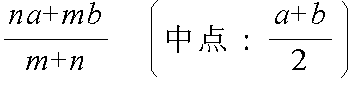
- 同様に,線分 AB を以下に示すように分割する点 P を,線分 AB の外分点といいます.

- 外分点に対しても,AP : PB = m : n が成立しますので,点 P の座標を x とすると,
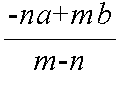
(x - a) : (x - b) = m : n
- という関係から,その座標はその右のようになります.
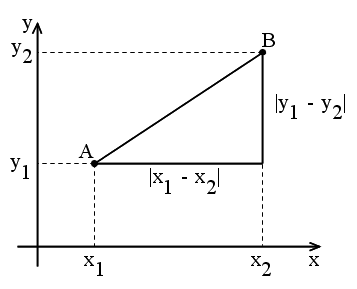
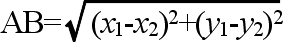
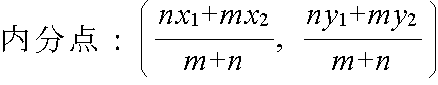
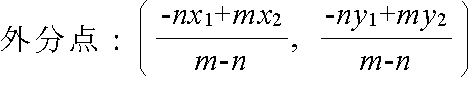
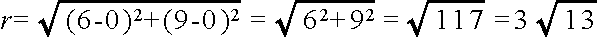
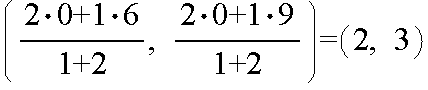
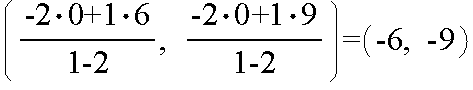
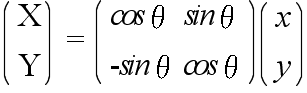
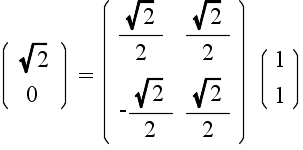
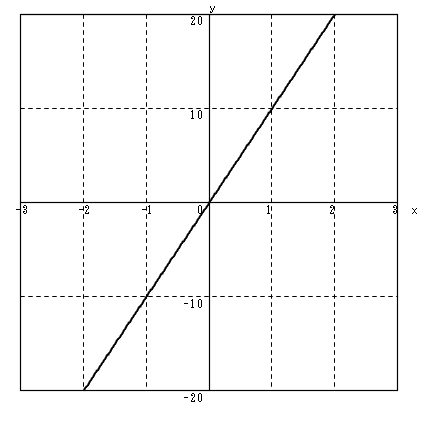
y = 10x (1)
y = ax (2)
y = 20 / x ∴ xy = 20 (3)
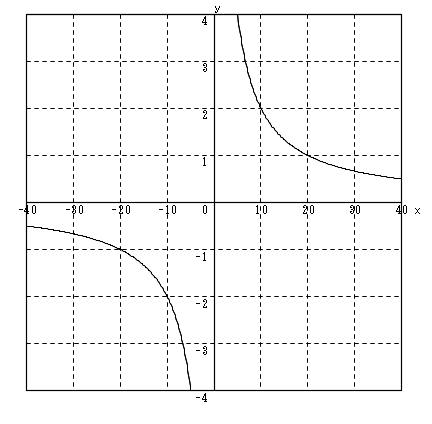
y = a / x ∴ xy = a (4)
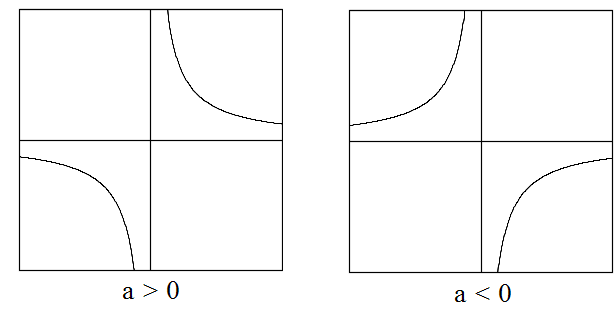
- 直線の方程式
- 2 つの変数 x 及び y の間の関係が式で表現されているとき,y は x の( x は y の)関数であるといいます.特に,x 及び y の最高位の次数が 1 であるとき,y は x の( x は y の) 1 次関数であるといいます.1 次関数は,一般的に,
ax + by + c = 0 (1)
- のように表現でき, x と y の関係を図示すれば,下に示すような直線になります.
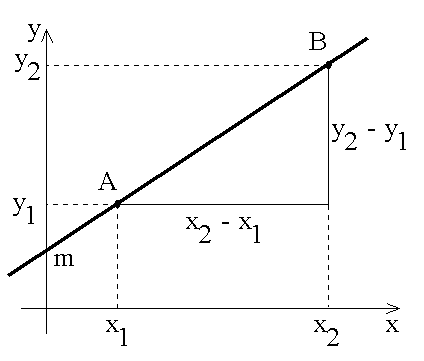
- (1) 式は,b ≠ 0 である場合,以下のように書き直すことができます.
y = kx + m (2)
- ただし,
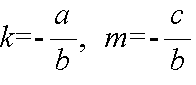
- とします.このとき,k を直線の傾きといい,直線上のどんな異なる 2 点 A(x1, y1),B(x2, y2) をとっても,傾き,
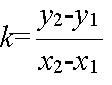
- の値は一定です.また,m を y 切片と呼び,直線と y 軸との交点の座標を表します.また,(2) 式は,(y - m ) が x に比例することを表現しているとみなすこともできます.
- a = 0 のときは,傾きが 0 になり,x 軸に平行な直線となります.また,b = 0 で,かつ,a ≠ 0 の場合は,(1) 式は次のように変形でき,y 軸に平行な直線となります.
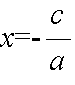
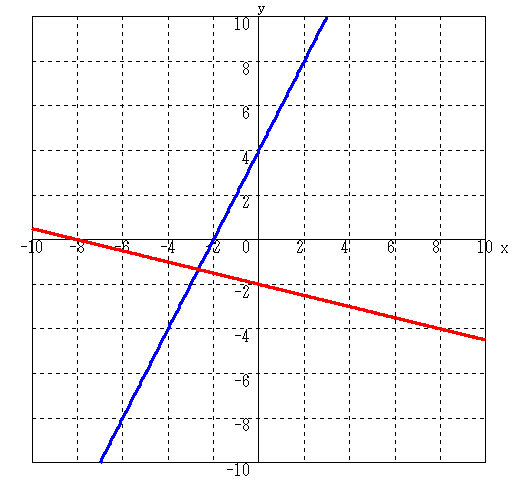
- 例えば,下図における青色の直線は,傾きが 2,y 切片が 4 の直線,
y = 2x + 4
- を,また,赤色の直線は,傾きが -0.25,y 切片が -2 の直線,
y = -0.25x - 2
- を表しています.
- 傾きと y 切片が決まれば,対応する直線も一意に決まります.そのほか,以下のようなデータが与えられても,直線の方程式を一意に決めることができます.
- 1 点と傾き: 点 A(x1, y1) を通り,傾きが k である直線の方程式は以下のようになります.
y - y1 = k (x - x1)
- 2 点: 2 点 A(x1, y1),B(x2, y2) を通る直線の方程式は以下のようになります.
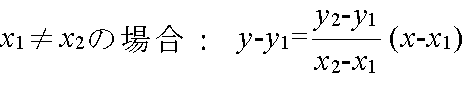
x1 = x2 の場合: x = x1
- 最大値と最小値
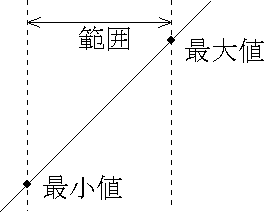
- x の範囲が指定されなければ,一般に,1次関数は最大値も最小値も持ちません( x 軸に平行な直線以外は,すべて,無限大).しかし,x の範囲が指定された場合は,その両端で最大値または最小値をとります(上図参照).
- 2 直線の関係
- 2 直線 y = k1x + m1 と y = k2x + m2 の間には,以下に示すような関係が成立します.
・k1 = k2 → 2直線が平行 ・k1k2 = -1 → 2直線が垂直(直交)
- 例えば,点 (1, 0) を通り,直線 y = x + 1 に垂直な直線の方程式は,点 (1, 0) を通り,傾きが -1 である直線の方程式ですから,以下のようになります.
y = -x + 1
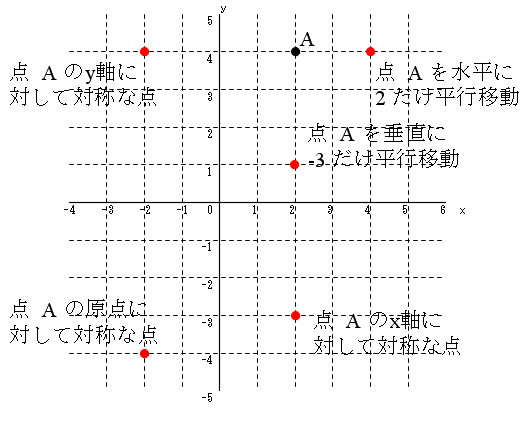
- 点と直線
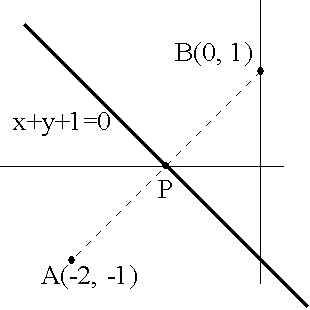
- 点と直線との関係も重要です.たとえば,直線 x + y + 1 = 0 に関して,点 A(-2, -1) と対称な点 B(x, y) の座標を求めることについて考えてみます(上図参照).直線に関して対称ですので,線分 AB の中点が直線上に存在するはずです.中点の座標は,
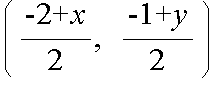
- となります.この点が直線 x + y + 1 = 0 上にあることより,その x,及び,y 座標を x + y + 1 = 0 に代入することによって,
x + y - 1 = 0
- という関係が得られます.また,線分 AB ( 傾きは,(y + 1) / (x + 2) )は直線 x + y + 1 = 0 (傾きは -1 )に直交していることにより,
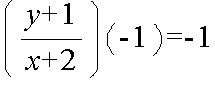
- が成立します.これらの関係より,点 B の座標は (0, 1),点 P の座標は (-1, 0) となります.
- 上の議論からも明らかなように,点 Q(x0, y0) から,直線 ax + by + c = 0 までの距離(点 Q から直線におろした垂線の長さ)は,以下のようにして計算できます.
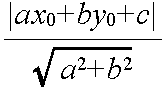
- たとえば,先の図における点 A から直線までの距離(線分 AP の長さ)は,以下のようになります.
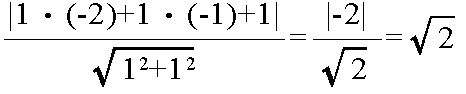
- 放物線の方程式
- 放物線は,一般に,以下のような式で表されます.
y = a (x - p)2 + q (1)
- 右辺の第 1 項は,a が正であれば常に 0 以上,a が 負であれば常に 0 以下となります.いずれの場合も,x = p のとき第 1 項が 0 になりますので,a の正負により,y の値は最小値 q,または,最大値 q となります.そして,この点が 2 次関数の頂点の座標 (p, q) になります.また,頂点を通る直線 x = p を軸といいます.なお,頂点に関しては,右下の図を参照して下さい.
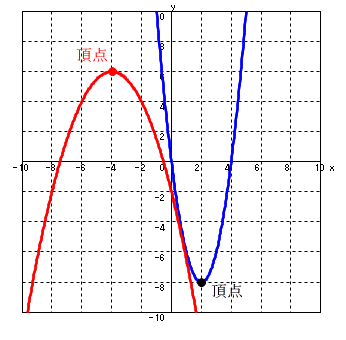
- 上図に示すのは,a が正,または,負となる場合に対する一つの例です.青色で描いたものは,関数,
y = 2 (x - 2)2 - 8 頂点:(2, -8), 軸:x = 2
- に対するグラフ,また,赤色で描いたものは,関数,
y = -0.5 (x + 4)2 + 6 頂点:(-4, 6), 軸:x = -4
- に対するグラフです.
- 2 次関数,
y = ax2 + bx + c (2)
- のグラフは,(2) 式を,以下に示すようにして,(1) 式の形に変換することによって容易に描くことができます.
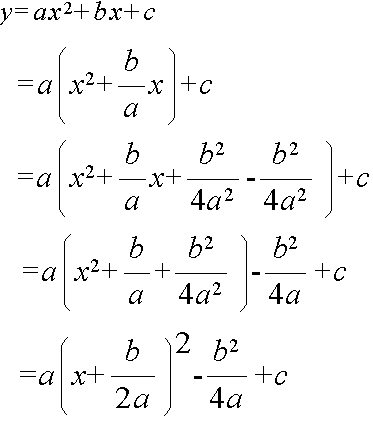
- たとえば,y = 2x2 - 4x + 4 は,以下のように変形できます.
y = 2(x - 1)2 + 2
- 放物線は,一般に,以下のような式で表されます.
- 放物線の方程式の決定
- 2 次関数には,3 つのパラメータがありますので,一般に 3 つの条件が与えられると,関数を一意に決定できます.たとえば,以下のような条件によって関数が決定します.
- 頂点の座標 (p1,q1) と通過する点 (x1, y1)
- 式 (1) において,頂点の座標から p1,q1 が決まり,通過する点の関係,
y1 = a (x1 - p1)2 + q1
- より,a を求める.
- 軸 x = p1 と通過する 2 点 (x1, y1),(x2, y2)
- 式 (1) において,軸の式から p1 が決まり,通過する点の関係,
y1 = a (x1 - p1)2 + q y2 = a (x2 - p1)2 + q
- より,q,a を求める.
- x 軸との交点 (x1, 0) と (x2, 0),及び,y 軸との交点 (0, y1)
- 式 (2) において,以下の関係,
0 = ax12 + bx1 + c 0 = ax22 + bx2 + c y1 = c
- より,a,b,c を求める.
- 通過する 3 点 (x1, y1),(x2, y2),(x3, y3)
- 式 (2) において,以下の関係,
y1 = ax12 + bx1 + c y2 = ax22 + bx2 + c y3 = ax32 + bx3 + c
- より,a,b,c を求める.
- 放物線の最大値と最小値
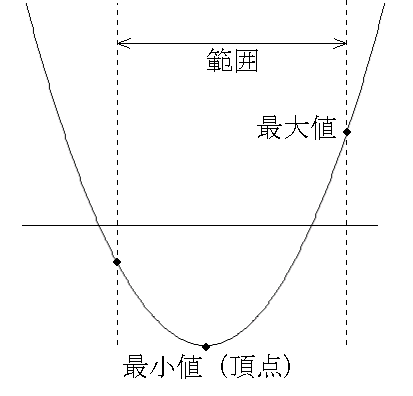
- x の範囲が指定されていない場合,
- a > 0 のとき: 頂点の y 座標が最小値となり,最大値は正の無限大
- a < 0 のとき: 頂点の y 座標が最大値となり,最小値は負の無限大
- となります.
- x の範囲が指定されている場合は,その範囲の両端,または,頂点の位置(頂点を範囲内に含む場合)で,最大値または最小値をとります(上図参照,a > 0 の場合).
- 円の方程式
- 中心が (a, b),半径が r の円の方程式は,
(x - a)2 + (y - b)2 = r2 (1)
- のように記述されます.たとえば,中心が (1, -2),半径が 3 の円の方程式は,
(x - 1)2 + (y + 2)2 = 9
- となり,そのグラフは下図のようになります.
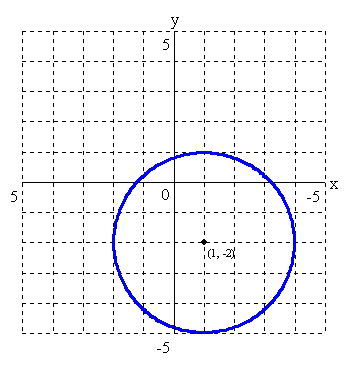
- (1) 式を展開すると,
x2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0
- のようになります.一般に,円の方程式は,
x2 + y2 + ex + fy + g = 0 (2) ただし,4g - e2 - f2 < 0
- のように記述できます.(2) 式から (1) 式へは,放物線の項で述べた方法と同様な方法で変換可能です.
- 円の接線
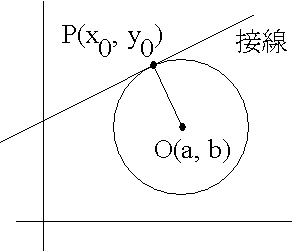
- 円 (x - a)2 + (y - b)2 = r2 の円周上の1点 P(x0, y0) における接線の方程式について考えてみます.「1次関数」の項で述べたように,1次関数は傾きと通る点によって一意に決定できます.上図に示すように,線分 OP と接線は直交しますので,
- (接線の傾き)×(線分 OP の傾き) = -1
- という関係があります.従って,上図のような場合は,線分 OP の傾きが (x0 - a) / (y0 - b) ですので,接線の傾きは,
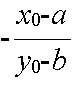
- となります.この傾きと,接線が点 P を通ることにより,接線の方程式は以下のようになります.
(x0 - a) (x - a) + (y0 - b) (y - b) = r2
- 円の方程式の決定
- 円の方程式には,3 つのパラメータがありますので,一般に 3 つの条件が与えられると,関数を一意に決定できます.たとえば,以下のような条件によって関数が決定します.
- 中心の座標と半径
- (1) 式から直接決まる
- 中心と通る点
- 中心から通る点までの距離から半径が決まる
- 中心と,x 軸または y 軸に接する情報
- 軸までの距離から半径が決まる
- 直径の両端の 2 点
- 2 点の中点より,半径と中心が決まる
- 1 次関数と 1 次方程式
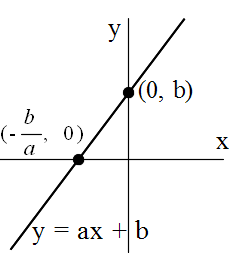
- 方程式と関数とは非常に深い関係があります.例えば.1 次方程式,
ax + b = 0 (1)
- の解は,上図に示すように,1 次関数,
y = ax + b
- の x 軸との交点の x 座標に相当します.
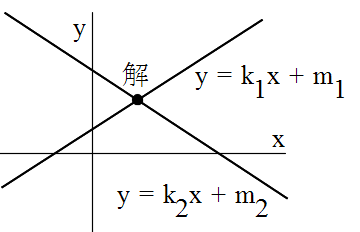
- また,2 つの直線が平行でないときは,必ずどこかで交わります.上図に示すように,この交点(共有点)が,連立方程式,
y = k1x + m1 y = k2x + m2
- の解になっていることに注意してください.このような意味から,1 次方程式 (1) の解は,2 つの直線,
y = ax + b y = 0
- の交点の x 座標であるともいえます.
- 2 次関数と 2 次方程式
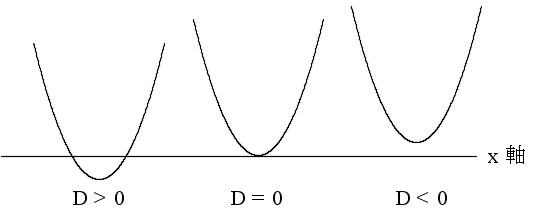
- 2 次方程式 ax2 + bx + c = 0 の解は,放物線 y = ax2 + bx + c と 直線 y = 0 ( x 軸)との交点の x 座標の値になります.判別式 D = b2 - 4ac の値が正,0,又は,負であることは,下の図( a > 0 の場合)に示すように,放物線が x 軸と交わる,接する,又は,交わらないということに相当します
- 上に述べた関係は,放物線 y = ax2 + bx + c と 1 次関数 y = dx + e との関係についても同様です.連立方程式
y = ax2 + bx + c> y = dx + e
- の解は,放物線と直線の交点の座標となります.従って,直線と放物線が共有点を持つか否かは判別式によって判定できます.例えば,上の 2 つの方程式から変数 y を消去すると,以下のようになります.
ax2 + bx + c = dx + e
- この方程式の解が共有点の x 座標となりますので,
(b - d)2 - 4a(c - e) > 0 : 放物線と直線が交わる (b - d)2 - 4a(c - e) = 0 : 直線が放物線に接する (b - d)2 - 4a(c - e) < 0 : 放物線と直線は交わらない
- となります.この関係は,放物線が円である場合も同様です.下の図は,上の 3 つが放物線と直線,また,下の 3 つが円と直線の関係を表しています.
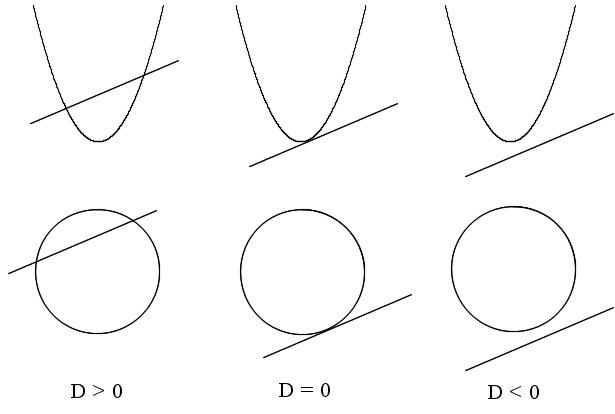
x + 3 > 0, x2 - 4 < 0
x > -3, -2 < x < 2
y > ax + b, y > ax2 + bx + c, (x - a)2 + (y - b)2 > r2
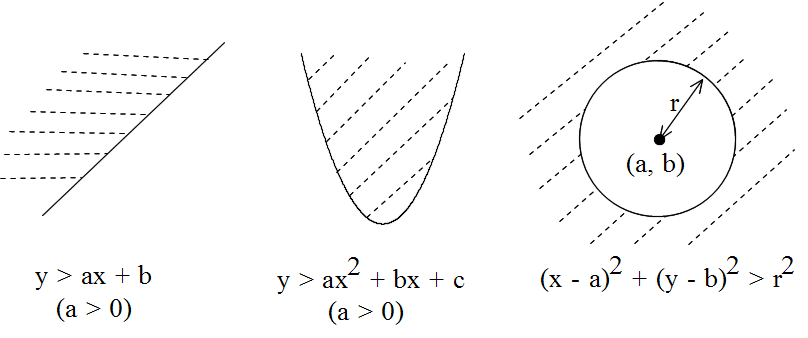
- 三角比の定義
- 右図に示すような直角三角形 ABC において,三角形の大きさによらず,角 α の大きさだけによって決まる正弦( sine ),余弦( cosine ),及び,正接( tangent )を以下のように定義し,これらを三角比と呼びます.
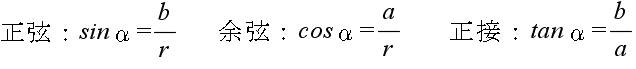
- 三角比は,上に示すような鋭角だけではなく,正負を含む,一般角に対しても定義できます.xy 座標平面上に原点 O を中心として,半径 r の円を描きます.その円周上に点 P をとり,OP と x 軸とのなす角度を θ とします.点 P の座標を ( x, y ),点 P から x 軸に垂線を下ろしその交点を Q とすると,点 Q の座標は ( x, 0 ) となります.このとき,各角度に対する三角比は以下のようになります.
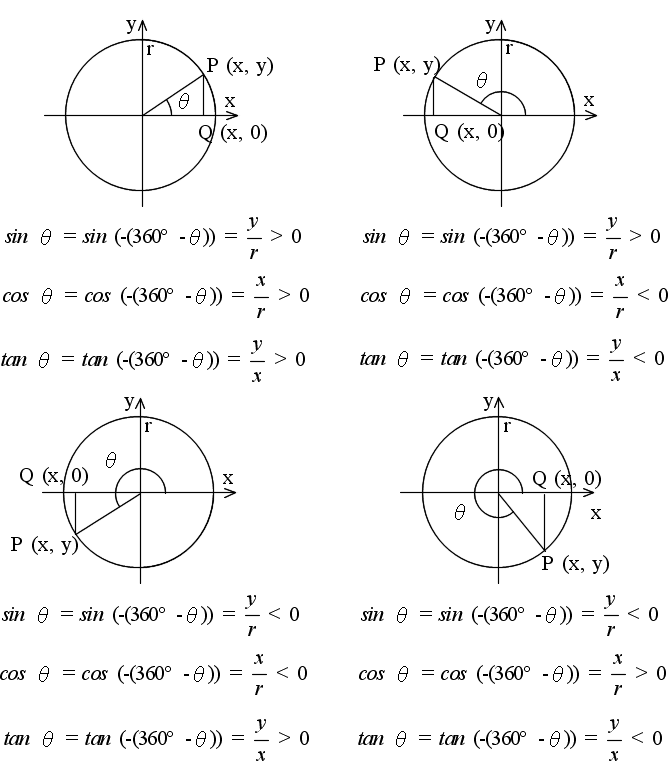
- 三角比の性質
- その定義や上の図からも明らかなように,三角比には,
- sin (0゜) = sin (360゜) = 0, cos (0゜) = cos (360゜) = 1, tan (0゜) = tan (360゜) = 0
- sin (90゜) = sin (-270゜) = 1, cos (90゜) = cos (-270゜) = 0, tan (90゜) = tan (270゜) = 定義できない
- sin (-90゜) = sin (270゜) = -1, cos (-90゜) = cos (270゜) = 0, tan (-90゜) = tan (270゜) = 定義できない
- sin (180゜) = sin (-180゜) = 0, cos (180゜) = cos (-180゜) = -1, tan (180゜) = tan (-180゜) = 0
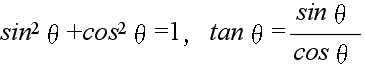
- sin (-θ) = -sin (θ), cos (-θ) = cos (θ)
- sin (90゜- θ) = cos (θ), cos (90゜- θ) = sin (θ)
- sin (90゜+ θ) = cos (θ), cos (90゜+ θ) = -sin (θ)
- sin (180゜- θ) = sin (θ), cos (180゜- θ) = -cos (θ)
- sin (180゜+ θ) = -sin (θ), cos (180゜+ θ) = -cos (θ)
- sin (n×360゜+ θ) = sin (θ), cos (n×360゜+ θ) = cos (θ) n = 0, ±1, ±2, ・・・
- のような関係が成立します.また,以下に示すように,30゜,45゜,および,60゜における三角比の値はよく使用されますので,理解し,記憶しておいてください.
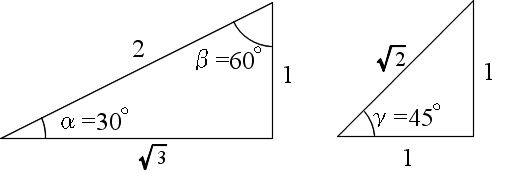
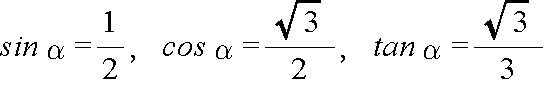
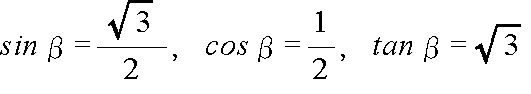
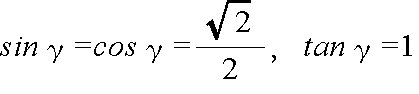
- 一般的に,任意の角度における三角比は表などによって知ることができますが,30゜,45゜,および,60゜における三角比や,上に示したような関係を利用して,以下の例に示すように,特定の角度における三角比を計算することができます.
- [例1] sin α = 0.1 のとき(ただし,0゜< α < 90゜),cos α や tan α は,以下のようにして計算できます.
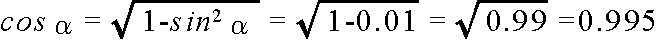
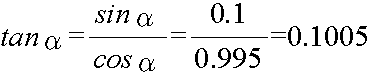
- [例2] sin (150゜) = sin (90゜+ 60゜) = cos 60゜ = 0.5
- 正弦定理と余弦定理
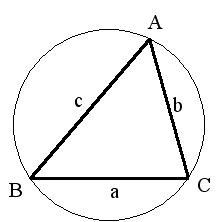
- 上図において( R: 三角形の外接円の半径),以下のような関係が成立します(正弦定理).
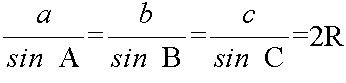
- また,△ABC の 1 つの角と 3 辺の長さの間には,次の関係が成立します(余弦定理)
a2 = b2 + c2 - 2bc cos A
b2 = c2 + a2 - 2ca cos B
c2 = a2 + b2 - 2ab cos C- [例3] 先の図において,a = 2,b = 3,c = 4 のとき,∠Aの大きさは,以下のようにして計算できます.
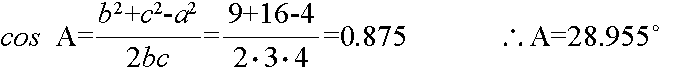
- 弧度法
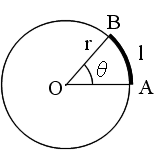
- 一般に,中心角 θ は円弧 AB の長さ l (エル)に比例します.また,円弧の長さ l と扇型の半径 r の比( l / r )をとると,円の大きさにかかわらず,同じ角度 θ に対してこの比は一定となります.そこで,この比によって角度の大きさを表す方法を弧度法と呼びます.単位はラジアン( rad )ですが,通常,単位名は省略します.
- 円の半径が 1 である場合は,l / r は円弧の長さに相当します.半径 1 の円周は 2π ですので,360°が 2π に相当します.従って,x°は,
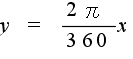
- ラジアンになります.
- 一般に,中心角 θ は円弧 AB の長さ l (エル)に比例します.また,円弧の長さ l と扇型の半径 r の比( l / r )をとると,円の大きさにかかわらず,同じ角度 θ に対してこの比は一定となります.そこで,この比によって角度の大きさを表す方法を弧度法と呼びます.単位はラジアン( rad )ですが,通常,単位名は省略します.
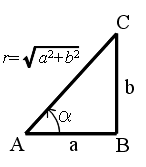
- 加法定理
- 角度の和や差に対して,以下の公式が成り立ちます(加法定理).
- sin(α + β) = sinα cosβ + cosα sinβ
- sin(α - β) = sinα cosβ - cosα sinβ
- cos(α + β) = cosα cosβ - sinα sinβ
- cos(α - β) = cosα cosβ + sinα sinβ
- 加法定理において,β = α と置くことによって,次の 倍角の公式が得られます.
- sin(2α) = 2 sinα cosβ
- cos(2α) = cos2α - sin2α = 1 - 2 sin2α = 2 cos2α - 1
- また,余弦に対する 2 倍角の公式から,次の半角の公式が得られます.
- 加法定理を使用して,以下に示すような,積を和・差になおす公式,及び,和・差を積に直す公式が得られます.
- また,加法定理を利用して,以下に示すように,a sin θ + b cos θ を r sin (θ + α) の形に変形できます.これを,三角関数の合成と呼びます.
- 三角関数のグラフ
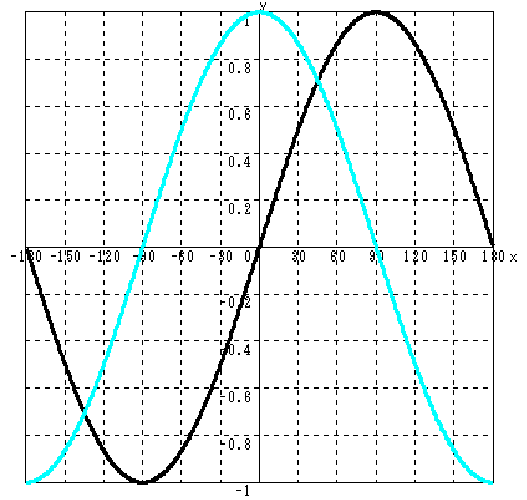
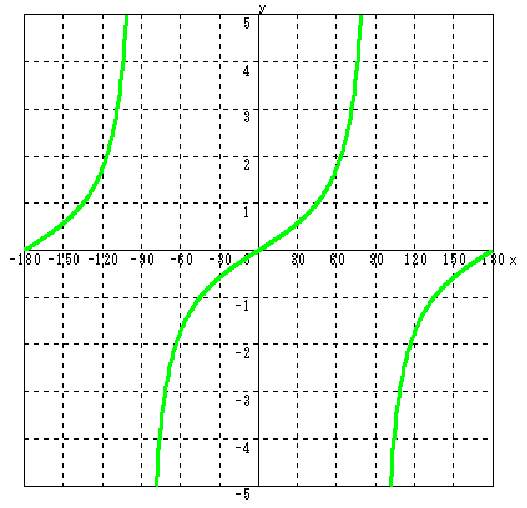
- 以下に,三角関数のグラフの例として,
- y = sin (x) (上のグラフの黒色)
- y = cos (x) (上のグラフの空色)
- y = tan (x) (下のグラフ)
- のグラフを示します.
xn = a
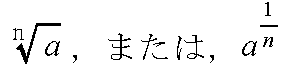
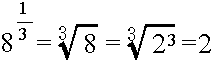
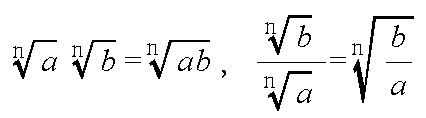
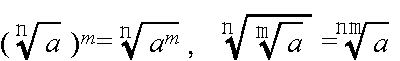
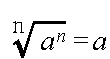
axay = ax + y, (ax)y = axy, (ab)x = axbx
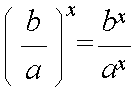
y = ax
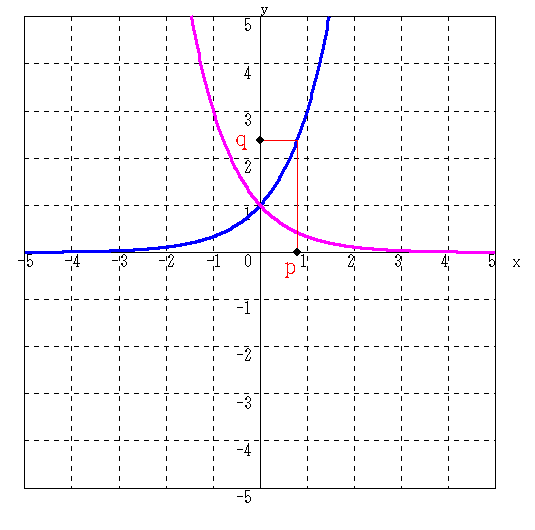
ap = q
p = logaq
log101000 = 3
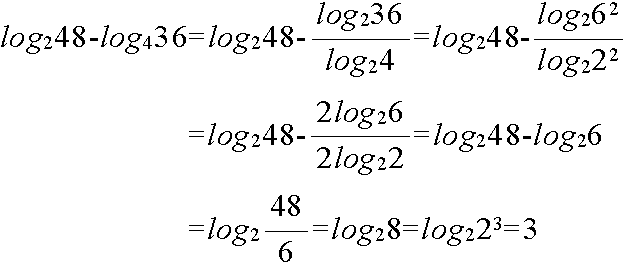
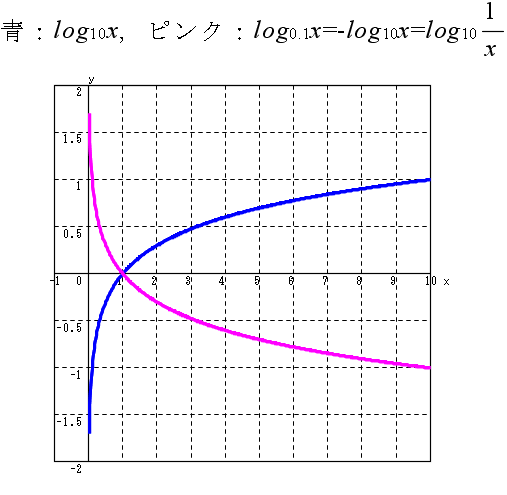
y = logax
3, 6, 9, 12, ・・・
a1, a2, a3, a4, ・・・, an, ・・・
an = 3n
an = a1 + (n - 1) d
Sn = a1 + (a1 + d) + (a1 + 2d) + ・・・ + {a1 + (n - 1)d}
Sn = {a1 + (n - 1)d} + {a1 + (n - 2)d} + {a1 + (n - 3)d} + ・・・ + a1 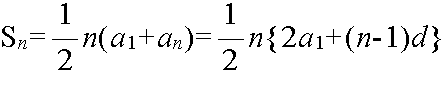
an = a1r(n - 1)
Sn = a1 + a1r + a1r2 + ・・・ + a1r(n - 1) (1)
rSn = a1r + a1r2 + a1r3 + ・・・ + a1rn (2)
(1 - r)Sn = a1 - a1rn