問題設定
- 配送問題とは,ある1カ所に設定された配送センターから,指定された複数の店舗に,できる限り少ないトラックで,かつ,各トラックはできる限り短い経路で配送する問題である.巡回セールスマン問題(Traveling Salesman Problem,以下TSPと略す)と似ているが,トラックの台数も決定しなければならないため,多少複雑な問題になる.
実際の問題においては,- 道路の存在
- 同じ距離であっても,時間帯,場所による移動時間の違い
- 荷物の積み卸し時間
- 荷物の積載量
- 配送時間の指定
- 等,多くの制約条件が関わってくるが,ここでは,計算時間の関係から,以下のように問題を単純化する.
- 評価関数
- f = wt0*tr + wt1*Σri (1) (和は,i=1,・・・,tr)
- を最小にするトラック台数及び各トラックの経路を見つける.ただし,
- tr:トラック台数
- ri:i番目のトラックの移動距離(配送センターから配送センターへ戻るまで)
- wt0,wt1:重み(100と1)
- とする.
- 配送センターはxy軸の原点にあり,配送先の店舗はx,y座標とも,±100の内部にランダムに配置されている.
- すべての店舗間を直接移動するための道が存在する.
- 各トラックの最大移動可能距離は345,また,1台のトラックの最大配送可能店舗数は20とする.
方法
- 遺伝的アルゴリズム
- 各個体の染色体は,荷物を配送すべき店舗番号の並びであり,配送する順序を表しているものとする.従って,遺伝子長は配送する店舗の数となり,外見上はTSPにおいてよく使用されるコーディング方法と同じである.しかし,このままでは,各トラックが配送する店舗及び必要なトラック数が不明であるので,それらを以下のような手順に従って決める.配送センターを出発した1台目のトラックは,染色体に記述された最初の店舗に向かい,順に,2番目,3番目の店舗に配送していくものとする.ただし,指定された移動可能最大距離の関係から次の店舗への配送が不可能な場合(配送センターへの戻るのに必要な距離も考慮)は,配送センターに戻り,次の店舗以降を2台目のトラックが配送することとする.この処理を配送すべき店舗がなくなるまで繰り返すことによって,必要なトラック台数及び各トラックの配送する店舗が決まることになる.
- GAは,初期集団を発生させた後,交叉,突然変異,適応度((1)式の符号を変えたもの)の計算,淘汰を繰り返して最適解を得ようとするものである.交叉方法としては,一様順序交叉,順序交叉,循環交叉,一様位置交叉,部分的交叉,サブツアー交叉を比較した結果,エッジ組み替え交叉を採用することとした.また,突然変異作用素として,ランダムに選ばれた2点間の遺伝子順序を逆に並べ替える方法(逆位),及び,ルーレット選択にエリート戦略を組み合わせた淘汰戦略を採用した.
- 反復改善法
- 反復改善法は,TSPに対する近似解法としてよく知られた方法である.TSPの一つの経路において,その中のλ本の枝を入れ換えて得られる経路の集合をλ近傍と呼ぶ.このλ近傍に含まれる経路の一つが,元の経路より短い経路であればそれに置き換え,再びそのλ近傍を考えるという手順を,改善が得られなくなるまで続ける方法である.
- ここでは,2近傍または3近傍(2近傍を含む)を利用した.経路の表現方法及びトラック台数の計算方法に関しては,GAにおける一つの染色体と全く同じである.
- マルチエージェントシステム
- マルチエージェント環境のもとで,以下に述べるような前提で,配送問題を解くことを試みる.
- 各トラックを自律したエージェントとみなす.
- 初期状態において,各トラックの配送すべき店舗は,各トラックの配送先店舗に重複がないという条件の下,最大配送可能店舗数の範囲内でランダムに決定する.したがって,すべての店舗をいずれかのトラックで1度だけ配送するという条件は満たされているが,トラックの台数(エージェントの数)は,乱数の初期値によって異なり,通常かなり大きな値となる.しかし,後に述べる交渉の結果,配送する店を他のエージェントに奪われ,配送する店をすべて失うような現象(エージェントの消滅)が発生することにより,徐々にエージェントの数は減少する.
- 各エージェントは,自分の配送する店舗に関する最適な経路を見つけることは可能であるが,全体システムに対する評価値を知ることはできない.
- 同時に交渉可能なのは,2つのエージェントだけである(交渉方法については後述).
- 以上述べた前提の元で,以下のようにして処理は進行する.
- 1台目のトラック(エージェント)が配送する店舗を,配送すべき全店舗リストの中から,ランダムに1つ選択し,その店舗を店舗リストから除く.同様の処理を,配送する店舗数が最大配送可能店舗数(20)になるか,または,配送するのに必要な移動距離が最大移動可能距離を超える直前まで続ける.1台目のトラックの配送先が決まると,2台目のトラックの配送先を同様の方法で決める.以上の処理を,配送すべき店舗リストが空になるまで続ける.
- エージェント毎に,3近傍を使用した反復改善法によって,経路の最適化を行う.このとき,交渉の指導権を持つエージェントを決定する資料とするため,各エージェントの強さを計算する.
- str=wt2*n_c+wt3*r 経路長が300以下
- =wt2*n_c+wt3*300+wt4*(r-300) 経路長が300以上
- ただし,
- n_c:各エージェントが配送する店舗の数
- r:各エージェントの経路長
- wt2,wt3,wt4:重み(1,0.03,及び,0.01)
- とする.
- ランダムに一つのエージェント(主体,交渉の指導権を持つ)を選ぶ
- ランダムに交渉相手を選ぶ.もし,相手を選ぶことに失敗すれば,Cに戻る.相手としては,必ず,主体が勝てるエージェントが選ばれる.2つのエージェント間の勝敗は,各エージェントの強さによって決まり,以下の3つの場合について検討する.
- 常に,強い方が勝つ.(強者戦略)
- 主体の強さをstr,相手の強さをo_strとしたとき,以下の式で計算される確率に従って決める.ただし,以下の値が0.1以下の時は0.1とする.(確率戦略)
- 0.5 + 1.0 * (str - o_str) / str (2)
- ランダムに決定する.(ランダム戦略)
- 選択された2つのエージェント間で交渉を行う.交渉結果として,勝者(主体)は,配送する店舗を相手と交換するか,または,相手から店舗を奪うことになる.交渉に関して,以下の3つの場合について検討する.なお,交渉が成立しなかった場合は,なにもせずCへ戻る.
- 相手の状況を無視する.つまり,交換等によって,相手の利益が損なわれても関知しない.店舗の交換による主体の経路長(強さ)の減少量が,店舗を奪うことによる強さの増加量より多ければ交換が選ばれ,逆ならば,店舗を奪うことになる.ただし,いずれの店舗の交換または奪取によっても主体の利益が得られなければ,交渉は成立しない.交換または奪取は,各店舗を1つずつチェックし,上で条件を満足する店舗を最初に見つけた時点で実行される.したがって,両エージェントが20店舗所有する場合は,最悪,20×20の組み合わせに対してチェックしなければならず,計算時間上,最も問題となる箇所となる.(無視戦略)
- 上とほぼ同じであるが,交換の場合は,相手の経路長も減少する場合にだけ交渉が成立する.(協調戦略)
- 交換するか,奪うか,また,どの店舗を対象にするかのすべてをランダムに決定する.(ランダム戦略)
- 交渉に携わった各エージェントの最適経路及び強さを再計算した後,Cへ戻る.
- 各個体の染色体は,荷物を配送すべき店舗番号の並びであり,配送する順序を表しているものとする.従って,遺伝子長は配送する店舗の数となり,外見上はTSPにおいてよく使用されるコーディング方法と同じである.しかし,このままでは,各トラックが配送する店舗及び必要なトラック数が不明であるので,それらを以下のような手順に従って決める.配送センターを出発した1台目のトラックは,染色体に記述された最初の店舗に向かい,順に,2番目,3番目の店舗に配送していくものとする.ただし,指定された移動可能最大距離の関係から次の店舗への配送が不可能な場合(配送センターへの戻るのに必要な距離も考慮)は,配送センターに戻り,次の店舗以降を2台目のトラックが配送することとする.この処理を配送すべき店舗がなくなるまで繰り返すことによって,必要なトラック台数及び各トラックの配送する店舗が決まることになる.
結果
表1 MASにおける交渉戦略による違い 勝敗
交渉
達成回数
車の台数
評価値
強者
無視
451.4
6.5
2573.6
協調
452.1
6.3
2546.0
確率
無視
2072.1
5.4
2190.8
協調
1873.5
5.3
2168.6
ランダム
無視
2535.8
6.0
2400.8
協調
2267.2
6.3
2478.0
ランダム
ランダム
2480.2
8.1
3189.3
- MAS(50店舗)において,勝敗及び交渉戦略を変えた場合に対する結果を表1に示す.試行回数(交渉回数)を3000回とした場合であり,比較のため,表の最下段には,勝敗及び店舗の交換・奪取をすべてランダムにした場合(偶然性による改善)の結果を示してある.これらの結果は,異なる10個(ただし,確率戦略に対しては30個)の乱数初期値に対する結果を平均したものであり,次節以下のシミュレーションにおいても同様である.
- 表1に示されるように,単に偶然性によって最適解が得られているわけでは無いことは明らかである.結果に大きな影響を与えるのは,勝敗に関する戦略の違いである.強者が必ず勝つような戦略をとると,ある特定な状態に素早く達した後は,ほとんど変化しなくなる(局所解に陥った状態).また,ランダム戦略を採用すると,収束も遅く,かつ,十分な結果も得られない.ほぼ予想されたように,上記二つの中間的な戦略である確率戦略が最も良好な結果を与えた.強いものだけではなく,弱いものも勝つ場合があるという戦略が,GAにおける突然変異の役割を果たしていることになる.もちろん,(2)式のパラメータや式自体を変更することによって得られる結果も異なってくるが,ここではそれらに対する詳細な検討は割愛する.図1は,各勝敗戦略による評価値の変化の状況を典型的な例で示したものである.また,図2は,50店舗に対する問題解決の例(初期状態と得られた最適な状態)を示したものである.
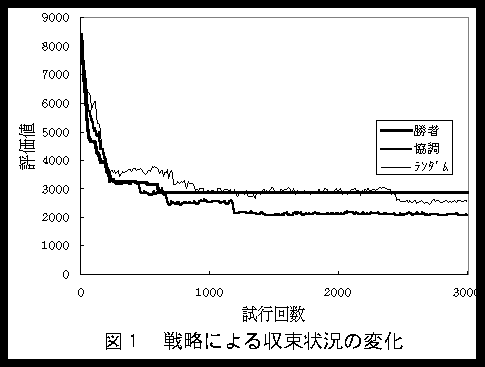
- 交渉戦略における協調と無視戦略間において,少なくとも表1の上ではあまり大きな差は認められない.協調戦略を採ると,勝者の意味が薄れると共に,交換する店舗の選択範囲が狭まり,勝敗戦略における強者戦略と同様に,局所的な最適値に留まってしまうことを予想したが,あまりそのような傾向は見られなかった.恐らく,本問題の場合には,奪取が常に相手の状態を無視して行われる点が大きく影響しているものと思われる.
- 表中に達成回数という項目がある.表に与えた車の台数や評価値(全体に対するもの)を達成した回数であるが,MASでは,当然,その回数以降,達成した評価値を維持していくわけではない(車の台数は維持される).全体の評価値を知らない各エージェント間で交渉を行っているため,評価値はかなり変動する.また,その評価値に達成するまでの過程においても,変動を繰り返すとともに,勝敗戦略によって大きく異なってくる(図1).


図2 50店舗に対する問題解決の例
- 表2は,GA,反復改善法,及び,MASを比較したものである.表中に示す最小値とは,異なる10個の乱数初期値に対応する各結果の内,最小となったものである.計算時間の関係上,500店舗の場合に対しては,GAは1ケース,3近傍反復改善法は2ケースの平均値をとった結果であり,また,2000店舗の場合(時間の都合上,20000回で終了させている)に対しては1ケースの値である.
- 店舗数が大きな場合に対し,真の最適値を得ることは非常に困難であり,表2においても,真の最適値を与えていない.そのため,得られた結果がどの程度妥当なものかを絶対的に判断することは困難である.しかし,ここでは,各車の配送可能店舗数を20に制限しているため,車の台数が(店舗数/20)より小さくなることはない.この点に注意をすれば,結果の妥当性に対するある程度の予想が可能である.
- GAにおいて,子供は各世代毎に集団サイズと同じ数だけ生成され,また,淘汰の際,エリートとして集団サイズの上位1割だけを次世代にそのまま残している.また,GAに対する表中の値は,集団の中で最適な適応度を持つ個体に対応するものである.少なくとも店舗数が100程度までは,他の方法と比較しても遜色の無い結果を与えている.集団サイズ,世代交代数等を増加させることによって,乱数の初期値によらず,より最適に近い値に収束させることもある程度可能である(もちろん,計算時間は増加する).しかしながら,店舗数が増加すると,計算時間は急激に増加し,たとえば,500店舗の場合でさえ,この程度の計算時間(集団サイズ,世代交代数等)では,十分満足する解を得ることができなかった.この表において,1000店舗以上に対する結果が与えてないのもこの理由による.
- 反復改善法は,計算時間の面からだけ見れば,最も優れた方法である.しかしながら,2近傍を利用した場合,すでに50店舗の場合に対してさえ,得られた結果はあまり好ましくなく,店舗数が多くなるほどその傾向は強くなる.従って,店舗数が非常に少ない場合に対してしか利用できない方法である.3近傍を利用した場合においても,店舗数が多くなれば解の品質が低下する点においては2近傍の場合と同様であるが,より多くの店舗数に対して適用可能である.少なくとも100店舗程度までは,計算時間,解の品質といった面から,最も良い方法であるといえる.しかし,500店舗に対する計算時間を見れば明らかなように,店舗数の増加に伴う計算時間の増大は急激である.3近傍を利用した場合,3つの枝を入れ換えてその結果を調べることになるが,最悪の場合,各段階で,nC3個のケース(nは店舗数)を調べなければならず,計算時間の面から,あまり大きな店舗数に対しては適用できない.
- MASにおいても,計算時間,解の品質といった面から,他の方法とほぼ同様の結果が得られた.3近傍を使用した反復改善法の特に最小値の項と比較しても明らかなように,解の品質といった面から言えば,全体の評価値を元に最適化を行っている他の方法と比べ劣っていると言える.GAの場合においては,集団サイズ,世代交代数を増加させることによって,表中に与えられた結果より好ましい値を得ることが可能である.しかし,MASの場合は,個々のエージェントが全体の評価値を知らないと言う前提があるため,勝敗や交渉の戦略にもよるが,少なくともここで与えたシステムでは,試行回数の増加だけでは解決できない問題である.
- しかしながら,計算時間の問題は重要である.確かに,MASにおいても,店舗数が増加すれば計算時間も増えるが,エージェントというサブシステムに分割されているため,その増加の程度が他の方法に比較して小さい.他の方法によってはほとんど実行不可能である1000店舗以上に対してさえ,表中に示されたような計算時間で,ある程度満足できる解が得られたことは注目すべき点である.
表2 各方法の比較 店舗数
10
20
50
100
500
1000
2000
GA
初期車台数
2.9
6.9
18.1
35.4
203.0
-
-
初期評価値
1099.5
2610.7
6858.6
13597.0
76283.0
-
-
集団サイズ
30
50
100
500
1000
-
-
世代交代数
200
1000
5000
10000
9000
-
-
車の台数
2.0
3.2
5.6
7.8
79.0
-
-
〃 (最小値)
2.0
3.0
5.0
7.0
79.0
-
-
評価値
814.3
1286.0
2206.8
3114.2
31757.0
-
-
〃 (最小値)
813.0
1236.0
2050.0
2883.0
31757.0
-
-
計算時間(分)
0.1
0.8
13.9
521.5
12103.0
-
-
反復
(2近傍)初期車台数
4.5
8.6
21.7
41.3
218.7
-
-
初期評価値
1557.0
3167.6
8068.9
15273.2
80838.1
-
-
達成回数
13.2
39.0
139.9
356.3
2335.8
-
-
車の台数
2.0
3.9
6.7
10.0
38.2
-
-
〃 (最小値)
2.0
3.0
6.0
8.0
34.0
-
-
評価値
814.5
1445.1
2553.5
3837.1
14687.4
-
-
〃 (最小値)
813.0
1237.0
2259.0
3146.0
13194.0
-
-
計算時間(分)
0.0
0.0
0.0
0.1
17.7
-
-
反復
(3近傍)初期車台数
4.5
8.6
21.7
41.3
218.7
-
-
初期評価値
1557.0
3167.6
8068.9
15273.2
80838.1
-
-
達成回数
10.5
41.2
151.1
423.4
3136.5
-
-
車の台数
2.0
3.2
5.7
7.8
26.0
-
-
〃 (最小値)
2.0
3.0
5.0
7.0
26.0
-
-
評価値
813.4
1289.9
2210.8
3065.6
9365.5
-
-
〃 (最小値)
813.0
1236.0
2034.0
2851.0
9310.0
-
-
計算時間(分)
0.0
0.0
0.1
2.1
8534.5
-
-
MAS
初期車台数
4.9
10.1
25.8
50.5
258.2
520.9
1042.0
初期評価値
1592.1
3255.9
8392.1
16627.8
84524.3
171165.7
340743.7
試行回数
200
1000
3000
5000
20000
50000
20000
車の台数
2.0
3.0
5.3
7.2
27.2
53.7
156.0
〃 (最小値)
2.0
3.0
5.0
7.0
27.0
53.0
156.0
評価値
813.8
1238.9
2168.6
3001.9
11425.2
22584.3
66258.6
〃 (最小値)
813.0
1236.0
2043.0
2906.0
11276.0
22217.0
66258.6
計算時間(分)
0.1
0.5
15.5
605.1
1481.4
4329.1
15362.0
- 配送問題とは,ある1カ所に設定された配送センターから,指定された複数の店舗に,できる限り少ないトラックで,かつ,各トラックはできる限り短い経路で配送する問題である.巡回セールスマン問題(Traveling Salesman Problem,以下TSPと略す)と似ているが,トラックの台数も決定しなければならないため,多少複雑な問題になる.