情報学部 菅沼ホーム

マルチエージェント手法によるＴＳＰの解法

  1. はじめに

    　　巡回セールスマン問題（TSP）に対して，遺伝的アルゴリズム（GA），Simulated Annealing，Elastic Net，Self-Organizing Map，さらには，蟻の社会を模擬したシステム等，数多くの方法が提案され，高い精度の解が得られている．しかしながら，それらの方法の多くは，

    1. 乱数を使用した探索を基本としているため，同じ問題に対して，複数回の試行を行わなければならない．
    2. 実行パラメータの調整が必要である．

    等の問題を持っており，規模が大きい問題に対しては，かなりの実行時間がかかることを覚悟しなければならない．

    　　そこで，本論文においては，乱数，および，都市の数と各都市の座標以外一切のパラメータを使用せず，１回の試行だけで常に同じ近似解が得られる方法を提案する．また，この方法は，マルチエージェントを利用しているため（以後，この方法をMAM -Multiagent Method- と略す），並列処理が可能であれば，さらに高速に近似解を求めることが可能となる．

    　　TSPに代表される組み合わせ最適化問題は，その規模が大きくなると解を求めるのが非常に困難となる．おそらく，唯一の解決手段は並列的な処理であろう．最近，複数のエージェントが協調しながら問題を解決するシステムに対する研究が多くの分野で注目を集めている．各エージェントの行動を並列的に処理することによって，大規模システムに対する高速処理が期待できる．問題は，各エージェントにどのような役割を持たせ，また，どのような協調動作を行わせるかといった点である．蟻の社会を模擬したシステムのように，各エージェントに独立に全体の問題を解かせ，より精度の高い解を得るために協力するといった方法も一つの方法であるが，規模の拡大による直接的な影響を受けやすい．

    　　これを避ける可能性がある手段として，問題を副問題に分割し，各副問題を異なるエージェントに処理させる方法が考えられる．しかし，この方法には，「どのように問題を分割するのか」，「各エージェント間の協調をどのように制御するのか」，「各副問題の解を全体の解にどのように結びつけるのか」等といった困難な問題が多い．TSPに対する近似解法として知られている分割法も，マルチエージェントシステムの一種とみなせるが，同様の問題を抱えている．また，乱数を使用するため，同じ状況に対して複数回の処理が必要となる．

    　　本論文で提案するMAMは，分割法の一種とみなすこともできる．ただし，分割法のように，分割方法を考慮したり，また，各領域で得られた解をどのように結合すべきかといった点について検討する必要は全くない．また，経路を徐々に延ばしていくと言った面からみると，Elastic Netによる方法に似ているが，本方法では乱数や複雑なパラメータ設定を全く必要としない．詳細については後述するが，MAMは，複数のエージェントを発生させ，それらのエージェントが分裂を繰り返しながら解を求めようとするものである．

    　　残念ながら，MAM単独では，十分の精度の解を得ることができない．そこで，次に，MAMとGAの結合について検討する．TSPに対してGAを利用した例は多いが，その最も大きな問題点は，染色体に個体のすべての情報，つまり，都市を訪れる完全な順番を保存していることにあると思われる．生命体でいえば，生命体を構成する各細胞の種類やそのつながり方を，染色体上に完全な状態で保存していることに相当する．その膨大な情報を遺伝的操作によって改善しようとするため，都市数が多くなると単純な遺伝操作で解を見つけることが困難になり，他の近傍探索手法と同時に使用したり，または，交叉や突然変異の方法に工夫を凝らしている場合が多い．

    　　しかしながら，基本的な細胞分裂方法と細胞分裂をコントロールする制御規則を要所要所で与えることによって生命体を完成させることが可能であれば，制御規則だけを遺伝情報として次世代に受け渡してやればよく，染色体上に記述される遺伝情報は非常に少なくなるはずである．このことにより，単純な遺伝操作と少ない世代数による個体の改善が期待できる．本論文では，この考え方に従って，GAとMAMを組み合わせることを試みる．

    　

  2. 基本的方法（MAM）

    1. アルゴリズム

      　(a)　 　(b)　 　(c)　 　(d)　 　(e)　 　(f)　 　(g)　

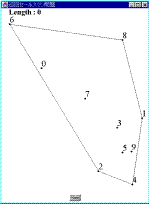
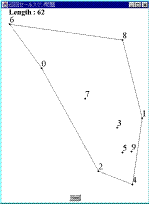
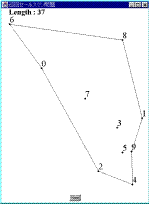
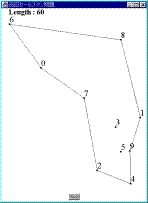
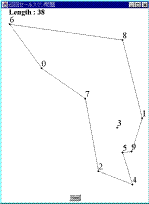
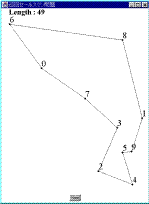
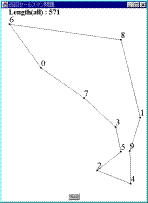
      Fig.1 解が得られる過程

      　　MMAは，以下に示すアルゴリズムに従って実行される．

      1. 凸多角形の生成
        　　すべての都市をその内部に含み，辺の数が最小の凸多角形を生成する．この多角形の各頂点は，問題を構成するいずれかの都市である必要がある．Fig.1は，本論文で提案する方法によって解が形成されていく過程を表しているが，Fig.1(a)がその凸多角形を示している．なお，Fig.1において，各点は都市であり，そこに示された数字は都市番号を表している．以後，この多角形を構成する辺をエージェントと呼ぶ．Fig.1(a)の例では，5つのエージェント（6-2，2-4，4-1，1-8，8-6）が存在することになる．

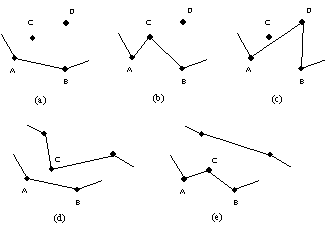        Fig.2 エージェントの分裂

      2. 分裂対象都市の計算
        　　各エージェント毎に，分裂対象都市を選択する．分裂対象都市とは以下に示すような都市である．たとえば，Fig.2(a)に示すように，エージェントA-Bと，エージェントを構成しない都市C，Dがあったとする．このとき，エージェントA-Bは，都市CまたはDを吸収し，エージェントA-CとC-D（Fig.2(b)），または，A-DとD-B（Fig.2(c)）に分裂することになる．これらの都市の内，距離の増加（たとえば，A-C＋C-D－A-B）が最小のものを，エージェントA-Bの分裂対象都市とする．Fig.2(a)では，都市CがエージェントA-Bの分裂対象都市となる．
        　　分裂対象都市として，すでに他のエージェントを構成している都市も対象とする場合がある．たとえば，Fig.2(d)のように，都市CをエージェントA-Bが吸収して，Fig.2(e)のようになった方が対象とする部分の距離が短くなる場合である．Fig.1の例では，(f)から(g)への変化がそれに対応する．

      3. エージェントの分裂
        　　すべてのエージェントの内，距離の増加が最も少ないものを選び，そのエージェントを分裂させる．この結果，エージェントを構成しない都市が0になれば終了し，そうでなければ，(2)へ戻る．

      　　上に述べた処理において，最も時間がかかるのは，(2)の処理であるが，可能ならば，各エージェント毎に並列的に実行可能な部分でもある．

    2. 実行結果

      　　実行結果をTable 1のMAMの欄に示す（問題のアルファベットの後ろの数字は都市数）．問題は，TSPLIB：http://softlib.rice.edu/softlib/tsplib/から，各都市の座標が２次元ユークリッド空間の座標として整数で与えられているものを採用した．MAMは，問題の影響をかなり強く受けると思われるため，できるだけ多くの問題に対して適用してみた．ただし，メモリ上の制約から，都市数が極端に多い問題は実行できなかった．また，他の方法と比較する際における実行時間上の制約より，都市数が多い問題の一部は省略してある．Table 1において，bestおよびtimeは，最良値の誤差及びその値を得るためにかかった計算時間である（0は，1秒未満であることを示す）．なお，実行は，pentiumⅢ1GHzを搭載したパソコン上で，gccを使って行った（ただし，Fig.1に示すように，実行過程を描画するためには，Java JDK1.2を使用した）．

      Table 1 MAM，3-opt，および，分割法の比較
      problem optimum MAM 3-opt partition
      　 　 best(%) time(sec) best(%) count time(sec) average(%) best(%) count time(sec) average(%) part
      eil51 426 2.58 0 0.00 1 0 2.35 0.00 1 0 2.35 1x1
      berlin52 7542 5.94 0 0.00 10 0 4.42 0.00 10 0 4.42 1x1
      st70 675 2.67 0 0.00 2 1 2.22 0.00 2 1 2.22 1x1
      eil76 538 5.20 0 0.93 1 1 3.35 0.93 1 1 3.35 1x1
      pr76 108159 4.90 0 0.00 3 2 1.76 0.00 3 2 1.76 1x1
      rat99 1211 0.50 0 1.07 1 2 4.13 1.07 1 2 4.13 1x1
      kroA100 21282 2.57 0 0.00 2 3 2.52 0.00 2 3 2.52 1x1
      kroB100 22141 2.60 0 0.26 1 4 2.25 0.26 1 4 2.25 1x1
      kroC100 20749 1.53 0 0.10 2 3 3.05 0.10 2 3 3.05 1x1
      kroD100 21294 1.42 0 0.00 1 3 3.19 0.00 1 3 3.19 1x1
      kroE100 22068 2.14 0 0.21 1 4 2.15 0.21 1 4 2.15 1x1
      eil101 629 5.09 0 1.27 2 3 3.50 1.27 2 3 3.50 1x1
      lin105 14379 0.38 0 0.00 4 4 2.07 0.00 4 4 2.07 1x1
      pr107 44303 2.77 0 0.19 1 4 0.91 0.19 1 4 0.91 1x1
      pr124 59030 1.89 0 0.00 4 6 1.23 0.00 4 6 1.23 1x1
      bier127 118282 2.57 0 0.58 1 9 2.49 0.58 1 9 2.49 1x1
      pr136 96772 1.72 0 0.68 1 16 4.19 0.68 1 16 4.19 1x1
      pr144 58537 2.34 0 0.00 8 8 0.67 0.00 8 8 0.67 1x1
      kroA150 26524 5.17 1 0.22 1 15 2.93 0.22 1 15 2.93 1x1
      kroB150 26130 2.98 0 0.53 1 20 2.18 0.53 1 20 2.18 1x1
      pr152 73682 1.25 0 0.18 3 12 1.60 0.18 3 12 1.60 1x1
      u159 42080 10.24 0 0.00 2 25 4.02 0.00 2 25 4.02 1x1
      rat195 2323 6.63 0 2.50 1 42 4.69 2.50 1 42 4.69 1x1
      kroA200 29368 5.42 1 0.43 1 39 3.61 1.39 1 7 3.79 2x1
      kroB200 29437 5.78 0 1.52 1 57 4.07 1.79 1 6 4.03 2x1
      ts225 126643 19.00 1 0.00 2 111 3.49 3.37 1 5 6.64 1x2
      pr226 80369 1.87 1 0.40 1 105 2.16 3.60 1 9 5.85 2x1
      gil262 2378 8.75 1 2.31 1 142 3.99 3.36 1 14 5.21 1x2
      pr264 49135 3.58 1 0.78 1 179 5.45 2.28 1 60 8.26 1x2
      a280 2579 3.37 2 2.52 1 175 6.48 3.88 1 23 7.48 2x1
      pr299 48191 4.68 2 1.72 1 299 4.18 1.38 1 30 3.91 2x1
      lin318 42029 7.74 2 1.57 1 445 3.74 3.64 1 10 5.72 1x3
      pr439 107217 4.83 6 1.83 1 2062 5.10 7.66 1 18 9.52 3x3
      pcb442 50778 7.24 3 2.89 1 2210 4.57 3.70 1 70 5.22 1x3
      u574 36905 6.39 8 - - - - 4.77 1 66 6.14 4x1
      rat575 6773 6.32 10 - - - - 4.22 1 157 5.52 1x3
      u724 41910 6.41 15 - - - - 5.62 1 58 7.53 3x2
      rat783 8806 7.27 24 - - - - 4.93 1 57 6.63 2x3
      pr1002 259045 6.32 46 - - - - 6.48 1 49 7.82 3x3
      u1060 224094 7.93 69 - - - - 6.00 1 48 7.72 4x3
      vm1084 239297 8.78 62 - - - - 5.34 1 60 6.62 4x3
      nrw1379 56638 6.04 114 - - - - 6.27 1 88 6.93 6x3
      vm1748 336556 9.40 253 - - - - 8.50 1 89 9.16 5x4
      rl1889 316536 10.60 561 - - - - 8.51 1 99 10.32 4x4
      u2319 234256 3.28 1043 - - - - 2.10 1 339 2.48 13x1
      pr2392 378032 8.67 1117 - - - - 5.58 1 274 6.59 4x4
      pcb3038 137694 7.45 1432 - - - - 6.31 1 268 7.12 8x3
      　 max 19.00 　 2.89 　 　 6.48 8.51 　 　 10.32 　
      　 average 5.15 　 0.73 　 　 3.20 2.54 　 　 4.64 　

      　　参考のため，近傍探索手法としてよく使われている3近傍を利用した逐次改善法（3-optの欄），および，都市数が多い問題にも適用可能な分割法（partitionの欄）と比較してみる．逐次改善法に対しては，乱数を変え50試行を行い，その最良値と平均値の誤差（bestとaverage）を記載してある．countは，50回の試行の内，最良値を得られた回数である．

      　　分割法に関しては，領域をl（l＝n×m．水平方向をn等分，かつ，垂直方向をm等分）分割し，やはり50試行行った結果である（各領域の最適化は，3-optで行っている）．ただし，分割方法によって解が異なるため，各領域に入る最大都市数が200未満の分割から，徐々に分割数を増やしていき，最大都市数が100未満になるまでのすべての分割の内，最適な分割方法を選択した．この分割方法が，partitionの欄に記載してある．同じ分割数でも，nとmの値により，分割方法が異なるため，それらすべての場合に対して検討した（ただし，都市数が200未満の問題に対しては，1分割の結果であり，3-optの結果と同じである）．

      　　比較対象とした二つの方法とも，最近報告されている多くの方法に比べれば，精度的にかなり劣っている．MAMは，これら二つの方法に比較してさえ，良好な結果が得られているとは言えない．せいぜい，都市数が大きな問題に対しては，ほぼ分割法の平均値レベルの精度であると言える程度である．しかしながら，表に記載されている結果を求めるためには，分割法の場合，表に与えた計算時間の（試行回数×分割方法）倍の時間が必要であることを考慮すると，MAMには，近似解を素早く求める一つの手法としての役割はあるのではないであろうか．

  3. ＧＡの利用

    1. 方法

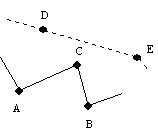      Fig.3 不適当な分裂

      　　なぜ，MAMは最適な解を求めることができないのであろうか．一言でいえば，大域的な視点で判断を行っていないということに尽きる．大域的な視点に立っていないがために生じる結果として，たとえば，Fig.3に示すような場合について考えてみる．もし，点線で示すように都市DとEがエージェントを構成していれば，都市CはエージェントD-Eの分裂対象都市になるはずである．しかし，まだエージェントを構成していないため，エージェントA-Bの分裂対象都市になってしまう．この影響が一つの都市だけの範囲で終われば，3.1節(2)の後半の部分で述べた方法により，エージェントD-Eが生成された後であっても，修復することが可能である．しかし，一般には，連鎖反応的に他の都市にも影響を与え，修復が不可能になることが多い．

      　　アルゴリズム上では，2.1節(3)で述べた分裂させるエージェントを選択する順序の問題である．その後の展開を考慮すると，必ずしも距離の増加が最小のエージェントを分裂させることが最適であるとは限らない．したがって，そのような場合だけ，別のエージェントを分裂させるような規則を付加できれば，最適な解が得られるはずである．実際，Table 1にあげた問題の内，eil51とkroA100に対して，１ステップずつ実行しながら，そのような制御を行ってみた．その結果，いずれの問題とも，10カ所程度で標準以外のエージェントを分裂させることによって最適解を得ることができた．

      　　しかしながら，「一般的に規則をどのようにして記述するか」，また，「その規則をどのようにして得るか」等，問題は多い．本論文では，明示的な規則という形ではなく，別の形で規則に相当するものを表現してみる．たとえば，Fig.3で示した例の場合，最初の段階では都市Cが存在せず，エージェントD-Eが生成された後，都市Cを出現させれば問題ないはずである（もちろん，エージェントA-Bの分裂対象都市として都市DやEが選ばれた場合，距離の増加量が他のエージェントにおける増加量より大きい必要がある）．そこで，2.1節で述べたアルゴリズムに以下の機能を付加する．

      付加手続き　凸多角形が生成された後，エージェントを構成しない都市の内，n個だけを対象に(2)および(3)の手続きを繰り返す．n個の都市がすべてエージェントに組み込まれた後，残りの都市の内，別のn個を対象に同じ手続きを繰り返す．同様の手続きを繰り返し，すべての都市がエージェントを構成した時点で終了する．

      　　この方法により，Fig.3の例であれば，都市Cが，エージェントD-Eが生成された後のn個のグループに入っていれば，正しい分裂が起こるはずである．さらに，必ずしも2.1節で述べた凸多角形の状態から開始する必要もない．ランダムに選ばれたk個の都市からなる経路を，凸多角形と同等のものとみなして，以後の手続きを行っても解は得られるはずである．このとき，k個の都市を結ぶ経路は，k個の都市だけを対象として，2.1節で述べた方法によって求めるものとする．

      　　しかし，どのようなグループに分け，どのような順序で処理するかによって，大きく結果は異なってくる．一つの方法は，様々なパラメータに対し，乱数を使用し，多くの試行を実行した後，最適なものを選ぶ方法である．しかし，偶然性に頼るため，かなり多くの試行を必要とする可能性がある．参考のため，eil51とkroB100に対して実行した結果をTable 2に示す．Table 2において，nの値はグループの大きさを示し，また，kの値は最初にランダムに選ばれる都市の数を示す．ただし，kの値が0の欄は，2.1節の方法の通り，全体の都市を対象とした凸多角形から開始した場合である．bestとaverageの欄は，50回の試行で得られた最良値と平均値の誤差である．この表からも明らかなように，この程度の問題でさえ，最適値を得ることは困難である．

      Table 2 初期状態，及び，グループ数を変えた結果
      　 k 0 5 10 15 20
      problem n best(%) average(%) best(%) average(%) best(%) average(%) best(%) average(%) best(%) average(%)
      eil51 5 1.41 3.29 0.70 3.05 1.17 3.05 1.17 3.29 0.70 3.29
      　 10 0.23 3.29 1.41 3.05 1.64 3.52 0.70 3.05 0.70 3.29
      　 15 0.23 3.29 1.41 3.29 1.64 3.52 0.70 3.29 0.23 3.29
      　 20 0.23 3.52 0.70 3.52 0.94 3.05 0.70 3.52 0.23 3.29
      kroB100 5 0.87 4.19 1.59 4.15 1.58 4.22 1.58 4.18 1.58 4.05
      　 10 1.37 4.10 1.17 3.93 1.91 4.41 1.17 4.01 1.91 4.12
      　 15 1.75 4.02 1.57 4.23 1.57 4.05 1.91 4.18 1.17 3.84
      　 20 1.88 4.44 2.15 4.54 1.57 4.40 1.87 4.25 1.75 4.21
      　 30 1.75 4.06 1.29 4.34 1.66 4.58 1.07 4.50 1.75 4.20
      　 40 1.33 3.99 1.81 4.99 1.17 4.55 1.92 4.65 2.21 4.40

      　　そこで，GAを利用してこの問題を扱うことにする．Table 2からも明らかなように，グループの大きさnも結果に大きな影響を与えるが，実行時間の都合上，本論文では，n＝10に固定する．GAを用いたアルゴリズムは以下に示す通りである．

      1. 初期集団の発生　集団サイズは都市数の10の位を四捨五入した後，10で割った値とする（たとえば，都市数が51の問題eil51で10，都市数が442の問題pcb442で40となる）．各個体の染色体は，都市の並びであるが，凸多角形の頂点を構成する都市が常に最初に来るようにしてある（数は，問題によって一定：m）．それ以後の都市は，10個ずつが一つのグループとして取り扱われる．

      2. 適応度の計算　各染色体に表現されている都市の並びは都市を訪れる順序ではないため，各個体は，2.1節に述べたアルゴリズムに付加手続きを加えた方法によって，実際に実行してみる必要がある．したがって，染色体が都市を訪れる順番で記述されている方法に比べてかなりの実行時間がかかることになる．さらに，付加手続きにより，グループを加える毎に初期設定的な処理を行わなければならず，2.1節だけの方法に比べ，都市数に比例した時間がかかる．
        　　交叉と突然変異によって生成された個体では，染色体の最初のm個の都市が，2.1節で述べた凸多角形を構成する都市になるとは限らない．そのような場合，先に述べたように，最初のm個の都市を対象として，2.1節で述べた手続きを行い，それを凸多角形に対応する初期状態とする．

      3. 交叉　交叉方法としては，一様順序交叉を採用した．一様順序交叉とは，位置の集合をランダムに選択し，一方の親の選択された位置における遺伝子の順序に従って，他の親の遺伝子を並べ替えたものを子にする方法である．子供の数は集団サイズと同じとする．

      4. 突然変異　突然変異方法として，転座を採用する．転座とは，２点間の遺伝子を他の位置のものと置き換える方法である．本論文における方法においては，同じグループ内に入っている都市の順番が，染色体上で変化しても，個体の適応度には全く影響を与えない．そのため，交叉だけを使用した場合，かなり早い世代に，すべての適応度が等しくなってしまう．そこで，変則的ではあるが，突然変異率を大きく（0.45）してこの現象を防いでいる．

      5. (5)淘汰　淘汰方法としては，ルーレット選択を採用している．ただし，最も適応度が高い個体1つだけは，次世代に残し，(2)へ戻る．

    2. 実行結果

      　　実行結果をTable 3に示す．best，time，および，gen.の欄は，それぞれ，最良値の誤差，その値を得るまでにかかった計算時間，および，そのときの世代である．前節で述べたように，個体の評価に時間がかかるため，並列処理ができないパソコン上では，かなり制限された状態で実行せざるを得なかった．すべての問題に対して，同じ乱数の初期値でただ1試行だけ実行し，かつ，200世代で計算を打ち切っている．また，前節で述べたように，個体サイズや子供の数もできるだけ押さえてある．表からも明らかなように，都市数が大きな問題に対しては，以上の設定では不十分であると思われる．また，さらに都市数の多い問題は，実行時間上の問題より割愛した．

      Table 3 MAM＋GA
      problem best(%) time(sec) gen.
      eil51 0.00 5 38
      berlin52 0.00 1 1
      st70 0.59 1 3
      eil76 0.00 27 53
      pr76 0.00 13 25
      rat99 0.00 52 44
      kroA100 0.00 1 1
      kroB100 0.26 26 22
      kroC100 0.00 10 9
      kroD100 0.00 81 68
      kroE100 0.05 219 187
      eil101 0.00 234 177
      lin105 0.00 10 8
      pr107 0.00 71 47
      pr124 0.00 155 64
      bier127 0.32 530 185
      pr136 0.09 521 158
      pr144 0.00 118 29
      kroA150 0.00 1287 134
      kroB150 0.02 570 64
      pr152 0.00 20 2
      u159 0.00 154 13
      rat195 2.07 1045 43
      kroA200 0.68 2576 104
      kroB200 0.06 4379 168
      ts225 0.50 1410 36
      pr226 0.00 5687 144
      gil262 0.71 12407 120
      pr264 0.80 8623 81
      a280 1.98 22728 177
      pr299 0.47 24262 146
      lin318 1.01 40227 197
      pr439 1.86 183025 194
      pcb442 2.57 183686 192
      max 2.57 　 　
      average 0.41 　 　

      　　他の論文と比較しうる都市数の問題に対して十分な結果が得られていないため，この時点で，MAMとGAを組み合わせた方法の優位性を主張することは困難である．しかし，都市数の少ない問題を見る限り，単純な交叉方法，および，かなり少ない個体数・子供の数・世代数によって，それなりの結果が得られていると言って良いのではなかろうか．少なくとも，通常の方法のように都市の訪問順序自体を染色体上に表現した場合，上で述べた実行条件内でTable 3程度の解を得ることはほとんど不可能である．
    　

  4. まとめ

    　　2.1節で述べた方法においては，距離の増加が最も少ないエージェントを分裂させるように設定したが，別の指標を設定することによって，より精度の高い解を得られる可能性も残っている．しかしながら，大域的な視点を一つの指標で完全に表現することは非常に困難であり，より精度の高い解を要求するならば，本論文のように，GAなどを併用せざるを得ないであろう．

    　　GAを使用する際，本論文においては，分裂順序を制御する明示的な規則を使用せず，多少変則的ではあるが，都市をグループに分けて分裂順序を制御するという方法を採用した．そのため，染色体表現の中に冗長な情報が含まれることになった（同じグループに属する都市の順番を変えても適応度は変化しない）．このことは，交叉や突然変異が有効に働くことを拒み，突然変異率を非常に大きくせざるを得なかった原因にもなっているものと思われる．

    　　この問題を解決するためには，交叉や突然変異方法を工夫することも一つの方法であるが，より適切なコーディング方法，つまり，制御規則を明示的に適切な形で表現し，それをGAによって獲得できるようにする必要があるものと思われる．それが可能であれば，TSPに限らず，大規模な問題に対して，GAをより有効に利用できるようになるのではないであろうか．

情報学部 菅沼ホーム