動的計画法（プログラム例）

1. 資源配分問題（0-1 ナップザック問題）ー投資先（品物）毎のデータを出力したい場合ー
2. 資源配分問題（0-1 ナップザック問題）ー投資先（品物）毎のデータを必要としない場合ー
3. 0-1 ナップザック問題 ー品物毎のデータを出力したい場合ー
4. 0-1 ナップザック問題 ー品物毎のデータを必要としない場合ー
5. グラフにおける最短距離問題 ー経路を出力したい場合ー
6. グラフにおける最短距離問題 ー経路を出力する必要が無い場合ー

　　動的計画法は，システムを複数の状態で表現し，初期状態から目標状態まで遷移させていき，その過程を通して最大値（最小値）を求めようとするものです．右図に示すように，ステップ (k+1) の状態 j におけるコストは，ステップ k の各状態におけるコスト（ステップ k に至るまでのコストの和）に，その状態からステップ (k+1) の状態 j に遷移（全ての状態から遷移できるとは限らない）するためにかかるコストを加えたものの内最小（最大）のものになります．これを，初期状態から目標状態まで繰り返せば解が得られます．ステップ (k+1) におけるコストは，ステップ k のコストだけで決まるため，最小（最大）を求めることだけが目的であれば，前後する 2 つのステップにおける状態だけを記憶しておけば良いことになります．

１．資源配分問題（0-1 ナップザック問題）ー投資先（品物）毎のデータを出力したい場合ー

　　資源配分問題は，n_toshi 種類の投資先に，max_t 単位の資金を配分し（資金は単位でしか配分できない），利益を最大にしようとするものです．このプログラム例では，以下に示すように（コメント部分は除く），n_toshi，及び，max_t の値と，各投資先に 1 から max_t 単位の資金を投資した場合に得られる利益を入力すれば結果を得ることができます．

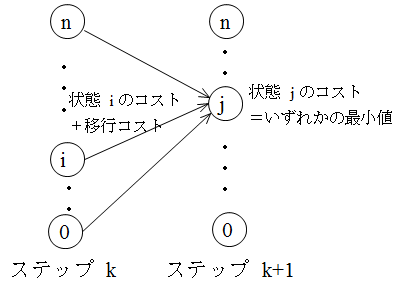
n_toshi max_t
p1,1 p1,2 ･･･ p1,max_t   // 1 番目の投資先によって得られる利益
p2,1 p2,2 ･･･ p2,max_t   // 2 番目の投資先によって得られる利益
　　・・・
pn_toshi,1 pn_toshi,2 ･･･ pn_toshi,max_t		

具体的には，例えば，投資先が 3，資金が 4 の場合，以下のようになります（コメント部分は除く）．

3 4
8 18 22 24   // 1 番目の投資先に 1 単位投資するとその利益は 8，2 単位投資するとその利益は 18，・・・
3 6 9 12   // 2 番目の投資先に 1 単位投資するとその利益は 3，2 単位投資するとその利益は 6，・・・
6 7 8 10   // ・・・		

　　資源配分問題においては，投資資金が状態になります（ 0 の場合も含めるため，状態数は (max_t+1) 個）．プログラムの table[i][j] には，ステップ (i+1) において j 単位の資金を投資した場合の利益が記憶されます．また，各投資先に対する投資額も知りたい場合には，table[i-1][k] から table[i][j] に遷移するする際，どの状態（ k の値）から遷移する際に table[i][j] が最大になるかを記憶しておく必要があります．これを行うのが，変数 prev です．

　　0-1 ナップザック問題も，データを適切に記述すれば，同じプログラムで解くことが可能です．0-1 ナップザック問題では，n_toshi 種類の品物からいくつか選んでをナップザックに入れるものとします．各品物を入れることによって，その品物固有の効用が得られます．ただし，ナップザックに入れることができる最大重量は max_t であり，この条件のもとで効用が最大になるように入れる品物を選ぶことになります．例えば，品物の数が 4，最大重量が 6 の場合，以下に示すような入力データになります（コメント部分は除く）．なお，0-1 ナップザック問題においては，ナップザック内に入っている品物の重量が状態になります．

4 6
2 0 0 0 0 0   // 1 番目の品物の重さは 1 で，その効用は 2
0 0 5 0 0 0   // 2 番目の品物の重さは 3 で，その効用は 5
0 0 4 0 0 0   // 3 番目の品物の重さは 3 で，その効用は 4
0 0 3 0 0 0   // 4 番目の品物の重さは 3 で，その効用は 3		

#**************************************************/
# 動的計画法：資源配分問題（0-1 ナップザック問題）*/
# ー投資先（品物）毎のデータを出力したい場合ー    */
#      coded by Y.Suganuma                        */
#**************************************************/
			# データの入力と領域の確保
a       = (gets().strip()).split()
n_toshi = Integer(a[0])   # 投資先数（品物数）
max_t   = Integer(a[1])   # 最大投資額（最大重量）
max_t  += 1   # 投資を行わない（品物を入れない）場合を含めるため
table   = Array.new(n_toshi)   # 投資額と利益（重さと効用）
rieki   = Array.new(n_toshi)   # 投資した際の利益（品物を入れた際の効用）
prev    = Array.new(n_toshi)   # 前段までの投資額（前段までの重さ）
for i1 in Range.new(0, n_toshi, true)
	table[i1] = Array.new(max_t)
	rieki[i1] = Array.new(max_t)
	prev[i1]  = Array.new(max_t)
end
for i1 in Range.new(0, n_toshi, true)
	table[i1][0] = 0
	a             = (gets().strip()).split()
	for i2 in Range.new(1, max_t, true)
		table[i1][i2] = Integer(a[i2-1])
	end
end
			# 動的計画法
				# 初期設定（1段目）
for i1 in Range.new(0, max_t, true)
	rieki[0][i1] = table[0][i1]
	prev[0][i1]  = -1
end
				# 2段目以降
for i1 in Range.new(1, n_toshi, true)
	for i2 in Range.new(0, max_t, true)
		rieki[i1][i2] = rieki[i1-1][i2]
		prev[i1][i1]  = prev[i1-1][i2]
	end
	for i2 in Range.new(0, max_t, true)
		i3 = 0
		while i2+i3 < max_t
			if rieki[i1-1][i3]+table[i1][i2] > rieki[i1][i2+i3]
				rieki[i1][i2+i3] = rieki[i1-1][i3]+table[i1][i2]
				prev[i1][i2+i3]  = i3
			end
			i3 += 1
		end
	end
end
			# 結果の出力
k   = -1
max = -1
for i1 in Range.new(0, max_t, true)
	if rieki[n_toshi-1][i1] > max
		max = rieki[n_toshi-1][i1]
		k   = i1
	end
end
printf("最大利益（最大効用） %d\n", max)

#i1 = n_toshi-1
#while i1 > 0
for i1 in Range.new(n_toshi-1, 0, true).step(-1)
	k1 = 0
	if rieki[i1][k] != rieki[i1-1][k]
		k1 = k - prev[i1][k]
		k  = prev[i1][k]
	end
	printf("   投資先（品物） %d 投資単位（重さ） %d 利益（効用） %d\n", (i1+1), k1, table[i1][k1])
#	i1 -= 1
end
printf("   投資先（品物） 1 投資単位（重さ） %d 利益（効用） %d\n", k, table[0][k])
		

２．資源配分問題（0-1 ナップザック問題）ー投資先（品物）毎のデータを必要としない場合ー

　　資源配分問題（0-1 ナップザック問題）において，最大利益（最大効用）だけを知りたい場合には，table[i-1][k] から table[i][j] に遷移するする際，どの状態（ k の値）から遷移する際に table[i][j] が最大になるかを記憶する必要がありませんので，変数 prev は不必要です．また，前後 2 つのステップにおける状態だけを記憶しておけば良いので，変数 rieki の配列サイズを小さくすることができます．

#**************************************************/
# 動的計画法：資源配分問題（0-1 ナップザック問題）*/
# ー投資先（品物）毎のデータを必要としない場合ー  */
#      coded by Y.Suganuma                        */
#**************************************************/
			# データの入力と領域の確保
a       = (gets().strip()).split()
n_toshi = Integer(a[0])   # 投資先数（品物数）
max_t   = Integer(a[1])   # 最大投資額（最大重量）
max_t  += 1   # 投資を行わない（品物を入れない）場合を含めるため
table   = Array.new(n_toshi)   # 投資額と利益（重さと効用）
rieki   = Array.new(2)   # 投資した際の利益（品物を入れた際の効用）
for i1 in Range.new(0, n_toshi, true)
	table[i1] = Array.new(max_t)
end
for i1 in Range.new(0, 2, true)
	rieki[i1] = Array.new(max_t)
end
for i1 in Range.new(0, n_toshi, true)
	table[i1][0] = 0
	a             = (gets().strip()).split()
	for i2 in Range.new(1, max_t, true)
		table[i1][i2] = Integer(a[i2-1])
	end
end
			# 動的計画法
				# 初期設定（1段目）
k1 = 0
k2 = 1
for i1 in Range.new(0, max_t, true)
	rieki[0][i1] = table[0][i1]
	rieki[1][i1] = 0
end
				# 2段目以降
for i1 in Range.new(1, n_toshi, true)
	for i2 in Range.new(0, max_t, true)
		rieki[k2][i2] = rieki[k1][i2]
	end
	for i2 in Range.new(0, max_t, true)
		i3 = 0
		while i2+i3 < max_t
			if rieki[k1][i3]+table[i1][i2] > rieki[k2][i2+i3]
				rieki[k2][i2+i3] = rieki[k1][i3]+table[i1][i2]
			end
			i3 += 1
		end
	end
	k1 += 1
	k1 %= 2
	k2 += 1
	k2 %= 2
end
			# 結果の出力
max = -1
for i1 in Range.new(0, max_t, true)
	if rieki[k1][i1] > max
		max = rieki[k1][i1]
	end
end
printf("最大利益（最大効用） %d\n", max)
		

３．0-1 ナップザック問題 ー品物毎のデータを出力したい場合ー

　　0-1 ナップザック問題を資源配分問題に対するプログラムで解く場合，上の例で示したように，入力データとして余分な 0 を記述する必要があります．しかし，一般的には，以下に示すように，品物の数 N，ナップザックに入れることができる最大重量 W，及び，各品物の重さ w_i と その効用 v_i を入力するだけで十分です（コメント部分は除く）．

N W
w1 v1   // 1 番目の品物の重さとそれを入れた場合の効用
w2 v2   // 2 番目の品物の重さとそれを入れた場合の効用
　　・・・
wN vN		

例えば，先に挙げた例の場合，以下のようになります．

4 6
1 2
3 5
3 4
3 3		

#**************************************/
# 動的計画法（0-1ナップザック問題）   */
# ー品物毎のデータを出力したい場合ー  */
#      coded by Y.Suganuma            */
#**************************************/
			# データの入力と領域の確保
a = (gets().strip()).split()
N = Integer(a[0])   # 品物の数
W = Integer(a[1])   # 重さの上限
w = Array.new(N)   # 各品物の重さ
v = Array.new(N)   # 各品物の効用
for i1 in Range.new(0, N, true)
	a     = (gets().strip()).split()
	w[i1] = Integer(a[0])
	v[i1] = Integer(a[1])
end
			# 動的計画法
				# 初期設定（1段目）
prev = Array.new(N)   # 前段までの品物の重さ
dp   = Array.new(N)   # ナップザック内の品物の重さ
for i1 in Range.new(0, N, true)
	prev[i1] = Array.new(W+1)
	dp[i1]   = Array.new(W+1)
end
for i1 in Range.new(0, W+1, true)
	dp[0][i1]   = -1
	prev[0][i1] = -1
end
if w[0] <= W
	dp[0][w[0]] = v[0]
end
				# 2段目以降
for i1 in Range.new(1, N, true)
	for wt in Range.new(0, W+1, true)
		dp[i1][wt]   = dp[i1-1][wt]
		prev[i1][wt] = prev[i1-1][wt]
	end
					# 最初の品物である場合
	if w[i1] <= W and dp[i1][w[i1]] < v[i1]
		dp[i1][w[i1]]   = v[i1]
		prev[i1][w[i1]] = 0
	end
					# 過去に品物が入っている場合
	for wt in Range.new(1, W+1, true)
		if dp[i1-1][wt] > 0 and wt+w[i1] <= W
			if dp[i1-1][wt]+v[i1] > dp[i1][wt+w[i1]]
				dp[i1][wt+w[i1]]   = dp[i1-1][wt] + v[i1]
				prev[i1][wt+w[i1]] = wt
			end
		end
	end
end
			# 結果の出力
k   = -1
ans = -1
for i1 in Range.new(0, W+1, true)
	if dp[N-1][i1] > ans
		ans = dp[N-1][i1]
		k   = i1
	end
end
printf("最大効用　%d\n", ans)

for i1 in Range.new(N-1, 0).step(-1)
	k1 = 0
	if dp[i1][k] != dp[i1-1][k]
		k1 = k - prev[i1][k]
		k  = prev[i1][k]
	end
	vv = v[i1]
	if k1 <= 0
		vv = 0
	end
	printf("   品物 %d 重さ %d 効用 %d\n", (i1+1), k1, vv)
end
vv = v[0]
if k <= 0
	vv = 0
end
printf("   品物 1 重さ %d 効用 %d\n", k, vv)
		

４．0-1 ナップザック問題 ー品物毎のデータを必要としない場合ー

　　資源配分問題と同様，最大効用だけを知りたい場合には，プログラムはより簡単になります．

#****************************************/
# 動的計画法（0-1ナップザック問題）     */
# ー品物毎のデータを必要としない場合ー  */
#      coded by Y.Suganuma              */
#****************************************/
			# データの入力と領域の確保
a = (gets().strip()).split()
N = Integer(a[0])   # 品物の数
W = Integer(a[1])   # 重さの上限
w = Array.new(N)   # 各品物の重さ
v = Array.new(N)   # 各品物の効用
for i1 in Range.new(0, N, true)
	a     = (gets().strip()).split()
	w[i1] = Integer(a[0])
	v[i1] = Integer(a[1])
end
			# 動的計画法
				# 初期設定（1段目）
dp = Array.new(2)   # ナップザック内の品物の重さ
for i1 in Range.new(0, 2, true)
	dp[i1] = Array.new(W+1)
end
for i1 in Range.new(0, W+1, true)
	dp[0][i1] = -1
	dp[1][i1] = -1
end
if w[0] <= W
	dp[0][w[0]] = v[0]
end
k1 = 0
k2 = 1
				# 2段目以降
for i1 in Range.new(1, N, true)
	for wt in Range.new(0, W+1, true)
		dp[k2][wt] = dp[k1][wt]
	end
					# 最初の品物である場合
	if w[i1] <= W and dp[k2][w[i1]] < v[i1]
		dp[k2][w[i1]] = v[i1]
	end
					# 過去に品物が入っている場合
	for wt in Range.new(1, W+1, true)
		if dp[k1][wt] > 0 and wt+w[i1] <= W
			if dp[k1][wt]+v[i1] > dp[k2][wt+w[i1]]
				dp[k2][wt+w[i1]] = dp[k1][wt] + v[i1]
			end
		end
	end
	k1 += 1
	k1 %= 2
	k2 += 1
	k2 %= 2
end
			# 結果の出力
ans = 0
for i1 in Range.new(0, W+1, true)
	if dp[k1][i1] > ans
		ans = dp[k1][i1]
	end
end
printf("最大効用　%d\n", ans)
		

５．グラフにおける最短距離問題 ー経路を出力したい場合ー

　　ここでは，グラフにおける最短経路問題を扱います．初期ノードから目標ノードに至る最短経路を求める問題です．最短経路問題において，状態はノードとなりますので，状態の数はノードの数となります．例えば，右図に示すグラフにおいては，状態の数は 7 となり，ノード 0 から ノード 6 に至る最短経路を求めることになります．また，右図における枝上に記述された数字はノード間の距離を示しており，最短経路は赤で示した経路になります．このプログラムに対しては，以下に示すようなデータを入力します（コメント部分は除く）．

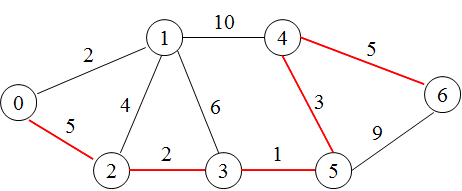
N M   // ノードの数，接続データの数（接続データが無いノード間は移動できない）
ni nj rij   // ノード ni と ノード nj 間の距離は rij
　　・・・		

例えば，上に示した図に対する入力データは以下のようになります．

7 10
0 1 2
0 2 5
1 2 4
1 3 6
1 4 10
2 3 2
3 5 1
4 5 3
4 6 5
5 6 9
		

#******************************************/
# 動的計画法（グラフにおける最短距離問題）*/
# ー経路を出力したい場合ー                */
#      coded by Y.Suganuma                */
#******************************************/
			# データの入力と領域の確保
a = (gets().strip()).split()
N = Integer(a[0])   # ノードの数
M = Integer(a[1])   # 接続状況データ数
r = Array.new(N)   # ノード間の距離
for i1 in Range.new(0, N, true)
	r[i1] = Array.new(N)
	for i2 in Range.new(0, N, true)
		r[i1][i2] = 0
	end
end
for i1 in Range.new(0, M, true)
	a         = (gets().strip()).split()
	k1        = Integer(a[0])
	k2        = Integer(a[1])
	r[k1][k2] = Integer(a[2])
end
for i1 in Range.new(0, N-1, true)
	for i2 in Range.new(i1+1, N, true)
		r[i2][i1] = r[i1][i2]
	end
end
			# 動的計画法
				# 初期設定（1段目）
prev = Array.new(N)   # 前のノード
dp   = Array.new(N)   # ノードへ達するまでの距離
for i1 in Range.new(0, N, true)
	prev[i1] = Array.new(N)
	dp[i1]   = Array.new(N)
	for i2 in Range.new(0, N, true)
		prev[i1][i2] = -1
		dp[i1][i2]   = -1
	end
end
dp[0][0] = 0
				# 2段目以降
n  = 0
sw = 1
while sw > 0
	sw = 0
	for i1 in Range.new(0, N, true)
		dp[n+1][i1]   = dp[n][i1]
		prev[n+1][i1] = prev[n][i1]
	end
	for i1 in Range.new(0, N, true)
		for i2 in Range.new(0, N, true)
			if dp[n][i1] >= 0 and r[i1][i2] > 0
				if dp[n+1][i2] < 0 or (dp[n][i1]+r[i1][i2] < dp[n+1][i2])
					dp[n+1][i2]   = dp[n][i1] + r[i1][i2]
					prev[n+1][i2] = i1
					sw            = 1
				end
			end
		end
	end
	if sw > 0
		n += 1
	end
end
			# 結果の出力
printf("最短距離　%d\n", dp[n][N-1])

k = N - 1
printf("   ノード番号 %d\n", k)
while n > 0
	printf("   ノード番号 %d\n", prev[n][k])
	k  = prev[n][k]
	n -= 1
end
		

６．グラフにおける最短距離問題 ー経路を出力する必要が無い場合ー

　　上のプログラムでは最短経路も出力されますが，このプログラムでは，最短経路長だけが出力されます．

#******************************************/
# 動的計画法（グラフにおける最短距離問題）*/
# ー経路を出力する必要が無い場合ー        */
#      coded by Y.Suganuma                */
#******************************************/
			# データの入力と領域の確保
a = (gets().strip()).split()
N = Integer(a[0])   # ノードの数
M = Integer(a[1])   # 接続状況データ数
r = Array.new(N)   # ノード間の距離
for i1 in Range.new(0, N, true)
	r[i1] = Array.new(N)
	for i2 in Range.new(0, N, true)
		r[i1][i2] = 0
	end
end
for i1 in Range.new(0, M, true)
	a         = (gets().strip()).split()
	k1        = Integer(a[0])
	k2        = Integer(a[1])
	r[k1][k2] = Integer(a[2])
end
for i1 in Range.new(0, N-1, true)
	for i2 in Range.new(i1+1, N, true)
		r[i2][i1] = r[i1][i2]
	end
end
			# 動的計画法
				# 初期設定（1段目）
dp = Array.new(2)   # ノードへ達するまでの距離
for i1 in Range.new(0, 2, true)
	dp[i1] = Array.new(N)
	for i2 in Range.new(0, N, true)
		dp[i1][i2] = -1
	end
end
dp[0][0] = 0
				# 2段目以降
sw = 1
k1 = 0
k2 = 1
while sw > 0
	sw = 0
	for i1 in Range.new(0, N, true)
		dp[k2][i1]   = dp[k1][i1]
	end
	for i1 in Range.new(0, N, true)
		for i2 in Range.new(0, N, true)
			if dp[k1][i1] >= 0 and r[i1][i2] > 0
				if dp[k2][i2] < 0 or (dp[k1][i1]+r[i1][i2] < dp[k2][i2])
					dp[k2][i2] = dp[k1][i1] + r[i1][i2]
					sw         = 1
				end
			end
		end
	end
	if sw > 0
		k1 += 1
		k1 %= 2
		k2 += 1
		k2 %= 2
	end
end
			# 結果の出力
printf("最短距離　%d\n", dp[k1][N-1])