プログラムの使用方法

　　提示したプログラムは，以下に示す 3 つの関数の最小値を最急降下法によって求めるためのものです．なお，各関数の解近傍における外形については，このページの最後に添付した図をご覧下さい．

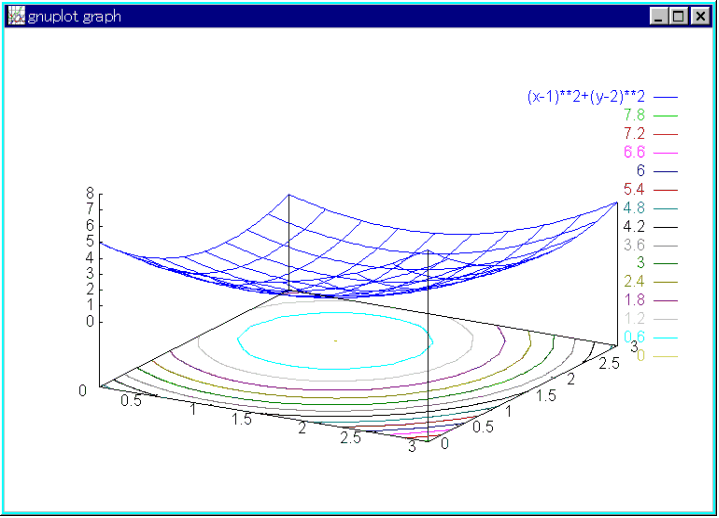
    1. f = (x - 1)2 + (y - 2)2　　最小値：(1,2) で 0.0
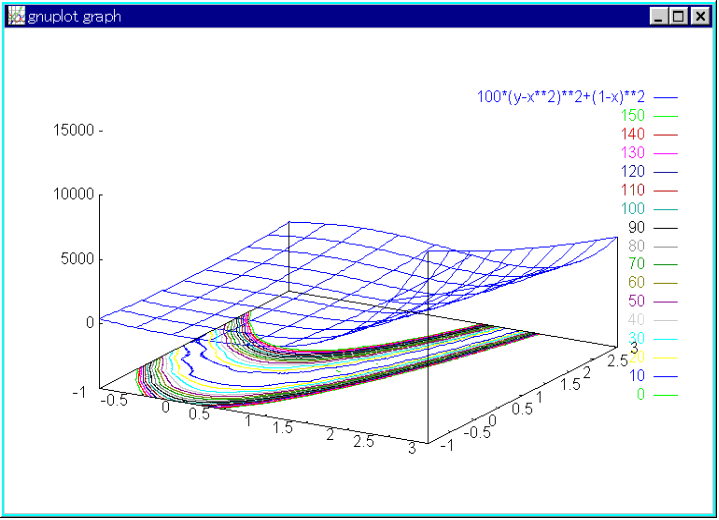
    2. f = 100(y - x2)2 + (1 - x)2　　最小値：(1,1) で 0.0
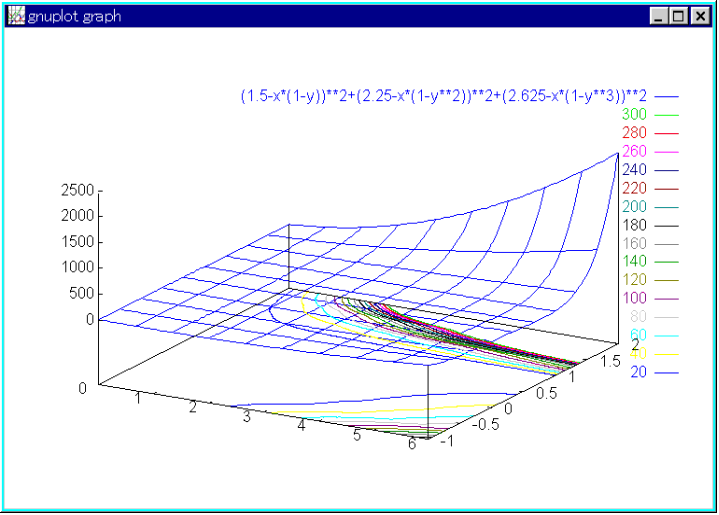
    3. f = (1.5 - x(1 - y))2 + (2.25 - x(1 - y2))2 + (2.625 - x(1 - y3))2　　最小値：(3,0.5) で 0.0

下に述べる入力データ記述ファイル data を適当に修正し，コマンドラインから， 
test < data   // C/C++，C#，VB の場合
Java Test < data   // Java の場合
PHP test.php < data   // PHP の場合
Ruby test.rb < data   // Ruby の場合
py -3 test.py < data   // Python の場合
などと入力してやることによって実行できます．また，< の前までを入力した後，ファイル data の内容をコピーし，画面に貼り付けても実行可能です．

　　入力データ記述ファイル data は，例えば，以下のように記述します． 
関数 1 変数の数 2 最大試行回数 100 一次元最適化 0
許容誤差 1.0e-10 刻み幅 0.5
初期値 0.0 0.0
上に示した各データにおいて，日本語の部分は次に続くデータの説明になっていますので，数字の部分だけを修正してください．日本語の部分を変更しても構いませんが，削除したり，間に半角のスペースを入れるようなことはしないでください．各データの意味は以下に示す通りです．

関数 1　　対象とする関数を指定します．上述の a，b，及び，c の各関数に対応し，1，2，または，3 を入力します．

変数の数 2　　変数の数を入力します．現在の例では，すべての関数に対して 2 となります．

最大試行回数 100　　最大試行（繰り返し）回数を入力します．

一次元最適化 0　　歩み幅α(k)を１次元最適化によって求めるか否かを入力します．0 を入力すると歩み幅α(k)を一定とし，また，1 を入力すると黄金分割法によってα(k)を決めます．

許容誤差 1.0e-10　　収束判定用の許容誤差です．

刻み幅 0.5　　歩み幅を入力します．歩み幅α(k)を１次元最適化によって求める場合は，初期歩み幅となります．

初期値 0.0 0.0　　各変数の初期値です．変数の数だけ（現在の例では 2）必要になります．

　　なお，各関数に対する入力例は以下に示すとおりです（ // を含む行はコメントであり，入力してはいけない）． 
					// 関数 a，一次元最適化を使用しない
関数 1 変数の数 2 最大試行回数 100 一次元最適化 0
許容誤差 1.0e-10 刻み幅 0.5
初期値 0.0 0.0
					// 関数 a，一次元最適化を使用する
関数 1 変数の数 2 最大試行回数 100 一次元最適化 1
許容誤差 1.0e-10 刻み幅 0.5
初期値 0.0 0.0
					// 関数 b，一次元最適化を使用しない
関数 2 変数の数 2 最大試行回数 10000 一次元最適化 0
許容誤差 1.0e-10 刻み幅 0.002
初期値 0.0 0.0
					// 関数 b，一次元最適化を使用する
関数 2 変数の数 2 最大試行回数 10000 一次元最適化 1
許容誤差 1.0e-10 刻み幅 0.002
初期値 0.0 0.0
					// 関数 c，一次元最適化を使用しない
関数 3 変数の数 2 最大試行回数 1000 一次元最適化 0
許容誤差 1.0e-10 刻み幅 0.04
初期値 0.0 0.0
					// 関数 c，一次元最適化を使用する
関数 3 変数の数 2 最大試行回数 200 一次元最適化 1
許容誤差 1.0e-10 刻み幅 0.04
初期値 0.0 0.0